No CrossRef data available.
Article contents
Flat sets
Published online by Cambridge University Press: 12 March 2014
Abstract
Let X be a set, and let 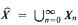 be the superstructure of X, where X0 = X and
be the superstructure of X, where X0 = X and 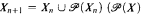 is the power set of X) for n ∈ ω. The set X is called a flat set if and only if
is the power set of X) for n ∈ ω. The set X is called a flat set if and only if 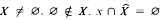 for each x ∈ X, and x ∩ ŷ = ø for x, y ∈ X such that x ≠ y. where
for each x ∈ X, and x ∩ ŷ = ø for x, y ∈ X such that x ≠ y. where  is the superstructure of y. In this article, it is shown that there exists a bijection of any nonempty set onto a flat set. Also, if
is the superstructure of y. In this article, it is shown that there exists a bijection of any nonempty set onto a flat set. Also, if 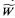 is an ultrapower of
is an ultrapower of 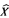 (generated by any infinite set I and any nonprincipal ultrafilter on I), it is shown that
(generated by any infinite set I and any nonprincipal ultrafilter on I), it is shown that 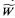 is a nonstandard model of X: i.e., the Transfer Principle holds for
is a nonstandard model of X: i.e., the Transfer Principle holds for 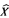 and
and 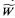 , if X is a flat set. Indeed, it is obvious that
, if X is a flat set. Indeed, it is obvious that 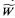 is not a nonstandard model of X when X is an infinite ordinal number. The construction of flat sets only requires the ZF axioms of set theory. Therefore, the assumption that X is a set of individuals (i.e., x ≠ ϕ and a ∈ x does not hold for x ∈ X and for any element a) is not needed for
is not a nonstandard model of X when X is an infinite ordinal number. The construction of flat sets only requires the ZF axioms of set theory. Therefore, the assumption that X is a set of individuals (i.e., x ≠ ϕ and a ∈ x does not hold for x ∈ X and for any element a) is not needed for 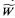 to be a nonstandard model of X.
to be a nonstandard model of X.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1994


