Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T13:34:24.902Z Has data issue: false hasContentIssue false
  • English
  • Français

Finitely approximable groups and actions Part II: Generic representations

Published online by Cambridge University Press:  12 March 2014

Christian Rosendal
Christian Rosendal*
Affiliation:
Department of Mathematics, Statistics, and Computer Science (M/C 249), University of Illinoisat Chicago, 851 S. Morgan St., Chicago, IL 60607-7045, USA, E-mail: [email protected], URL: http://www.math.uic.edu/~rosendal
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a finitely generated group Γ we study the space Isom(Γ, 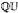) of all actions of Γ by isometries of the rational Urysohn metric space 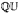, where Isom (Γ, 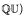) is equipped with the topology it inherits seen as a closed subset of Isom 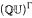. When Γ is the free group 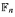on n generators this space is just Isom 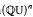, but is in general significantly more complicated. We prove that when Γ is finitely generated Abelian there is a generic point in Isom(Γ, 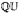), i.e., there is a comeagre set of mutually conjugate isometric actions of Γ on .

Keywords

Urysohn metric spacesubgroup separable groupsisometry groups
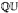Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 4 , December 2011 , pp. 1307 - 1321
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Akin, E., Hurley, M., and Kennedy, J. A., Dynamics of topologically generic homeomorphisms, Memoirs of the American Mathematical Society, vol. 164 (2003), no. 783.CrossRefGoogle Scholar
[2] Becker, H. and Kechris, A. S., The descriptive set theory of Polish group actions, London Mathematical Society Lecture Note Series, vol. 232, Cambridge University Press, 1996.CrossRefGoogle Scholar
[3] Bogopolski, O., Introduction to group theory, EMS Textbooks in Mathematics, European Mathematical Society, Zurich, 2008, translated, revised and expanded from the 2002 Russian original.CrossRefGoogle Scholar
[4] Coulbois, T., Free product, profinite topology and finitely generated subgroups, International Journal of Algebra and Computation, vol. 11 (2001), no. 2, pp. 171–184.CrossRefGoogle Scholar
[5] Glasner, E. and Weiss, B., Topological groups with Rokhlin properties, Colloquium Mathematicum, vol. 110 (2008), no. 1, pp. 51–80.CrossRefGoogle Scholar
[6] Jr.Hall, M., Coset representations in free groups, Transactions of the American Mathematical Society, vol. 67 (1949), no. 2, pp. 421–432.CrossRefGoogle Scholar
[7] Jr.Hall, M., A topology for free groups and related groups, Annals of Mathematics, Second Series, vol. 52 (1950), no. 1, pp. 127–139.CrossRefGoogle Scholar
[8] Herwig, B. and Lascar, D., Extending partial automorphisms and the profinite topology on free groups, Transactions of the American Mathematical Society, vol. 352 (2000), no. 5, pp. 1985–2021.CrossRefGoogle Scholar
[9] Hodges, W., Hodkinson, I., Lascar, D., and Shelah, S., The small index property for co-stable co-categorical structures and for the random graph, Journal of the London Mathematical Society, vol. 48 (1993), no. 2, pp. 204–218.CrossRefGoogle Scholar
[10] Ivanov, A. A., Generic expansions of ω-categorical structures and semantics of generalized quantifiers, this Journal, vol. 64 (1999), no. 2, pp. 775–789.Google Scholar
[11] Kechris, A. S., Classical descriptive set theory, Spinger Verlag, New York, 1995.CrossRefGoogle Scholar
[12] Kechris, A. S., Global aspects ofergodic group actions, Mathematical Surveys and Monographs, 160, American Mathematical Society, 2010.CrossRefGoogle Scholar
[13] Kechris, A. S. and Rosendal, C., Turbulence, amalgamation, and generic automorphisms of homogeneous structures, Proceedings of the London Mathematical Society, vol. 94 (2007), no. 2, pp. 302–350.CrossRefGoogle Scholar
[14] Lascar, D., Les beaux automorphismes, Archive for Mathematical Logic, vol. 31 (1991), no. 1, pp. 55–68.CrossRefGoogle Scholar
[15] Leiderman, A., Pestov, V., Rubin, M., Solecki, S., and Uspenskij, V., Special issue: Workshop on the Urysohn space Ben-Gurion University of the Negev, Beer Sheva, Israel 21–24 May 2006, Topology and its Applications, vol. 155 (2008), no. 14, pp. 1451–1634.CrossRefGoogle Scholar
[16] Macpherson, D. and Thomas, S., Comeagre conjugacy classes and free products with amalgamation, Discrete Mathematics, vol. 291 (2005), no. 1–3, pp. 135–142.CrossRefGoogle Scholar
[17] Mihaĭlova, K. A., The occurrence problem for direct products of groups, Rossiĭskaya Akademiya Nauk. Matematicheskiĭ Sbornik (N.S.), vol. 70 (1966), no. 112, pp. 241–251.Google Scholar
[18] Ribes, L. and Zalesskiĭ, P. A., On the profinite topology on a free group, The Bulletin of the London Mathematical Society, vol. 25 (1993), pp. 37–43.CrossRefGoogle Scholar
[19] Rosendal, C., The generic isometry and measure preserving homeomorphism are conjugate to their powers, Fundamenta Mathematicae, vol. 205 (2009), no. 1, pp. 1–27.CrossRefGoogle Scholar
[20] Rosendal, C., Finitely approximable groups and actions. Part I: The Ribes–Zalesskiĭ property, this Journal, vol. 76 (2011), no. 4, pp. 1297–1306.Google Scholar
[21] Solecki, S., Extending partial isometries, Israel Journal of Mathematics, vol. 150 (2005), pp. 315–332.CrossRefGoogle Scholar
[22] Truss, J. K., Generic automorphisms of homogeneous structures, Proceedings of the London Mathematical Society, vol. 65 (1992), no. 3, pp. 121–141.CrossRefGoogle Scholar
[23] Urysohn, P., Sur un espace métrique universel, Bulletin Sciences de Mathématiques, vol. 51 (1927), pp. 43–64, 74–90.Google Scholar
[24] Uspenskiĭ, V. V., On the group of isometries of the Urysohn universal metric space, Commentationes Mathematicae Universitatis Carolinae, vol. 31 (1990), no. 1, pp. 181–182.Google Scholar