Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T15:58:42.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Filtral powers of structures

Published online by Cambridge University Press:  12 March 2014

P. Ouwehand  and
H. Rose
P. Ouwehand
Affiliation:
Department of Mathematics and Applied Mathematics, University of Cape Town, Rondebosch 7700, South Africa. E-mail: [email protected]
H. Rose
Affiliation:
Department of Mathematics and Applied Mathematics, University of Cape Town, Rondebosch 7700, South Africa. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Among the results of this paper are the following:

1. Every Boolean (ultra)power is the union of an updirected elementary family of direct ultrapowers.

2. Under certain conditions, a finitely iterated Boolean ultrapower is isomorphic to a single Boolean ultrapower.

3. A ω-bounded filtral power is an elementary substructure of a filtral power.

4. Let 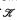be an elementary class closed under updirected unions (e.g., if 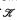is an amalgamation class); then 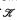is closed under finite products if and only if 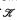is closed under reduced products if and only if 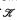is a Horn class.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 4 , December 1998 , pp. 1239 - 1254
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Ash, C. J., Reduced powers and Boolean extensions, Journal of the London Mathematical Society, vol. 9 (1975), pp. 429–432.Google Scholar
[2] Banaschewski, B. and Nelson, E., Elementary properties of limit reduced powers with applications to Boolean powers, Colloquia Mathematica Societatis János Bolyai, vol. ? (1975), pp. 21–24.Google Scholar
[3] Banaschewski, B. and Nelson, E., Boolean powers as algebras of continuous functions, Dissertationes Mathematica, no. 179, Warsaw, 1980.Google Scholar
[4] Bergman, C., The amalgamation class of a discriminator variety is finitely axiomatizable, Universal algebra and lattice theory, proceedings, puebla 1982, Lecture Notes in Mathematics, no. 1004, Springer-Verlag, 1983, pp. 1–9.Google Scholar
[5] Bergman, C., Amalgamation classes of some distributive varieties, Algebra Universalis, vol. 20 (1985), pp. 143–166.Google Scholar
[6] Bruyns, P., Naturman, C., and Rose, H., Amalgamation in the pentagon variety, Algebra Universalis, vol. 29 (1992), pp. 303–322.Google Scholar
[7] Burris, S., Boolean powers, Algebra Universalis, vol. 5 (1975), pp. 341–360.CrossRefGoogle Scholar
[8] Burris, S., Boolean constructions, Universal algebra and lattice theory, proceedings, puebla 1982, Lecture Notes in Mathematics, no. 1004, Springer-Verlag, 1983, pp. 67–90.Google Scholar
[9] Chang, C. C. and Keisler, H. J., Model theory, Studies in Logic and the Foundations of Mathematics, no. 73, North-Holland, Amsterdam-London, 1978.Google Scholar
[10] Hodges, W., Model theory, Encyclopedia of Mathematics and its Applications, no. 42, Cambridge University Press, 1993.CrossRefGoogle Scholar
[11] Jipsen, P. and Rose, H., Absolute retracts and amalgamation in certain congruence distributive varieties, Canadian Mathematics Bulletin, vol. 32 (1989), pp. 309–313.CrossRefGoogle Scholar
[12] Mansfield, R., The theory of Boolean ultrapowers, Annals of Mathematical Logic, vol. 2 (1971), pp. 297–325.Google Scholar
[13] Monk, J. D. and Bonnet, R. (editors), Handbook of Boolean algebras, vol. 1–3, North-Holland, Amsterdam-New York-Oxford-Tokyo, 1989.Google Scholar
[14] Taylor, W., Residually small varieties, Algebra Universalis, vol. 2 (1972), pp. 33–53.CrossRefGoogle Scholar
[15] Yasuhara, M., The amalgamation property, the universal-homogeneous models and generic models, Mathematica Scandinavica, vol. 34 (1973), pp. 5–36.Google Scholar