Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T22:28:09.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Existentially closed models of the theory of artinian local rings

Published online by Cambridge University Press:  12 March 2014

Hans Schoutens
Hans Schoutens*
Affiliation:
Mathematics Department, Wesleyan University, Middletown, CT 06459, US Fields Institute, 222 College Street, Toronto, Ontario, M5T 3J1, Canada E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The class of all Artinian local rings of length at most l is ∀2-elementary, axiomatised by a finite set of axioms 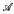τtl. We show that its existentially closed models are Gorenstein. of length exactly l and their residue fields are algebraically closed, and, conversely, every existentially closed model is of this form. The theory 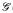oτl of all Artinian local Gorenstein rings of length l with algebraically closed residue field is model complete and the theory 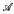τtl is companionable, with model-companion 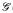oτl.

Keywords

model theoryexistentially closed modelsArtinian local ringsGorenstein rings
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 2 , June 1999 , pp. 825 - 845
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Bass] Bass, H., On the ubiquity of Gorenstein rings, Mathematische Zeitschrift, vol. 82 (1963), pp. 8–28.Google Scholar
[BH] Bruns, W. and Herzog, J., Cohen-Macaulay rings, Cambridge University Press, Cambridge, 1993.Google Scholar
[Coh] Cohen, I. S., On the structure and ideal theory of complete local rings, Transactions of the American Mathematical Society, vol. 59 (1946), pp. 54–106.CrossRefGoogle Scholar
[Hod1] Hodges, W., Building Models by Games, Cambridge University Press, Cambridge, 1985.Google Scholar
[Hod2] Hodges, W., Model Theory, Cambridge University Press, Cambridge, 1993.Google Scholar
[JL] Jensen, C. U. and Lenzing, H., Model Theoretic Algebra, Algebra, Logic and Applications Series, vol. 2, Gordon and Breach Science Publishers, Cambridge, 1989.Google Scholar
[Mats] Matsumura, H., Commutative ring theory, Cambridge University Press, Cambridge, 1986.Google Scholar
[Rob] Robinson, A., Introduction to model theory and to the metamathematics of algebra, North Holland, Amsterdam, 1965.Google Scholar
[Sch1] Schoutens, H., Rings which are generically Gorenstein, To appear, 1994.Google Scholar
[Sch3] Schoutens, H., The Primary Spectrum, To appear, 1995.Google Scholar
[Sch2] Schoutens, H., Existentially closed models of the theory of Artinian local rings, To appear in This Journal, 1999.Google Scholar