Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T18:48:20.201Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of some sparse sets of nonstandard natural numbers

Published online by Cambridge University Press:  12 March 2014

Renling Jin
Renling Jin*
Affiliation:
Department of Mathematics, College of Charleston, Charleston, SC 29424, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Answers are given to two questions concerning the existence of some sparse subsets of ℋ = {0, 1 … ., H – 1} ⊆ *ℕ. where H is a hyperfinite integer. In §1. we answer a question of Kanovei by showing that for a given cut U in ℋ, there exists a countably determined set X ⊆ ℋ which contains exactly one element in each U-monad, if and only if U = a · ℕ for some a Є ℋ ∖ {0}. In §2, we deal with a question of Keisler and Leth in [6]. We show that there is a cut V ⊆ ℋ such that for any cut U, (i) there exists a U-discrete set X ⊆ ℋ with X + X = ℋ (mod H) provided 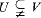, (ii) there does not exist any U-discrete set X ⊆ ℋ with X + X = ℋ (mod H) provided 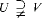. We obtain some partial results for the case U = V.

Keywords

hyperfinite integercutcountably determined setU-discrete set
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 2 , June 2001 , pp. 959 - 973
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chang, C. C. and Keisler, H. J., Model Theory, third ed., North-Holland, 1990.Google Scholar
[2]Henson, C. W., Analytic sets, Baire sets and the standard part map, Canadian Journal of Mathematics, vol. 31 (1979), pp. 663–672.CrossRefGoogle Scholar
[3]Henson, C. W., Foundations of nonstandard analysis: a gentle introduction to nonstandard extensions, Nonstandard analysis: Theory and applications (Cutland, N. J., Henson, C. W., and Arkeryd, L., editors), Kluwer Publishers, Dordrecht, 1997, pp. 1–49.Google Scholar
[4]Henson, C. W. and Ross, D., Analytic mappings on hyperfinite sets, Proceedings of the American Mathematical Society, vol. 118 (1993), pp. 587–596.CrossRefGoogle Scholar
[5]Keisler, H. J., Kunen, K., Leth, S. C., and Miller, A. W., Descriptive set theory over hyperfinite sets, this Journal, vol. 54 (1989), pp. 1167–1180.Google Scholar
[6]Keisler, H. J. and Leth, S. C., Meager sets on the hyperfinite timeline, this Journal, vol. 56 (1991), pp. 71–102.Google Scholar
[7]Lindstrøm, T., An invitation to nonstandard analysis, Nonstandard analysis and its applications (Cutland, N., editor), Cambridge University Press, Cambridge, 1988, pp. 1–105.Google Scholar
[8]Živaljević, B., U-meager sets when the cofinality and the coinitiality of U are uncountable, this Journal, vol. 56 (1991), pp. 906–914.Google Scholar