THE EXACT STRENGTH OF THE CLASS FORCING THEOREM

Abstract

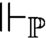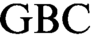The class forcing theorem, which asserts that every class forcing notion ${\mathbb {P}}$ admits a forcing relation $\Vdash _{\mathbb {P}}$ , that is, a relation satisfying the forcing relation recursion—it follows that statements true in the corresponding forcing extensions are forced and forced statements are true—is equivalent over Gödel–Bernays set theory $\text {GBC}$ to the principle of elementary transfinite recursion 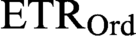$\text {ETR}_{\text {Ord}}$ for class recursions of length 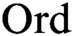$\text {Ord}$ . 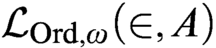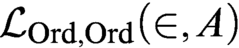It is also equivalent to the existence of truth predicates for the infinitary languages $\mathcal {L}_{\text {Ord},\omega }(\in ,A)$ , allowing any class parameter A; to the existence of truth predicates for the language $\mathcal {L}_{\text {Ord},\text {Ord}}(\in ,A)$ ; to the existence of $\text {Ord}$ -iterated truth predicates for first-order set theory 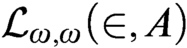$\mathcal {L}_{\omega ,\omega }(\in ,A)$ ; to the assertion that every separative class partial order 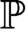${\mathbb {P}}$ has a set-complete class Boolean completion; to a class-join separation principle; and to the principle of determinacy for clopen class games of rank at most 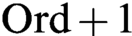$\text {Ord}+1$ . 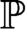Unlike set forcing, if every class forcing notion ${\mathbb {P}}$ has a forcing relation merely for atomic formulas, then every such ${\mathbb {P}}$ has a uniform forcing relation applicable simultaneously to all formulas. Our results situate the class forcing theorem in the rich hierarchy of theories between 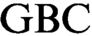$\text {GBC}$ and Kelley–Morse set theory 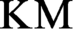$\text {KM}$ .