Article contents
Every n-generic degree is a minimal cover of an n-generic degree
Published online by Cambridge University Press: 12 March 2014
Extract
The notions of forcing and generic set were introduced by Cohen in 1963 to prove the independence of the Axiom of Choice and the Continuum Hypothesis in set theory. Let ω be the set of natural numbers, i.e., {0,1,2,3,…}. A string is a mapping from an initial segment of ω into {0,1}. We identify a set A ⊆ ω to with its characteristic function.
We now consider a set generic over the arithmetic sets. A set A ⊆ ω is called n-generic if it is Cohen-generic for n-quantifier arithmetic. This is equivalent to saying that for every 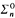 -set of strings S, there is a σ ⊂ A such that σ ∈ S or (∀v ≥ σ)(v ∉ S). By degree we mean Turing degree (of unsolvability). We call a degree n-generic if it has an n-generic representative. For a degree a, let D(≤a) denote the set of degrees which are recursive in a.
-set of strings S, there is a σ ⊂ A such that σ ∈ S or (∀v ≥ σ)(v ∉ S). By degree we mean Turing degree (of unsolvability). We call a degree n-generic if it has an n-generic representative. For a degree a, let D(≤a) denote the set of degrees which are recursive in a.
Before Cohen's work, there was a precursor of the notion of forcing in recursion theory. Friedberg showed that for every degree b above the complete degree 0', i.e., the degree of a complete r.e. set, there is a degree a such that a′ = a ⋃ 0′ = b. He actually proved this result by using the notion of forcing for 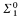 statements.
statements.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993
References
REFERENCES
- 3
- Cited by


