Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-14T11:17:12.899Z Has data issue: false hasContentIssue false
  • English
  • Français

Effective presentability of Boolean algebras of Cantor-Bendixson rank 1

Published online by Cambridge University Press:  12 March 2014

Rod Downey  and
Carl G. Jockusch Jr.
Rod Downey
Affiliation:
Department of Mathematics, Victoria University of Wellington, Department of Mathematics, Wellington, New Zealand E-mail: [email protected]
Carl G. Jockusch Jr.
Affiliation:
Department of Mathematics, University of Illinois, 1409 West Green Street, Urbana, Il 61801–2917, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that there is a computable Boolean algebra 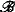and a computably enumerable ideal I of 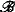such that the quotient algebra 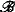/I is of Cantor-Bendixson rank 1 and is not isomorphic to any computable Boolean algebra. This extends a result of L. Feiner and is deduced from Feiner's result even though Feiner's construction yields a Boolean algebra of infinite Cantor-Bendixson rank.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 1 , March 1999 , pp. 45 - 52
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Downey, R., On presentations of algebraic structures, Complexity, logic and recursion theory (Sorbi, A., editor), Lecture Notes in Pure and Applied Mathematics, vol. 197, Marcel Dekker, 1997, pp. 157–206.Google Scholar
[2]Downey, R. and Jockusch, C., Every low Boolean algebra is isomorphic to a recursive one, Proceedings of the American Mathematical Society, vol. 122 (1994), pp. 871–880.CrossRefGoogle Scholar
[3]Feiner, L., Hierarchies of Boolean algebras, this Journal, vol. 35 (1970), pp. 365–374.Google Scholar
[4]Feiner, L., Degrees of nonrecursive presentability, Proceedings of the American Mathematical Society, vol. 38 (1973), pp. 621–624.CrossRefGoogle Scholar
[5]Jockusch, C. and Soare, R., Boolean algebras, Stone spaces, and the iterated Turing jump, this Journal, vol. 59 (1994), pp. 1121–1138.Google Scholar
[6]Ketonen, J., The structure of countable Boolean algebras, Annals of Mathematics, vol. 108 (1978), pp. 41–89.CrossRefGoogle Scholar
[7]Koppelberg, Sabine, General theory of Boolean algebras, Handbook of Boolean algebras (Monk, J. D. and Bonnet, R., editors), vol. 1, North-Holland, Amsterdam, New York, Oxford, Tokyo, 1989.Google Scholar
[8]Pierce, R. S., Countable Boolean algebras, Handbook of Boolean algebras (Monk, J. D. and Bonnet, R., editors), vol. 3, North-Holland, Amsterdam, New York, Oxford, Tokyo, 1989, pp. 775–876.Google Scholar
[9]Remmel, J., Recursive Boolean algebras, Handbook of Boolean algebras (Monk, J. D. and Bonnet, R., editors), vol. 3, North-Holland, Amsterdam, New York, Oxford, Tokyo, 1989, pp. 1097–1166.Google Scholar
[10]Soare, R. I., Recursively enumerable sets and degrees; A study of computable functions and computably generated sets, Springer-Verlag, Heidelberg, 1987.Google Scholar
[11]Soare, R. I., Computability and recursion, Bulletin of Symbolic Logic, vol. 2 (1996), pp. 284–321.CrossRefGoogle Scholar
[12]Thurber, J., Recursive and r.e. quotient Boolean algebras, Archive for Mathematical Logic, vol. 33 (1994), pp. 121–129.CrossRefGoogle Scholar
[13]Thurber, J., Every low2 Boolean algebra has a recursive copy, Proceedings of the American Mathematical Society, vol. 123 (1995), pp. 3859–3966.Google Scholar