Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T20:22:59.151Z Has data issue: false hasContentIssue false
  • English
  • Français

DOWNWARD TRANSFERENCE OF MICE AND UNIVERSALITY OF LOCAL CORE MODELS

Published online by Cambridge University Press:  19 June 2017

ANDRÉS EDUARDO CAICEDO  and
MARTIN ZEMAN
ANDRÉS EDUARDO CAICEDO
Affiliation:
DEPARTMENT OF MATHEMATICS BOISE STATE UNIVERSITY 1910 UNIVERSITY DRIVE BOISE, ID83725, USA E-mail: [email protected]: http://math.boisestate.edu/∼caicedo
MARTIN ZEMAN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA AT IRVINE IRVINE, CA92697, USA E-mail: [email protected]: http://www.math.uci.edu/∼mzeman/
Get access Rights & Permissions [Opens in a new window]

Abstract

If M is a proper class inner model of ZFC and 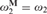$\omega _2^{\bf{M}} = \omega _2 $, then every sound mouse projecting to ω and not past 0 belongs to M. In fact, under the assumption that 0 does not belong to M, 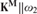${\bf{K}}^{\bf{M}} \parallel \omega _2 $ is universal for all countable mice in V.

Similarly, if M is a proper class inner model of ZFC, δ > ω1 is regular, (δ+)M = δ+ and in V there is no proper class inner model with a Woodin cardinal, then 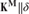${\bf{K}}^{\bf{M}} \parallel \delta $ is universal for all mice in V of cardinality less than δ.

Keywords

Primary 03E45Secondary 03E0503E55core modeluniversalityWoodin cardinalΣ31-correctness
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 385 - 419
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abraham, U., On forcing without the continuum hypothesis, this Journal, vol. 48 (1983), no. 3, pp. 658–661.Google Scholar
Caicedo, A. E., Cardinal preserving elementary embeddings , Logic Colloquium 2007 (Delon, F., Kohlenbach, U., Maddy, P., and Stephan, F., editors), Lecture Notes in Logic, vol. 35, Association for Symbolic Logic, La Jolla, CA, 2010, pp. 14–31.CrossRefGoogle Scholar
Caicedo, A. E. and Veličković, B., The bounded proper forcing axiom and well orderings of the reals . Mathematical Research Letters, vol. 13 (2006), no. 2–3, pp. 393–408.Google Scholar
Claverie, B. and Schindler, R. D., Woodin’s axiom (*), bounded forcing axioms, and precipitous ideals on ω 1 , this Journal, vol. 77 (2012), no. 2, pp. 475–498.Google Scholar
Cox, S., Covering theorems for the core model, and an application to stationary set reflection . Annals of Pure and Applied Logic, vol. 161 (2009), no. 1, pp. 66–93.CrossRefGoogle Scholar
Foreman, M. D. and Magidor, M., Large cardinals and definable couterexamples to the continuum hypothesis . Annals of Pure and Applied Logic, vol. 76 (1995), no. 1, pp. 47–97.CrossRefGoogle Scholar
Friedman, S. D., $0^\sharp $ and inner models, this Journal, vol. 67 (2002), no. 3, pp. 924–932.Google Scholar
Friedman, S. D., BPFA and inner models . Annals of the Japan Association for Philosophy of Science (Special Issue on Mathematical Logic and its Applications), vol. 19 (2011), pp. 29–36.Google Scholar
Hjorth, G., The size of the ordinal u 2 . Journal of the London Mathematical Society, Second Series, vol. 52 (1995), no. 3, pp. 417–433.Google Scholar
Jensen, R. B., On some problems of Mitchell, Welch and Vickers, unpublished manuscript, 1990. Available (under L-forcing) at www.mathematik.hu-berlin.de/∼raesch/org/jensen.html.Google Scholar
Jensen, R. B., Addendum to “A new fine structure for higher core models”, unpublished manuscript, 1998. Available at http://www.mathematik.hu-berlin.de/∼raesch/org/jensen.html.Google Scholar
Jensen, R. B. and Steel, J. R., K without the measurable, this Journal, vol. 78 (2013), no. 3, pp. 708–734.Google Scholar
Mitchell, W. J. and Schimmerling, E., Covering without countable closure . Mathematical Research Letters, vol. 2 (1995), no. 5, pp. 595–609.Google Scholar
Mitchell, W. J. and Schindler, R. D., A universal extender model without large cardinals in V, this Journal, vol. 69 (2004), no. 2, pp. 371–386.Google Scholar
Mitchell, W. J. and Steel, J. R., Fine Structure and Iteration Trees, Lecture Notes in Logic, vol. 3, Springer, Berlin, 1994.Google Scholar
Neeman, I., Forcing with sequences of models of two types . Notre Dame Journal of Formal Logic, vol. 55 (2014), no. 2, pp. 265–298.CrossRefGoogle Scholar
Räsch, T. and Schindler, R. D., A new condensation principle . Archive for Mathematical Logic, vol. 44 (2005), no. 2, pp. 159–166.CrossRefGoogle Scholar
Schimmerling, E. and Steel, J. R., The maximality of the core model . Transactions of American Mathematical Society, vol. 351 (1999), no. 8, pp. 3119–3141.Google Scholar
Schindler, R. D., A simple proof of ${\rm{\Sigma }}_3^1 $ -correctness of K, unpublished manuscript, 2001. Available at http://www.math.uni-muenster.de/logik/Personen/rds/.Google Scholar
Schindler, R. D., Sharps and the ${\rm{\Sigma }}_3^1 $ -correctness of K, unpublished manuscript, 2001. Available at http://www.math.uni-muenster.de/logik/Personen/rds/.Google Scholar
Steel, J. R., The Core Model Iterability Problem , Lecture Notes in Logic, vol. 8, Springer, Berlin, 1996.Google Scholar
Steel, J. R., PFA implies $AD^{{\bf{L}}\left( \right)} $ , this Journal, vol. 70 (2005), no. 4, pp. 1255–1296.Google Scholar
Steel, J. R., An outline of Inner Model Theory , Handbook of Set Theory, vol. 3 (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 1595–1684.Google Scholar
Steel, J. R. and Welch, P. D., ${\rm{\Sigma }}_3^1 $ -absoluteness and the second uniform indiscernible . Israel Journal of Mathematics, vol. 104 (1998), pp. 157–190.Google Scholar
Todorčević, S., Conjectures of Rado and Chang and cardinal arithmetic , Finite and Infinite Combinatorics in Sets and Logic (Banff, AB, 1991) (Sauer, N. W., Woodrow, R. E., and Sands, B., editors), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 411, Kluwer Academic Publishers, Dordrecht, 1993, pp. 385–398.Google Scholar
Veličković, B., Forcing axioms and stationary sets . Advances in Mathematics, vol. 94 (1992), no. 2, pp. 256–284.Google Scholar
Welch, P. D., Σ*-fine structure theory , Handbook of Set Theory, vol. 1 (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 657–736.Google Scholar
Zeman, M., Inner Models and Large Cardinals, DeGruyter Series in Logic and its Applications, vol. 5, DeGruyter, Berlin, 2002.CrossRefGoogle Scholar