Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T18:32:00.753Z Has data issue: false hasContentIssue false
  • English
  • Français

Domination, forcing, array nonrecursiveness and relative recursive enumerability

Published online by Cambridge University Press:  12 March 2014

Mingzhong Cai  and
Richard A. Shore
Mingzhong Cai
Affiliation:
Department of Mathematics, Cornell University, Ithaca NY 14853, USA, E-mail: [email protected]
Richard A. Shore
Affiliation:
Department of Mathematics, Cornell University, Ithaca NY 14853, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present some abstract theorems showing how domination properties equivalent to being 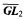or array nonrecursive can be used to construct sets generic for different notions of forcing. These theorems are then applied to give simple proofs of some known results. We also give a direct uniform proof of a recent result of Ambos-Spies, Ding, Wang, and Yu [2009] that every degree above any in 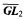is recursively enumerable in a 1-generic degree strictly below it. Our major new result is that every array nonrecursive degree is r.e. in some degree strictly below it. Our analysis of array nonrecursiveness and construction of generic sequences below ANR degrees also reveal a new level of uniformity in these types of results.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 1 , March 2012 , pp. 33 - 48
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ambos-Spies, K., Ding, D., Wang, W., and Yu, L. [2009], Bounding non-GL2 and R.E.A, this Journal, vol. 74, no. 3, pp. 989–1000.Google Scholar
Cai, M. [2010], A 2-minimal non-GL2 degree, Journal of Mathematical Logic, vol. 10, no. 1–2, pp. 1–30.CrossRefGoogle Scholar
Cai, M. [2012], Array nonrecursiveness and relative recursive enumerability, this Journal, vol. 77, pp. 21–32.Google Scholar
Downey, R., Jockusch, C., and Stob, M. [1990], Array nonrecursive sets and multiple permitting arguments, Recursion theory week (Ambos-Spies, K., Müller, G. H., and Sacks, G. E., editors), Springer-Verlag, Berlin, pp. 141–174.CrossRefGoogle Scholar
Harizanov, V. [1998], Turing degrees of certain isomorphic images of computable relations, Annals of Pure and Applied Logic, vol. 93, pp. 103–113.CrossRefGoogle Scholar
Hirschfeldt, D. and Shore, R. A. [2007], Combinatorial principles weaker than Ramsey's theorem for pairs, this Journal, vol. 72, pp. 171–206.Google Scholar
Jockusch, C. G. Jr. and Posner, D. B. [1978], Double jumps of minimal degrees, this Journal, vol. 43, pp. 715–724.Google Scholar
Lerman, M. [1983], Degrees of unsolvability, Perspectives in Mathematical Logic, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Robinson, R. W. [1971], Jump restricted interpolation in the recursively enumerable degrees, Annals of Mathematics. Second Series, vol. 93, pp. 586–596.CrossRefGoogle Scholar
Shoenfield, J. R. [1959], On degrees of unsolvability, Annals of Mathematics. Second Series, vol. 69, pp. 644–653.CrossRefGoogle Scholar
Shore, R. A. [1981], The theory of the degrees below O', The Journal of the London Mathematical Society. Second Series, vol. 24, pp. 1–14.CrossRefGoogle Scholar
Shore, R. A. [2007], Direct and local definitions of the Turing jump, Journal of Mathematical Logic, vol. 7, pp. 229–262.CrossRefGoogle Scholar
Wang, W. [2011], Relative enumerability and 1-genericity, this Journal, vol. 76, pp. 897–913.Google Scholar
Yu, L. [2006], Lowness for genericity, Archive for Mathematical Logic, vol. 45, pp. 233–238.CrossRefGoogle Scholar