Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-05T02:14:39.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Distributivity and an axiom of choice

Published online by Cambridge University Press:  12 March 2014

George E. Collins
George E. Collins*
Affiliation:
The State University of Iowa, Iowa City, Iowa Cornell University, Ithaca, N.Y.
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper a theorem will be established which states that a particular axiom of choice is equivalent to complete distributivity of union and intersection. The theorem will be formulated and proved in the system of logic of [4]. In addition to definitions of [4], the following will be used.

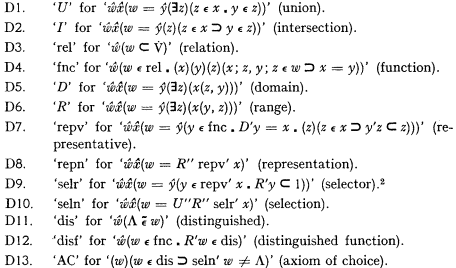
In terms of these definitions, the theorem can be formulated as follows.

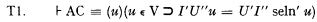
The dual of this statement, obtained by interchanging I and U, is also a theorem and has a similar proof.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 19 , Issue 4 , December 1954 , pp. 275 - 277
Copyright
Copyright © Association for Symbolic Logic 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Birkhoff, Garrett, Lattice theory, American Mathematical Society Colloquium Publications, vol. 25, revised edition, 1948, pp. 146–147.Google Scholar
[2]Hahn, Hans, Reele Funktionen, Erster Teil, Leipzig, 1932, p. 10.Google Scholar
[3]Hausdorff, F., Mengenlehre, Dritte Auflage, 1935, p. 19.Google Scholar
[4]Quine, W. V., Mathematical logic, revised edition. Harvard, 1951.CrossRefGoogle Scholar
[5]Vaidyanathaswamy, R., Treatise on set topology, Part I, 1947, p. 3.Google Scholar