Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T12:03:12.642Z Has data issue: false hasContentIssue false
  • English
  • Français

DISCRETE METRIC SPACES: STRUCTURE, ENUMERATION, AND 0-1 LAWS

Published online by Cambridge University Press:  19 August 2019

DHRUV MUBAYI  and
CAROLINE TERRY
DHRUV MUBAYI
Affiliation:
DEPARTMENT OF MATHEMATICS, STATISTICS, AND COMPUTER SCIENCE UNIVERSITY OF ILLINOIS AT CHICAGO 851 S MORGAN STREET CHICAGO, IL60607, USA E-mail: [email protected]
CAROLINE TERRY
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CHICAGO 5734 S UNIVERSITY AVENUE CHICAGO, IL60637, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fix an integer 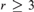$r \ge 3$. We consider metric spaces on n points such that the distance between any two points lies in 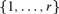$\left\{ {1, \ldots ,r} \right\}$. Our main result describes their approximate structure for large n. As a consequence, we show that the number of these metric spaces is 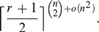$\left\lceil {{{r + 1} \over 2}} \right\rceil ^{\left( {\matrix{ n \cr 2 \cr } } \right) + o\left( {n^2 } \right)} .$

Related results in the continuous setting have recently been proved by Kozma, Meyerovitch, Peled, and Samotij [34]. When r is even, our structural characterization is more precise and implies that almost all such metric spaces have all distances at least 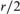$r/2$. As an easy consequence, when r is even, we improve the error term above from 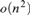$o\left( {n^2 } \right)$ to 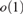$o\left( 1 \right)$, and also show a labeled first-order 0-1 law in the language 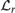${\cal L}_r $, consisting of r binary relations, one for each element of 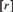$[r]$ . In particular, we show the almost sure theory T is the theory of the Fraïssé limit of the class of all finite simple complete edge-colored graphs with edge colors in 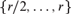$\left\{ {r/2, \ldots ,r} \right\}$.

Our work can be viewed as an extension of a long line of research in extremal combinatorics to the colored setting, as well as an addition to the collection of known structures that admit logical 0-1 laws.

Keywords

03C1305A160-1 lawsasymptotic enumerationdiscrete metric spaces
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 4 , December 2019 , pp. 1293 - 1325
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlman, O. and Koponen, V., Random l-colourable structures with a pregeometry. Mathematical Logic Quarterly, vol. 63 (2017), no. 1–2, pp. 32–58.CrossRefGoogle Scholar
Axenovich, M. and Martin, R., A version of szemerédi’s regularity lemma for multicolored graphs and directed graphs that is suitable for induced graphs, 2011, arXiv:1106.2871v1 [math.CO].Google Scholar
Balogh, J., Bollobás, B., and Simonovits, M., The number of graphs without forbidden subgraphs. Journal of Combinatorial Theory, Series B, vol. 91 (2004), no. 1, pp. 1–24.CrossRefGoogle Scholar
Balogh, J., Bollobás, B., and Simonovits, M., The typical structure of graphs without given excluded subgraphs. Random Structures Algorithms, vol. 34 (2009), no. 3, pp. 305–318.CrossRefGoogle Scholar
Balogh, J., Bollobás, B., and Simonovits, M., The fine structure of octahedron-free graphs. Journal of Combinatorial Theory, Series B, vol. 101 (2011), no. 2, pp. 67–84.CrossRefGoogle Scholar
Balogh, J. and Mubayi, D., Almost all triple systems with independent neighborhoods are semi-bipartite. Journal of Combinatorial Theory, Series A, vol. 118 (2011), no. 4, pp. 1494–1518.CrossRefGoogle Scholar
Balogh, J. and Mubayi, D., Almost all triangle-free triple systems are tripartite. Combinatorica, vol. 32 (2012), no. 2, pp. 143–169.CrossRefGoogle Scholar
Balogh, J. and Samotij, W., The number of $$K_{s,t} $-free graphs. Journal of the London Mathematical Society (2) ), vol. 83 (2011), no. 2, pp. 368–388.CrossRefGoogle Scholar
Bell, J. P., Sufficient conditions for zero-one laws. Transactions of the American Mathematical Society, vol. 354 (2002), no. 2, pp. 613–630 (electronic).CrossRefGoogle Scholar
Bollobás, B., Random Graphs, second ed., Cambridge Studies in Advanced Mathematics, vol. 73, Cambridge University Press, Cambridge, 2001.CrossRefGoogle Scholar
Brightwell, G. and Goodall, S., The number of partial orders of fixed width. Order, vol. 13 (1996), no. 4, pp. 315–337.CrossRefGoogle Scholar
Brightwell, G., Grable, D. A., and Prömel, H. J., Forbidden induced partial orders. Discrete Mathematics, vol. 201 (1999), no. 1–3, pp. 53–80.CrossRefGoogle Scholar
Burris, S. and Yeats, K., Sufficient conditions for labelled 0-1 laws. Discrete Mathematics and Theoretical Computer Science, vol. 10 (2008), no. 1, pp. 147–156.Google Scholar
Chabukswar, R. and Tievsky, A., Almost monochromatic triangles and other ramsey problem variants, preprint, 2004, http://users.ece.cmu.edu/∼rchabuks/main.pdf.Google Scholar
Compton, K. J., A logical approach to asymptotic combinatorics. I. First-order properties. Advances in Mathematics, vol. 65 (1987), no. 1, pp. 65–96.CrossRefGoogle Scholar
Compton, K. J., A logical approach to asymptotic combinatorics. II. Monadic second-order properties. Journal of Combinatorial Theory, Series A, vol. 50 (1989), no. 1, pp. 110–131.CrossRefGoogle Scholar
Conant, G. and Terry, C., Model theoretic properties of the Urysohn sphere. Annals of Pure and Applied Logic, vol. 167 (2016), no. 1, pp. 49–72.CrossRefGoogle Scholar
Delhommé, C., Laflamme, C., Pouzet, M., and Sauer, N., Divisibility of countable metric spaces. European Journal of Combinatorics, vol. 28 (2007), no. 6, pp. 1746–1769.CrossRefGoogle Scholar
Erdős, P., Frankl, P., and Rödl, V., The asymptotic number of graphs not containing a fixed subgraph and a problem for hypergraphs having no exponent. Graphs and Combinatorics, vol. 2 (1986), no. 2, pp. 113–121.CrossRefGoogle Scholar
Erdős, P., Kleitman, D. J., and Rothschild, B. L., Asymptotic enumeration of $r$K_n $-free graphs, Colloquio Internazionale sulle Teorie Combinatorie (Rome, 1973), Tomo II, Atti dei Convegni Lincei, vol. 17, Accad. Naz. Lincei, Rome, 1976, pp. 19–27.Google Scholar
Fagin, R., Probabilities on finite models, this Journal, vol. 41 (1976), no. 1, pp. 50–58.Google Scholar
Flum, J. and Grohe, M., Parameterized Complexity Theory, Texts in Theoretical Computer Science, Springer-Verlag, Berlin, 2006.Google Scholar
Füredi, Z. and Kündgen, A., Turán problems for integer-weighted graphs. Journal of Graph Theory, vol. 40 (2002), no. 4, pp. 195–225.CrossRefGoogle Scholar
Glebskiĭ, J. V., Kogan, D. I., Liogon’kiĭ, M. I., and Talanov, V. A., Volume and fraction of satisfiability of formulas of the lower predicate calculus. Otdelenie Matematiki, Mekhaniki i Kibernetiki Akademii Nauk Ukrainskoǐ SSR. Kibernetika (1969), no. 2, pp. 17–27.Google Scholar
Haber, S. and Krivelevich, M., The logic of random regular graphs. Journal of Combinatorics, vol. 1 (2010), no. 3–4, pp. 389–440.CrossRefGoogle Scholar
Heinig, P., Müller, T., Noy, M., and Taraz, A., Logical limit laws for minor-closed classes of graphs. Journal of Combinatorial Theory Series B, vol. 130 (2018), pp. 158–206.CrossRefGoogle Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Hundack, C., Prömel, H. J., and Steger, A., Extremal graph problems for graphs with a color-critical vertex. Combinatorics Probability and Computing, vol. 2 (1993), no. 4, pp. 465–477.CrossRefGoogle Scholar
Kleitman, D. J. and Rothschild, B. L., Asymptotic enumeration of partial orders on a finite set. Transactions of the American Mathematical Society, vol. 205 (1975), pp. 205–220.CrossRefGoogle Scholar
Kolaitis, P. G., Prömel, H. J., and Rothschild, B. L., $r $K_{l + 1} $-free graphs:Asymptotic structure and a 0–1 law. Transactions of the American Mathematical Society, vol. 303 (1987), no. 2, pp. 637–671.Google Scholar
Koponen, V., Asymptotic probabilities of extension properties and random l-colourable structures. Annals of Pure and Applied Logic, vol. 163 (2012), no. 4, pp. 391–438.CrossRefGoogle Scholar
Koponen, V., Random graphs with bounded maximum degree: Asymptotic structure and a logical limit law. Discrete Mathematics and Theoretical Computer Science, vol. 14 (2012), no. 2, pp. 229–254.Google Scholar
Koponen, V., A limit law of almost l-partite graphs, this Journal, vol. 78 (2013), no. 3, pp. 911–936.Google Scholar
Kozma, G., Meyerovitch, T., Peled, R., and Samotij, W., Random Points in the Metric Polytope, Slides of a Talk Given at Random Combinatorial Structures and Statistical Mechanics, May 6–10, Venice, Italy, 2013.Google Scholar
Kühn, D., Osthus, D., Townsend, T., and Zhao, Y., On the structure of oriented graphs and digraphs with forbidden tournaments or cycles. Journal of Combinatorial Theory, Series B, vol. 124 (2017), no. Supplement C, pp. 88–127.CrossRefGoogle Scholar
Lamken, E. and Rothschild, B. L., The numbers of odd-cycle-free graphs, Finite and Infinite Sets, Vols. I, II (Eger, 1981), Colloquia Mathematica Societatis János Bolyai, vol. 37, North-Holland, Amsterdam, 1984, pp. 547–553.Google Scholar
Lynch, J. F., Convergence law for random graphs with specified degree sequence. ACM Transactions on Computational Logic, vol. 6 (2005), no. 4, pp. 727–748.CrossRefGoogle Scholar
Malliaris, M. and Shelah, S., Regularity lemmas for stable graphs. Transactions of the American Mathematical Society, vol. 366 (2014), no. 3, pp. 1551–1585.CrossRefGoogle Scholar
Marker, D., Model Theory, Graduate Texts in Mathematics, vol. 217, Springer-Verlag, New York, 2002, An introduction.Google Scholar
Mascioni, V., Equilateral triangles in finite metric spaces. Electronic Journal of Combinatorics, vol. 11 (2004), no. 1, Research Paper 18, 20 pp. (electronic).Google Scholar
Mascioni, V., On the probability that finite spaces with random distances are metric spaces. Discrete Mathematics, vol. 300 (2005), no. 1–3, pp. 129–138.CrossRefGoogle Scholar
Mubayi, D. and Terry, C., Discrete metric spaces: Structure, enumeration, and 0-1 laws, this Journal, accepted, 2015, arXiv:1502.01212 [math.CO].Google Scholar
Person, Y. and Schacht, M., Almost all hypergraphs without Fano planes are bipartite, Proceedings of the Twentieth Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, Philadelphia, PA, 2009, pp. 217–226.CrossRefGoogle Scholar
Prömel, H. J. and Steger, A., The asymptotic number of graphs not containing a fixed color-critical subgraph. Combinatorica, vol. 12 (1992), no. 4, pp. 463–473.CrossRefGoogle Scholar
Robinson, R. W., Counting labeled acyclic digraphs, New directions in the theory of graphs (Proc. Third Ann Arbor Conf., Univ. Michigan, Ann Arbor, Mich., 1971 ), Academic Press, New York, 1973, pp. 239–273.Google Scholar
Shelah, S., Toward classifying unstable theories. Annals of Pure and Applied Logic, vol. 80 (1996), no. 3, pp. 229–255.CrossRefGoogle Scholar
Stanley, R. P., Acyclic orientations of graphs. Discrete Mathematics, vol. 5 (1973), pp. 171–178.CrossRefGoogle Scholar
Tent, K. and Ziegler, M., A Course in Model Theory, Lecture Notes in Logic, vol. 40, Association for Symbolic Logic, La Jolla, CA; Cambridge University Press, Cambridge, 2012.CrossRefGoogle Scholar
Winkler, P., Random structures and zero-one laws, Finite and Infinite Combinatorics in Sets and Logic (Banff, AB, 1991), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, vol. 411, Kluwer Academic Publishers, Dordrecht, 1993, pp. 399–420.CrossRefGoogle Scholar