Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T23:38:57.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Diophantine properties of sets definable in o-minimal structures

Published online by Cambridge University Press:  12 March 2014

A. J. Wilkie
A. J. Wilkie*
Affiliation:
Mathematical Institute, 24-29 ST Giles, Oxford OX1 3LB, UK, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Let 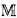be an o-minimal expansion of the ordered field of real numbers 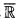, and let S be an 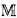-definable subset (parameters allowed unless otherwise stated) of ℝn. In this note I investigate questions concerning the distribution of points on S with integer coordinates. My main theorem gives an estimate which, though probably far from best possible, at least shows that the o-minimal assumption does have diophantine consequences. This is, perhaps, surprising in view of the flexibility that we now seem to have in constructing o-minimal expansions of 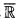(see, e. g. [7], [8], [9]).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 3 , September 2004 , pp. 851 - 861
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baker, A., Transcendental number theory, CUP, 1975.CrossRefGoogle Scholar
[2]Denef, J. and van den Dries, L., p-adic and real subanalytic sets, Annals of Mathematics, vol. 128 (1988), pp. 79–138.CrossRefGoogle Scholar
[3]van den Dries, L., A generalization of the Tarski-Seidenberg theorem, and some nondefinability results, Bulletin of AMS, vol. 15 (1986), pp. 189–193.CrossRefGoogle Scholar
[4]van den Dries, L., Tame topology and o-minimal structures, LMS Lecture Note Series, vol. 248, CUP, 1998.CrossRefGoogle Scholar
[5]Halberstam, H., Transcendental numbers, The Mathematical Gazette, (1974), pp. 276–284.Google Scholar
[6]Nesterenko, Y. V. and Philippon, P. (editors), Introduction to algebraic independence theory, Lecture Notes in Mathematics, vol. 1752, Springer, 2001.CrossRefGoogle Scholar
[7]Rolin, J.-P., Speissegoer, P., and Wilkie, A. J., Quasianalytic Denjoy-Carleman classes and o-minimality, Journal of the American Mathematical Society, vol. 16 (2003), no. 4, pp. 751–777.CrossRefGoogle Scholar
[8]Speissegger, P., The Pfaffian closure of an o-minimal structure, Journal für die Reineund Angewandte Mathematik, vol. 508 (1999), pp. 189–211.CrossRefGoogle Scholar
[9]Wilkie, A. J., A theorem of the complement and some new o-minimal structures, Selecta Mathematica. New Series, vol. 5 (1999), pp. 397–421.CrossRefGoogle Scholar