Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T10:19:04.096Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DETERMINED PROPERTY OF BAIRE IN REVERSE MATH

Published online by Cambridge University Press:  10 September 2019

ERIC P. ASTOR ,
DAMIR DZHAFAROV ,
ANTONIO MONTALBÁN ,
REED SOLOMON  and
LINDA BROWN WESTRICK
ERIC P. ASTOR
Affiliation:
GOOGLE LLC, 111 8TH AVE. NEW YORK, NY10011, USAE-mail:[email protected]
DAMIR DZHAFAROV
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CONNECTICUT STORRS, CONNECTICUT, USA E-mail:[email protected]
ANTONIO MONTALBÁN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY CALIFORNIA-BERKELEY BERKELEY, CALIFORNIA, USA E-mail:[email protected]
REED SOLOMON
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CONNECTICUT STORRS, CONNECTICUT, USA E-mail:[email protected]
LINDA BROWN WESTRICK
Affiliation:
DEPARTMENT OF MATHEMATICS PENN STATE UNIVERSITY UNIVERSITY PARK, PENNSYLVANIA, USA E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We define the notion of a completely determined Borel code in reverse mathematics, and consider the principle 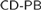$CD - PB$, which states that every completely determined Borel set has the property of Baire. We show that this principle is strictly weaker than 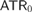$AT{R_0}$. Any ω-model of 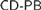$CD - PB$ must be closed under hyperarithmetic reduction, but 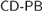$CD - PB$ is not a theory of hyperarithmetic analysis. We show that whenever 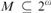$M \subseteq {2^\omega }$ is the second-order part of an ω-model of 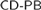$CD - PB$, then for every 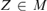$Z \in M$, there is a 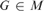$G \in M$ such that G is 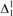${\rm{\Delta }}_1^1$-generic relative to Z.

Keywords

03F35reverse mathematicsBorel setsproperty of Bairedual Ramsey theoremtheories of hyperarithmetic analysis
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 166 - 198
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Blass, A. R., Hirst, J. L., and Simpson, S. G., Logical analysis of some theorems of combinatorics and topological dynamics, Logic and Combinatorics (Arcata, Calif., 1985) (Simpson, S. G., editor), Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, RI, 1987, pp. 125–156.CrossRefGoogle Scholar
Carlson, T. J. and Simpson, S. G., A dual form of Ramsey’s theorem. Advances in Mathematics, vol. 53 (1984), no. 3, pp. 265–290.CrossRefGoogle Scholar
Conidis, C. J., Comparing theorems of hyperarithmetic analysis with the arithmetic Bolzano-Weierstrass theorem. Transactions of the American Mathematical Society, vol. 364 (2012), no. 9, pp. 4465–4494.CrossRefGoogle Scholar
Downey, R. G. and Hirschfeldt, D. R., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer, New York, 2010.CrossRefGoogle Scholar
Dzhafarov, D., Flood, S., Solomon, R., and Westrick, L. B., Effectiveness for the Dual Ramsey Theorem, submitted, 2017. Available arXiv:1710.00070.Google Scholar
Friedman, H., Some systems of second order arithmetic and their use, Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974) (James, R. D., editor), vol. 1, Canadian Mathematical Congress, Ottawa, 1975, pp. 235–242.Google Scholar
Greenberg, N. and Monin, B., Higher randomness and genericity. Forum of Mathematics, Sigma, vol. 5 (2017), pp. e31, 41.CrossRefGoogle Scholar
Harrison, J., Recursive pseudo-well-orderings. Transactions of the American Mathematical Society, vol. 131 (1968), pp. 526–543.CrossRefGoogle Scholar
Jockusch, C. G. Jr., Uniformly introreducible sets, this Journal, vol. 33 (1968), pp. 521–536.Google Scholar
Montalbán, A., Indecomposable linear orderings and hyperarithmetic analysis. Journal of Mathematical Logic, vol. 6 (2006), no. 1, pp. 89–120.CrossRefGoogle Scholar
Montalbán, A., Theories of hyperarithmetic analysis. Slides from talk at the conference in honor of the 60th birthday of Harvey Friedman, 2009.Google Scholar
Prömel, H. J. and Voigt, B., Baire sets of k-parameter words are Ramsey. Transactions of the American Mathematical Society, vol. 291 (1985), no. 1, pp. 189–201.Google Scholar
Rogers, H. Jr., Theory of Recursive Functions and Effective Computability, second ed., MIT Press, Cambridge, MA, 1987.Google Scholar
Sacks, G. E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, second ed., Perspectives in Logic, Cambridge University Press, Cambridge; Association for Symbolic Logic, Poughkeepsie, NY, 2009.CrossRefGoogle Scholar
Steel, J. R., Forcing with tagged trees. Annals of Mathematical Logic, vol. 15 (1978), no. 1, pp. 55–74.CrossRefGoogle Scholar
Van Wesep, R. A., Subsystems of second-order arithmetic, and descriptive set theory under the axiom of determinateness, Ph.D. thesis, University of California, Berkeley, ProQuest LLC, Ann Arbor, MI, 1977.Google Scholar
Yu, L., Lowness for genericity. Archive for Mathematical Logic, vol. 45 (2006), no. 2, pp. 233–238.CrossRefGoogle Scholar