No CrossRef data available.
Article contents
DETERMINACY OF SCHMIDT’S GAME AND OTHER INTERSECTION GAMES
Published online by Cambridge University Press: 30 May 2022
Abstract
Schmidt’s game and other similar intersection games have played an important role in recent years in applications to number theory, dynamics, and Diophantine approximation theory. These games are real games, that is, games in which the players make moves from a complete separable metric space. The determinacy of these games trivially follows from the axiom of determinacy for real games,
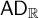 $\mathsf {AD}_{\mathbb R}$
, which is a much stronger axiom than that asserting all integer games are determined,
$\mathsf {AD}_{\mathbb R}$
, which is a much stronger axiom than that asserting all integer games are determined,
 $\mathsf {AD}$
. One of our main results is a general theorem which under the hypothesis
$\mathsf {AD}$
. One of our main results is a general theorem which under the hypothesis
 $\mathsf {AD}$
implies the determinacy of intersection games which have a property allowing strategies to be simplified. In particular, we show that Schmidt’s
$\mathsf {AD}$
implies the determinacy of intersection games which have a property allowing strategies to be simplified. In particular, we show that Schmidt’s
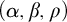 $(\alpha ,\beta ,\rho )$
game on
$(\alpha ,\beta ,\rho )$
game on
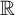 $\mathbb R$
is determined from
$\mathbb R$
is determined from
 $\mathsf {AD}$
alone, but on
$\mathsf {AD}$
alone, but on
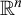 $\mathbb R^n$
for
$\mathbb R^n$
for
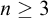 $n \geq 3$
we show that
$n \geq 3$
we show that
 $\mathsf {AD}$
does not imply the determinacy of this game. We then give an application of simple strategies and prove that the winning player in Schmidt’s
$\mathsf {AD}$
does not imply the determinacy of this game. We then give an application of simple strategies and prove that the winning player in Schmidt’s
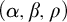 $(\alpha , \beta , \rho )$
game on
$(\alpha , \beta , \rho )$
game on
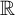 $\mathbb {R}$
has a winning positional strategy, without appealing to the axiom of choice. We also prove several other results specifically related to the determinacy of Schmidt’s game. These results highlight the obstacles in obtaining the determinacy of Schmidt’s game from
$\mathbb {R}$
has a winning positional strategy, without appealing to the axiom of choice. We also prove several other results specifically related to the determinacy of Schmidt’s game. These results highlight the obstacles in obtaining the determinacy of Schmidt’s game from
 $\mathsf {AD}$
.
$\mathsf {AD}$
.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



