Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T11:56:53.979Z Has data issue: false hasContentIssue false
  • English
  • Français

Determinacy in strong cardinal models

Published online by Cambridge University Press:  12 March 2014

P. D. Welch
P. D. Welch*
Affiliation:
School of Mathematics, University of Bristol, Bristol, BS8 1TW, UK, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give limits defined in terms of abstract pointclasses of the amount of determinacy available in certain canonical inner models involving strong cardinals. We show for example:

Theorem A. Det(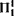-IND) ⇒ there exists an inner model with a strong cardinal.

Theorem B. Det(AQI) ⇒ there exist type-l mice and hence inner models with proper classes of strong cardinals.

where 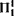-IND(AQI) is the pointclass of boldface 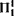-inductive (respectively arithmetically quasi-inductive) sets of reals.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 2 , June 2011 , pp. 719 - 728
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aczel, P. and Richter, W., Inductive definitions and reflecting properties of admissible ordinals. Generalised recursion theory (Proceedings of the Symposium, Oslo, 1972), Studies in Logic and the Foundation of Mathematics, vol. 79, North-Holland, Amsterdam, 1974, pp. 301–381.Google Scholar
[2]Burgess, J. P., The truth is never simple, this Journal, vol. 51 (1986), no. 3, pp. 663–681.Google Scholar
[3]Feng, Q. and Jensen, R.B., Supercomplete extenders and type 1 mice. Annals of Pure and Applied Logic, vol. 128 (2004), no. 1–3, pp. 1–73.CrossRefGoogle Scholar
[4]Friedman, S. D. and Welch, P. D., Hypermachines, this Journal, (2011).Google Scholar
[5]Harrington, L., Analytic determinacy and 0#, this Journal, vol. 43 (1978), no. 4, pp. 684–693.Google Scholar
[6]Kechris, A. S., Forcing in analysis, Higher set theory (Müller, G. and Scott, D., editors), Lecture Notes in Mathematics, vol. 669, Springer, pp. 272–302.Google Scholar
[7]Moschovakis, Y. N., Descriptive set theory, Studies in Logic, North-Holland, Amsterdam, 1980.Google Scholar
[8]Schindler, R-D., The core model for almost linear iterations, Annals of Pure and Applied Logic, (2002), pp. 205–272.Google Scholar
[9]Steel, J. R., Determinacy in the Mitchell models, Annals of Mathematical Logic, vol. 22 (1980), pp. 109–125.CrossRefGoogle Scholar
[10]Steel, J. R., The core model iterability problem, Lecture Notes in Mathematical Logic, vol. 8, Springer, 1996.Google Scholar
[11]Steel, J. R. and Welch, P. D., Σ31-absoluteness and the second uniform indiscernible, Israel Journal of Mathematics, vol. 104 (1998), pp. 157–190.CrossRefGoogle Scholar
[12]Welch, P. D., The length of infinite time Turing machine computations, The Bulletin of the London Mathematical Society, vol. 32 (2000), pp. 129–136.CrossRefGoogle Scholar
[13]Welch, P. D., Post's and other problems in higher type supertasks, Classical and new paradigms of computation and their complexity hierarchies (Lowe, B., Piwinger, B., and Räsch, T., editors), Trends in logic, vol. 23, Kluwer, 2004, papers of the conference Foundations ofthe Formal Sciences III, pp. 223–237.CrossRefGoogle Scholar