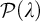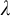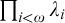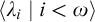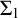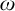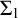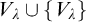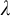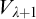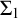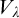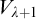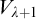1 Introduction
Fundamental results of descriptive set theory show that simply definable sets of real numbers, e.g., Borel sets, possess a rich and canonical structure theory and these structural results have various applications in other areas of mathematics. Moreover, seminal results show that canonical extensions of the axioms of
![]() $\operatorname {\mathrm {ZFC}}$
allow us to extend these structural conclusions to much larger classes of definable sets of reals. Since the developed theory is limited to the study of mathematical objects that can be encoded as definable sets of real numbers, there has been a recent interest to develop a generalized descriptive set theory that allows the study of definable objects of much higher cardinalities. While it is already known that several key results of the classical theory cannot be directly generalized to all higher cardinalities (see, for example, [Reference Lücke and Schlicht14]), the research conducted so far in this area isolated several settings in which rich structure theories for definable sets of higher cardinalities can be developed. The work presented in this paper contributes to the study of one of these settings that originates in Hugh Woodin‘s work on large cardinal assumptions close to the Kunen Inconsistency (see [Reference Hugh Woodin18]).
$\operatorname {\mathrm {ZFC}}$
allow us to extend these structural conclusions to much larger classes of definable sets of reals. Since the developed theory is limited to the study of mathematical objects that can be encoded as definable sets of real numbers, there has been a recent interest to develop a generalized descriptive set theory that allows the study of definable objects of much higher cardinalities. While it is already known that several key results of the classical theory cannot be directly generalized to all higher cardinalities (see, for example, [Reference Lücke and Schlicht14]), the research conducted so far in this area isolated several settings in which rich structure theories for definable sets of higher cardinalities can be developed. The work presented in this paper contributes to the study of one of these settings that originates in Hugh Woodin‘s work on large cardinal assumptions close to the Kunen Inconsistency (see [Reference Hugh Woodin18]).
Remember that a non-trivial elementary embedding
![]() ${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
for some ordinal
${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
for some ordinal
![]() $\lambda $
is an I0-embedding if
$\lambda $
is an I0-embedding if
![]() ${\mathrm {{crit}}({j})}<\lambda $
holds. Kunen’s analysis of elementary embeddings in [Reference Kunen10] then directly shows that
${\mathrm {{crit}}({j})}<\lambda $
holds. Kunen’s analysis of elementary embeddings in [Reference Kunen10] then directly shows that
![]() $\lambda =\sup _{n<\omega }\lambda _n$
holds for every I0-embedding
$\lambda =\sup _{n<\omega }\lambda _n$
holds for every I0-embedding
![]() ${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
with critical sequenceFootnote
1
${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
with critical sequenceFootnote
1
![]() $\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
. Embeddings of this type produce a setting in which descriptive concepts can be developed fruitfully. More specifically, several deep results show that the structural properties of the collection of subsets of
$\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
. Embeddings of this type produce a setting in which descriptive concepts can be developed fruitfully. More specifically, several deep results show that the structural properties of the collection of subsets of
![]() ${\mathcal {P}}({\lambda })$
contained in
${\mathcal {P}}({\lambda })$
contained in
![]() $L(V_{\lambda +1})$
strongly resembles the behavior of the collection of sets of reals in
$L(V_{\lambda +1})$
strongly resembles the behavior of the collection of sets of reals in
![]() $L(\mathbb {R})$
in the presence of the Axiom of Determinacy
$L(\mathbb {R})$
in the presence of the Axiom of Determinacy
![]() $\operatorname {\mathrm {AD}}$
in
$\operatorname {\mathrm {AD}}$
in
![]() $L(\mathbb {R})$
. In the following, we will focus on generalizations of the Perfect Set Property to definable subsets of higher power sets. Given a non-empty set X and an infinite cardinal
$L(\mathbb {R})$
. In the following, we will focus on generalizations of the Perfect Set Property to definable subsets of higher power sets. Given a non-empty set X and an infinite cardinal
![]() $\mu $
, we equip the set
$\mu $
, we equip the set
![]() ${}^\mu X$
of all functions from
${}^\mu X$
of all functions from
![]() $\mu $
to X with the topology whose basic open sets consists of all functions that extend a given function
$\mu $
to X with the topology whose basic open sets consists of all functions that extend a given function
![]() ${s}:{\xi }\longrightarrow {X}$
with
${s}:{\xi }\longrightarrow {X}$
with
![]() $\xi <\mu $
. In addition, we equip the set
$\xi <\mu $
. In addition, we equip the set
![]() ${\mathcal {P}}({\nu })$
of all subsets of an infinite cardinal
${\mathcal {P}}({\nu })$
of all subsets of an infinite cardinal
![]() $\nu $
with the topology whose basic open sets consist of all subsets of
$\nu $
with the topology whose basic open sets consist of all subsets of
![]() $\nu $
whose intersection with a given ordinal
$\nu $
whose intersection with a given ordinal
![]() $\eta <\nu $
is equal to a fixed subset of
$\eta <\nu $
is equal to a fixed subset of
![]() $\eta $
. Finally, we say that a map
$\eta $
. Finally, we say that a map
![]() ${\iota }:{X}\longrightarrow {Y}$
between topological spaces is a perfect embedding if it induces a homeomorphism between X and the subspace
${\iota }:{X}\longrightarrow {Y}$
between topological spaces is a perfect embedding if it induces a homeomorphism between X and the subspace
![]() ${\mathrm {{ran}}(\iota )}$
of Y.
${\mathrm {{ran}}(\iota )}$
of Y.
It is easy to see that for every infinite cardinal
![]() $\lambda $
, there is a subset of
$\lambda $
, there is a subset of
![]() ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
![]() $\lambda $
that does not contain the range of a perfect embedding of
$\lambda $
that does not contain the range of a perfect embedding of
![]() ${}^{{\mathrm {{cof}}({\lambda })}}\lambda $
into
${}^{{\mathrm {{cof}}({\lambda })}}\lambda $
into
![]() ${\mathcal {P}}({\lambda })$
.Footnote
2
In contrast, classical results show that if
${\mathcal {P}}({\lambda })$
.Footnote
2
In contrast, classical results show that if
![]() $\operatorname {\mathrm {AD}}$
holds in
$\operatorname {\mathrm {AD}}$
holds in
![]() $L(\mathbb {R})$
, then every uncountable subset of
$L(\mathbb {R})$
, then every uncountable subset of
![]() ${\mathcal {P}}({\omega })$
in
${\mathcal {P}}({\omega })$
in
![]() $L(\mathbb {R})$
contains the range of a perfect embedding of
$L(\mathbb {R})$
contains the range of a perfect embedding of
![]() ${}^\omega \omega $
into
${}^\omega \omega $
into
![]() ${\mathcal {P}}({\omega })$
. The work of Hugh Woodin, Xianghui Shi, and Scott Cramer now shows that I0-embeddings imply an analogous dichotomy at the supremum of the corresponding critical sequence (see [Reference Cramer1, Section 5], [Reference Shi16, Section 4], and [Reference Hugh Woodin18, Section 7]).
${\mathcal {P}}({\omega })$
. The work of Hugh Woodin, Xianghui Shi, and Scott Cramer now shows that I0-embeddings imply an analogous dichotomy at the supremum of the corresponding critical sequence (see [Reference Cramer1, Section 5], [Reference Shi16, Section 4], and [Reference Hugh Woodin18, Section 7]).
Theorem 1.1 [Reference Cramer1].
If
![]() ${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
is an I0-embedding and X is a subset of
${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
is an I0-embedding and X is a subset of
![]() ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
![]() $\lambda $
that is an element of
$\lambda $
that is an element of
![]() $L(V_{\lambda +1})$
, then there is a perfect embedding
$L(V_{\lambda +1})$
, then there is a perfect embedding
![]() ${\iota }:{{}^\omega \lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
${\iota }:{{}^\omega \lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
![]() ${\mathrm {{ran}}(\iota )}\subseteq X$
.
${\mathrm {{ran}}(\iota )}\subseteq X$
.
The work presented in this paper is motivated by the question whether the restriction of this implication to smaller classes of definable sets can be derived from weaker large cardinal assumptions. It is motivated by the results of Sandra Müller and the third author in [Reference Lücke and Müller13] that analyze simply definable sets at limits of measurable cardinals. In the following, we say a class C is definable by a formula
![]() $\varphi (v_0,\ldots ,v_n)$
and parameters
$\varphi (v_0,\ldots ,v_n)$
and parameters
![]() $z_0,\ldots ,z_{n-1}$
if
$z_0,\ldots ,z_{n-1}$
if
![]() $C=\{{y}~\vert ~{\varphi (y,z_0,\ldots ,z_{n-1})}\}$
holds. We now distinguish classes of definable sets using the Levy hierarchy of formulas
Footnote
3
and the rank of parameters. The following result is the starting point of our work.
$C=\{{y}~\vert ~{\varphi (y,z_0,\ldots ,z_{n-1})}\}$
holds. We now distinguish classes of definable sets using the Levy hierarchy of formulas
Footnote
3
and the rank of parameters. The following result is the starting point of our work.
Theorem 1.2 [Reference Lücke and Müller13].
If
![]() $\lambda $
is a limit of measurable cardinals and X is a subset of
$\lambda $
is a limit of measurable cardinals and X is a subset of
![]() ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
![]() $\lambda $
that is definable by a
$\lambda $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $V_\lambda \cup \{\lambda \}$
, then there is a perfect embedding
$V_\lambda \cup \{\lambda \}$
, then there is a perfect embedding
![]() ${\iota }:{{}^{{\mathrm {{cof}}({\lambda })}}\lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
${\iota }:{{}^{{\mathrm {{cof}}({\lambda })}}\lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
![]() ${\mathrm {{ran}}(\iota )}\subseteq X$
.
${\mathrm {{ran}}(\iota )}\subseteq X$
.
Given an infinite cardinal
![]() $\lambda $
, the
$\lambda $
, the
![]() $\Sigma _1$
-Reflection Principle shows that all
$\Sigma _1$
-Reflection Principle shows that all
![]() $\Sigma _1$
-formulas with parameters in
$\Sigma _1$
-formulas with parameters in
![]() ${H}_{{\lambda ^+}}$
are absolute between V and
${H}_{{\lambda ^+}}$
are absolute between V and
![]() ${H}_{{\lambda ^+}}$
. Therefore, it follows that a subset of
${H}_{{\lambda ^+}}$
. Therefore, it follows that a subset of
![]() ${H}_{{\lambda ^+}}$
is definable by a
${H}_{{\lambda ^+}}$
is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${H}_{{\lambda ^+}}$
if and only if the given set is definable in this way in
${H}_{{\lambda ^+}}$
if and only if the given set is definable in this way in
![]() ${H}_{{\lambda ^+}}$
. This shows that, if
${H}_{{\lambda ^+}}$
. This shows that, if
![]() $\lambda $
is an infinite cardinal with
$\lambda $
is an infinite cardinal with
![]() ${H}_{{\lambda }}=V_\lambda $
, then
${H}_{{\lambda }}=V_\lambda $
, then
![]() $L(V_{\lambda +1})$
contains all subsets of
$L(V_{\lambda +1})$
contains all subsets of
![]() ${\mathcal {P}}({\lambda })$
that are definable by a
${\mathcal {P}}({\lambda })$
that are definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() ${H}_{{\lambda ^+}}$
, because
${H}_{{\lambda ^+}}$
, because
![]() ${H}_{{\lambda ^+}}$
is contained in
${H}_{{\lambda ^+}}$
is contained in
![]() $L(V_{\lambda +1})$
. In particular, it follows that the conclusion of the implication stated in Theorem 1.1 directly implies the conclusion of the implication stated in Theorem 1.2.
$L(V_{\lambda +1})$
. In particular, it follows that the conclusion of the implication stated in Theorem 1.1 directly implies the conclusion of the implication stated in Theorem 1.2.
The theorems cited above directly raise the question if stronger perfect set theorems can be proven for limits of countably many measurable cardinals. In particular, it is natural to ask if the implication of Theorem 1.2 still holds true if we allow more elements of
![]() ${\mathcal {P}}({\lambda })$
in our
${\mathcal {P}}({\lambda })$
in our
![]() $\Sigma _1$
-definitions. A natural candidate for such an additional parameter in
$\Sigma _1$
-definitions. A natural candidate for such an additional parameter in
![]() ${\mathcal {P}}({\lambda })\setminus (V_\lambda \cup \{\lambda \})$
is an
${\mathcal {P}}({\lambda })\setminus (V_\lambda \cup \{\lambda \})$
is an
![]() $\omega $
-sequence of measurable cardinals that is cofinal in the given supremum
$\omega $
-sequence of measurable cardinals that is cofinal in the given supremum
![]() $\lambda $
. Our first result, proven in Section 2, shows that we no longer get a provable implication if we are allowed to use such a sequence as a parameter in our
$\lambda $
. Our first result, proven in Section 2, shows that we no longer get a provable implication if we are allowed to use such a sequence as a parameter in our
![]() $\Sigma _1$
-definitions:
$\Sigma _1$
-definitions:
Theorem 1.3. If
![]() $\vec {\lambda }$
is a strictly increasing sequence of measurable cardinals with limit
$\vec {\lambda }$
is a strictly increasing sequence of measurable cardinals with limit
![]() $\lambda $
, then the following statements hold in an inner model M containing
$\lambda $
, then the following statements hold in an inner model M containing
![]() $\vec {\lambda }$
:
$\vec {\lambda }$
:
-
(i) The sequence
 $\vec {\lambda }$
consists of measurable cardinals.
$\vec {\lambda }$
consists of measurable cardinals. -
(ii) If
 $\vec {\nu }$
is a strictly increasing
$\vec {\nu }$
is a strictly increasing
 $\omega $
-sequence of regular cardinals with limit
$\omega $
-sequence of regular cardinals with limit
 $\lambda $
, then there is a subset of
$\lambda $
, then there is a subset of
 ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
 $\lambda $
that does not contain the range of a perfect embedding of
$\lambda $
that does not contain the range of a perfect embedding of
 ${}^\omega \lambda $
into
${}^\omega \lambda $
into
 ${\mathcal {P}}({\lambda })$
and is definable by a
${\mathcal {P}}({\lambda })$
and is definable by a
 $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
 $V_\lambda \cup \{\vec {\nu }\}$
.
$V_\lambda \cup \{\vec {\nu }\}$
.
We now proceed by showing that a large cardinal axiom strictly weaker than the existence of an I0-embedding implies the perfect set property discussed above. Remember that an elementary embedding
![]() ${j}:{V}\longrightarrow {M}$
with critical sequence
${j}:{V}\longrightarrow {M}$
with critical sequence
![]() $\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
is an I2-embedding if
$\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
is an I2-embedding if
![]() $V_\lambda \subseteq M$
, where
$V_\lambda \subseteq M$
, where
![]() $\lambda =\sup _{n<\omega }\lambda _n$
. The existence of such an embedding is equivalent to the existence of a non-trivial elementary embedding
$\lambda =\sup _{n<\omega }\lambda _n$
. The existence of such an embedding is equivalent to the existence of a non-trivial elementary embedding
![]() ${i}:{V_\lambda }\longrightarrow {V_\lambda }$
with critical sequence
${i}:{V_\lambda }\longrightarrow {V_\lambda }$
with critical sequence
![]() $\langle {\nu _n}~\vert ~{n<\omega }\rangle $
such that
$\langle {\nu _n}~\vert ~{n<\omega }\rangle $
such that
![]() $\lambda =\sup _{n<\omega }\nu _n$
and the canonical map
$\lambda =\sup _{n<\omega }\nu _n$
and the canonical map
extending i to
![]() $V_{\lambda +1}$
maps well-founded relations on
$V_{\lambda +1}$
maps well-founded relations on
![]() $V_\lambda $
to well-founded relations on
$V_\lambda $
to well-founded relations on
![]() $V_\lambda $
(see [Reference Kanamori9, Proposition 24.2]). The results of [Reference Laver11] show that, if
$V_\lambda $
(see [Reference Kanamori9, Proposition 24.2]). The results of [Reference Laver11] show that, if
![]() ${i}:{L(V_{\nu +1})}\longrightarrow {L(V_{\nu +1})}$
is an I0-embedding, then there is an embedding
${i}:{L(V_{\nu +1})}\longrightarrow {L(V_{\nu +1})}$
is an I0-embedding, then there is an embedding
![]() ${j}:{V_\lambda }\longrightarrow {V_\lambda }$
for some
${j}:{V_\lambda }\longrightarrow {V_\lambda }$
for some
![]() $\lambda <\nu $
with the given property. Since
$\lambda <\nu $
with the given property. Since
![]() $\nu $
is a limit of inaccessible cardinals in this setting, it follows that the existence of an I0-embedding has strictly higher consistency strength than the existence of an I2-embedding. The next result, proven in Section 3, shows that I2-embeddings imply the desired perfect set property.
$\nu $
is a limit of inaccessible cardinals in this setting, it follows that the existence of an I0-embedding has strictly higher consistency strength than the existence of an I2-embedding. The next result, proven in Section 3, shows that I2-embeddings imply the desired perfect set property.
Theorem 1.4. Let
![]() ${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and set
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and set
![]() $\lambda =\sup _{n<\omega }{\lambda _n}$
. If X is a subset of
$\lambda =\sup _{n<\omega }{\lambda _n}$
. If X is a subset of
![]() ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
![]() $\lambda $
that is definable by a
$\lambda $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $V_\lambda \cup \{V_\lambda ,\vec {\lambda }\}$
, then there is a perfect embedding
$V_\lambda \cup \{V_\lambda ,\vec {\lambda }\}$
, then there is a perfect embedding
![]() ${\iota }:{{}^\omega \lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
${\iota }:{{}^\omega \lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
![]() ${\mathrm {{ran}}(\iota )}\subseteq X$
.
${\mathrm {{ran}}(\iota )}\subseteq X$
.
The proof of this theorem will show that its conclusion holds for subsets of
![]() ${\mathcal {P}}({\lambda })$
that are definable from a significantly larger set of parameters in
${\mathcal {P}}({\lambda })$
that are definable from a significantly larger set of parameters in
![]() $V_{\lambda +1}$
(see Theorem 3.1 below). However, in Section 2, we will observe that an assumption strictly stronger than the existence of an I2-embedding is necessary to obtain this perfect set property for all subsets of
$V_{\lambda +1}$
(see Theorem 3.1 below). However, in Section 2, we will observe that an assumption strictly stronger than the existence of an I2-embedding is necessary to obtain this perfect set property for all subsets of
![]() ${\mathcal {P}}({\lambda })$
that are definable by
${\mathcal {P}}({\lambda })$
that are definable by
![]() $\Sigma _1$
-formulas with parameters in
$\Sigma _1$
-formulas with parameters in
![]() ${\mathcal {P}}({\lambda })$
.
${\mathcal {P}}({\lambda })$
.
Theorem 1.5. If
![]() ${j}:{V}\longrightarrow {M}$
is an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
is an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and
![]() $\lambda =\sup _{n<\omega }\lambda _n$
, then the following statements hold in an inner model:
$\lambda =\sup _{n<\omega }\lambda _n$
, then the following statements hold in an inner model:
-
(i) There is an I2-embedding whose critical sequence has supremum
 $\lambda $
.
$\lambda $
. -
(ii) There is a subset z of
 $\lambda $
and a subset X of
$\lambda $
and a subset X of
 ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
 $\lambda $
such that X does not contain the range of a perfect embedding of
$\lambda $
such that X does not contain the range of a perfect embedding of
 ${}^\omega \lambda $
into
${}^\omega \lambda $
into
 ${\mathcal {P}}({\lambda })$
and the set X is definable by a
${\mathcal {P}}({\lambda })$
and the set X is definable by a
 $\Sigma _1$
-formula with parameter z.
$\Sigma _1$
-formula with parameter z.
The five results discussed above suggest the intriguing possibility of studying large cardinal assumptions canonically inducing singular cardinals
![]() $\lambda $
of countable cofinality through the provable regularity properties of simply definable subsets of
$\lambda $
of countable cofinality through the provable regularity properties of simply definable subsets of
![]() ${\mathcal {P}}({\lambda })$
. More specifically, they suggest that for each large cardinal axiom of this form, we want to uniformly assign as large subsets
${\mathcal {P}}({\lambda })$
. More specifically, they suggest that for each large cardinal axiom of this form, we want to uniformly assign as large subsets
![]() $P_\lambda $
of
$P_\lambda $
of
![]() $V_{\lambda +1}$
as possible to each singular cardinal
$V_{\lambda +1}$
as possible to each singular cardinal
![]() $\lambda $
, in a way that ensures that
$\lambda $
, in a way that ensures that
![]() $\operatorname {\mathrm {ZFC}}$
proves that whenever
$\operatorname {\mathrm {ZFC}}$
proves that whenever
![]() $\lambda $
is a singular cardinal of countable cofinality induced by a cardinal of the given type, then all subsets of
$\lambda $
is a singular cardinal of countable cofinality induced by a cardinal of the given type, then all subsets of
![]() ${\mathcal {P}}({\lambda })$
that are definable by
${\mathcal {P}}({\lambda })$
that are definable by
![]() $\Sigma _1$
-formulas using parameters from
$\Sigma _1$
-formulas using parameters from
![]() $P_\lambda $
either have cardinality at most
$P_\lambda $
either have cardinality at most
![]() $\lambda $
or contain the range of a perfect embedding of
$\lambda $
or contain the range of a perfect embedding of
![]() ${}^\omega \lambda $
into
${}^\omega \lambda $
into
![]() ${\mathcal {P}}({\lambda })$
. Note that, since this approach is based on provable implications and not consistency strength, it is less affected by the current technical limitations of inner model theory and therefore provides a new angle to study strong large cardinal axioms.
${\mathcal {P}}({\lambda })$
. Note that, since this approach is based on provable implications and not consistency strength, it is less affected by the current technical limitations of inner model theory and therefore provides a new angle to study strong large cardinal axioms.
In addition to
![]() $\Sigma _1$
-definable subsets of power sets, we will also study spaces and complexity classes that more closely resemble the objects studied in classical descriptive set theory. More specifically, for a given strictly increasing sequence
$\Sigma _1$
-definable subsets of power sets, we will also study spaces and complexity classes that more closely resemble the objects studied in classical descriptive set theory. More specifically, for a given strictly increasing sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of infinite cardinals with supremum
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of infinite cardinals with supremum
![]() $\lambda $
, we will study subsets of the closed subspace
$\lambda $
, we will study subsets of the closed subspace
![]() $C(\vec {\lambda })$
of
$C(\vec {\lambda })$
of
![]() ${}^\omega \lambda $
consisting of all functions in the set
${}^\omega \lambda $
consisting of all functions in the set
![]() $\prod _{n<\omega }\lambda _n$
, i.e., all functions
$\prod _{n<\omega }\lambda _n$
, i.e., all functions
![]() ${x}:{\omega }\longrightarrow {\lambda }$
satisfying
${x}:{\omega }\longrightarrow {\lambda }$
satisfying
![]() $x(n)<\lambda _n$
for all
$x(n)<\lambda _n$
for all
![]() $n<\omega $
. Note that the map
$n<\omega $
. Note that the map
yields a homeomorphism between
![]() $C(\vec {\lambda })$
and a closed subset of
$C(\vec {\lambda })$
and a closed subset of
![]() ${\mathcal {P}}({\lambda })$
.Footnote
4
Moreover, since the map
${\mathcal {P}}({\lambda })$
.Footnote
4
Moreover, since the map
![]() $\iota _{\vec {\lambda }}$
is definable by a
$\iota _{\vec {\lambda }}$
is definable by a
![]() $\Delta _0$
-formula with parameter
$\Delta _0$
-formula with parameter
![]() $\vec {\lambda }$
, Theorem 1.4 immediately implies a perfect set theorem for subsets of
$\vec {\lambda }$
, Theorem 1.4 immediately implies a perfect set theorem for subsets of
![]() $C(\vec {\lambda })$
definable by
$C(\vec {\lambda })$
definable by
![]() $\Sigma _1$
-formulas with parameters in the set
$\Sigma _1$
-formulas with parameters in the set
![]() $V_\lambda \cup \{\vec {\lambda }\}$
. Finally, the sets produced in the proofs of Theorems 1.3 and 1.5 will actually be subsets of
$V_\lambda \cup \{\vec {\lambda }\}$
. Finally, the sets produced in the proofs of Theorems 1.3 and 1.5 will actually be subsets of
![]() ${\mathrm {{ran}}(\iota _{\vec {\lambda }})}$
and therefore yield analogous negative results for
${\mathrm {{ran}}(\iota _{\vec {\lambda }})}$
and therefore yield analogous negative results for
![]() $\Sigma _1$
-definable subsets of
$\Sigma _1$
-definable subsets of
![]() $C(\vec {\lambda })$
(see Theorems 2.3 and 2.4 below).
$C(\vec {\lambda })$
(see Theorems 2.3 and 2.4 below).
The theorems above extends beyond
![]() ${\mathcal {P}}({\lambda })$
and
${\mathcal {P}}({\lambda })$
and
![]() $C(\vec {\lambda })$
: In [Reference Dimonte and Ros4] a whole classes of spaces is introduced: the
$C(\vec {\lambda })$
: In [Reference Dimonte and Ros4] a whole classes of spaces is introduced: the
![]() $\lambda $
-Polish spaces, i.e., spaces that are completely metrizable and with weight
$\lambda $
-Polish spaces, i.e., spaces that are completely metrizable and with weight
![]() $\lambda $
, and it is easy to prove analogous results for them. For example,
$\lambda $
, and it is easy to prove analogous results for them. For example,
![]() ${}^{\lambda }{2}$
, with the bounded topology, is homeomorphic to
${}^{\lambda }{2}$
, with the bounded topology, is homeomorphic to
![]() ${\mathcal {P}}({\lambda })$
, and therefore Theorems 1.2, 1.3, 1.4, and 1.5 hold in there. The space
${\mathcal {P}}({\lambda })$
, and therefore Theorems 1.2, 1.3, 1.4, and 1.5 hold in there. The space
![]() ${}^{\omega }{\lambda }$
, with the product topology, is homeomorphic to a closed subset of
${}^{\omega }{\lambda }$
, with the product topology, is homeomorphic to a closed subset of
![]() ${\mathcal {P}}({\lambda })$
via the map
${\mathcal {P}}({\lambda })$
via the map
![]() $x\mapsto {\prec }{n},{x(n)}{\succ }$
, and it contains
$x\mapsto {\prec }{n},{x(n)}{\succ }$
, and it contains
![]() $C(\vec {\lambda })$
as a closed set, therefore Theorems 1.3, 1.4, and 1.5 hold in there. If
$C(\vec {\lambda })$
as a closed set, therefore Theorems 1.3, 1.4, and 1.5 hold in there. If
![]() $(X,d)$
is any
$(X,d)$
is any
![]() $\lambda $
-Polish space, then there is a
$\lambda $
-Polish space, then there is a
![]() $\Sigma _1(d)$
continuous bijection between a closed set
$\Sigma _1(d)$
continuous bijection between a closed set
![]() $F\subseteq {}^{\lambda }{\omega }$
and X ([Reference Dimonte and Ros4]). By pulling back with the bijection, we can therefore prove Theorems 1.2, 1.3, 1.4, and 1.5 also in there. Finally, if d is more complicated, the negative results of Theorems 1.3 and 1.5 hold anyway, but respectively with a witness in
$F\subseteq {}^{\lambda }{\omega }$
and X ([Reference Dimonte and Ros4]). By pulling back with the bijection, we can therefore prove Theorems 1.2, 1.3, 1.4, and 1.5 also in there. Finally, if d is more complicated, the negative results of Theorems 1.3 and 1.5 hold anyway, but respectively with a witness in
![]() $\Sigma _1(V_{\lambda }\cup \{V_\lambda ,\vec {\lambda },d\})$
and in
$\Sigma _1(V_{\lambda }\cup \{V_\lambda ,\vec {\lambda },d\})$
and in
![]() $\Sigma _1(z,d)$
.
$\Sigma _1(z,d)$
.
In another direction, we will not only study subsets of
![]() ${\mathcal {P}}({\lambda })$
,
${\mathcal {P}}({\lambda })$
,
![]() ${}^\omega \lambda $
or
${}^\omega \lambda $
or
![]() $C(\vec {\lambda })$
that are definable in V by formulas of a given complexity, but also sets that are definable over
$C(\vec {\lambda })$
that are definable in V by formulas of a given complexity, but also sets that are definable over
![]() $V_\lambda $
by higher-order formulas in the classes
$V_\lambda $
by higher-order formulas in the classes
![]() $\Sigma ^m_n$
and
$\Sigma ^m_n$
and
![]() $\Pi ^m_n$
(see, for example, [Reference Jech8, p. 295]) using certain parameters contained in
$\Pi ^m_n$
(see, for example, [Reference Jech8, p. 295]) using certain parameters contained in
![]() $V_{\lambda +1}$
. The following results (whose proof is a routine adaptation of the proof of [Reference Jech8, Lemma 25.25] to higher cardinals of countable cofinality) connects this form of definability to
$V_{\lambda +1}$
. The following results (whose proof is a routine adaptation of the proof of [Reference Jech8, Lemma 25.25] to higher cardinals of countable cofinality) connects this form of definability to
![]() $\Sigma _1$
-definitions:
$\Sigma _1$
-definitions:
Proposition 1.6. For every
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_{k-1})$
in the language of set theory, there exists a
$\varphi (v_0,\ldots ,v_{k-1})$
in the language of set theory, there exists a
![]() $\Sigma ^1_2$
-formula
$\Sigma ^1_2$
-formula
![]() $\psi (w_0,\ldots ,w_{k-1})$
in the language of set theory with free second-order parameters
$\psi (w_0,\ldots ,w_{k-1})$
in the language of set theory with free second-order parameters
![]() $w_0,\ldots ,w_{k-1}$
such that
$w_0,\ldots ,w_{k-1}$
such that
![]() $\operatorname {\mathrm {ZFC}}$
proves that
$\operatorname {\mathrm {ZFC}}$
proves that
holds for every singular cardinal
![]() $\lambda $
of countable cofinality with
$\lambda $
of countable cofinality with
![]() ${H}_{{\lambda }}=V_\lambda $
and all
${H}_{{\lambda }}=V_\lambda $
and all
![]() $A_0,\ldots ,A_{k-1}\in V_{\lambda +1}$
.
$A_0,\ldots ,A_{k-1}\in V_{\lambda +1}$
.
We will later show (see Corollary 3.3) that, in certain contexts, it is also possible to translate
![]() $\Sigma ^1_2$
-formulas into
$\Sigma ^1_2$
-formulas into
![]() $\Sigma _1$
-formulas. Moreover, note that, in [Reference Dimonte and Ros4], Luca Motto Ros and the first author prove that, analogous to the classical setting, for every singular strong limit cardinal
$\Sigma _1$
-formulas. Moreover, note that, in [Reference Dimonte and Ros4], Luca Motto Ros and the first author prove that, analogous to the classical setting, for every singular strong limit cardinal
![]() $\lambda $
of countable cofinality, every
$\lambda $
of countable cofinality, every
![]() $\mathbf {\Sigma }^1_1$
-subset of
$\mathbf {\Sigma }^1_1$
-subset of
![]() ${}^\omega \lambda $
(i.e., every subset of
${}^\omega \lambda $
(i.e., every subset of
![]() ${}^\omega \lambda $
that is definable over
${}^\omega \lambda $
that is definable over
![]() $V_\lambda $
by a
$V_\lambda $
by a
![]() $\Sigma _1^1$
-formula with parameters in
$\Sigma _1^1$
-formula with parameters in
![]() $V_{\lambda +1}$
) of cardinality greater than
$V_{\lambda +1}$
) of cardinality greater than
![]() $\lambda $
contains the range of a perfect embedding of
$\lambda $
contains the range of a perfect embedding of
![]() ${}^\omega \lambda $
into itself. In addition, still completely analogous to the classical setting, they show that, if
${}^\omega \lambda $
into itself. In addition, still completely analogous to the classical setting, they show that, if
![]() $V=L$
holds and
$V=L$
holds and
![]() $\lambda $
is a singular cardinal of countable cofinality, then there is a subset of
$\lambda $
is a singular cardinal of countable cofinality, then there is a subset of
![]() ${}^\omega \lambda $
of cardinality
${}^\omega \lambda $
of cardinality
![]() $\lambda ^+$
that is definable over
$\lambda ^+$
that is definable over
![]() $V_\lambda $
by a
$V_\lambda $
by a
![]() $\Pi ^1_1$
-formula without parameters.
$\Pi ^1_1$
-formula without parameters.
In addition, we later will consider an analog of the Baire Property to
![]() $\lambda $
, that we call
$\lambda $
, that we call
![]() $\vec {\mathcal {U}}$
-Baire property (see Definition 4.3 below). In analogy with Theorem 1.4, the existence of an I2-embedding with supremum of the critical sequence
$\vec {\mathcal {U}}$
-Baire property (see Definition 4.3 below). In analogy with Theorem 1.4, the existence of an I2-embedding with supremum of the critical sequence
![]() $\lambda $
implies that every subset of
$\lambda $
implies that every subset of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
that is definable by a
$\operatorname{\mathrm{C}}(\vec{\lambda})$
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $V_\lambda \cup \{V_\lambda ,\vec {\lambda }\}$
has the
$V_\lambda \cup \{V_\lambda ,\vec {\lambda }\}$
has the
![]() $\vec {\mathcal {U}}$
-Baire property (see Theorem 4.12 below). Moreover, in analogy with Theorem 1.1, the existence of an I0-embedding with supremum of the critical sequence
$\vec {\mathcal {U}}$
-Baire property (see Theorem 4.12 below). Moreover, in analogy with Theorem 1.1, the existence of an I0-embedding with supremum of the critical sequence
![]() $\lambda $
implies that every subset of
$\lambda $
implies that every subset of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
in
$\operatorname{\mathrm{C}}(\vec{\lambda})$
in
![]() $L_1(V_{\lambda +1})$
has the
$L_1(V_{\lambda +1})$
has the
![]() $\vec {\mathcal {U}}$
-Baire property (see Theorem 4.14 below). Finally, as a negative result, we show that, in the inner model constructed in the proof of Theorem 1.5, there exists an I2-embedding with supremum of the critical sequence
$\vec {\mathcal {U}}$
-Baire property (see Theorem 4.14 below). Finally, as a negative result, we show that, in the inner model constructed in the proof of Theorem 1.5, there exists an I2-embedding with supremum of the critical sequence
![]() $\lambda $
and a subset of
$\lambda $
and a subset of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
without the
$\operatorname{\mathrm{C}}(\vec{\lambda})$
without the
![]() $\vec {\mathcal {U}}$
-Baire property that is definable by a
$\vec {\mathcal {U}}$
-Baire property that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $V_{\lambda +1}$
(see Theorem 4.10 below).
$V_{\lambda +1}$
(see Theorem 4.10 below).
2 Negative results
In this section, we will prove the restricting results stated in the introduction (Theorems 1.3 and 1.5). Theorem 1.3 motivates the formulation of the main result of this paper (Theorem 1.4) by showing that its conclusion cannot be derived from the weaker large cardinal assumptions used in Theorem 1.2. On the other hand, Theorem 1.5 shows that the statement of Theorem 1.4 cannot be strengthened to affect all sets that are
![]() $\Sigma _1$
-definable from arbitrary subsets of the given singular cardinal. In the following, we use arguments based on ideas and notions that were already used in [Reference Lücke and Müller13, Section 4].
$\Sigma _1$
-definable from arbitrary subsets of the given singular cardinal. In the following, we use arguments based on ideas and notions that were already used in [Reference Lücke and Müller13, Section 4].
Definition 2.1. Let
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of cardinals with supremum
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of cardinals with supremum
![]() $\lambda $
and let
$\lambda $
and let
![]() $\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\lambda }\rangle $
be a sequence of elements of
$\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\lambda }\rangle $
be a sequence of elements of
![]() $V_{\lambda }$
.
$V_{\lambda }$
.
-
(i) Given
 $x\subseteq \lambda $
, we define
$x\subseteq \lambda $
, we define
 $\lhd _x$
to be the unique binary relation on
$\lhd _x$
to be the unique binary relation on
 $\lambda $
with the property that
$\lambda $
with the property that  $$ \begin{align*}\alpha\lhd_x\beta ~ \Longleftrightarrow ~ {\prec}{\alpha},{\beta}{\succ}\in x\end{align*} $$
$$ \begin{align*}\alpha\lhd_x\beta ~ \Longleftrightarrow ~ {\prec}{\alpha},{\beta}{\succ}\in x\end{align*} $$
holds for all
 $\alpha ,\beta <\lambda $
.
$\alpha ,\beta <\lambda $
. -
(ii) We define
 $\mathcal {W}\mathcal {O}_\lambda $
to be the set of all
$\mathcal {W}\mathcal {O}_\lambda $
to be the set of all
 $x\in {\mathcal {P}}({\lambda })$
with the property that
$x\in {\mathcal {P}}({\lambda })$
with the property that
 $\lhd _x$
is a well-ordering of
$\lhd _x$
is a well-ordering of
 $\lambda $
.
$\lambda $
. -
(iii) We let
 $\mathsf {WO}(\vec {\lambda },\vec {a})$
denote the set of all
$\mathsf {WO}(\vec {\lambda },\vec {a})$
denote the set of all
 $b\in {}^\omega \lambda $
with the property that there exists
$b\in {}^\omega \lambda $
with the property that there exists
 $x\in \mathcal {W}\mathcal {O}_\lambda $
such that
$x\in \mathcal {W}\mathcal {O}_\lambda $
such that
 $x\cap \lambda _n=a_{b(n)}$
holds for all
$x\cap \lambda _n=a_{b(n)}$
holds for all
 $n<\omega $
.
$n<\omega $
. -
(iv) Given an element b of
 $\mathsf {WO}(\vec {\lambda },\vec {a})$
, we let
$\mathsf {WO}(\vec {\lambda },\vec {a})$
, we let
 $\|b\|_{\vec {a}}$
denote the order-type of the resulting well-order
$\|b\|_{\vec {a}}$
denote the order-type of the resulting well-order
 $\langle \lambda ,\lhd _{\hspace {0.9pt}\bigcup \{{a_{b(n)}}~\vert ~{n<\omega }\}}\rangle $
.
$\langle \lambda ,\lhd _{\hspace {0.9pt}\bigcup \{{a_{b(n)}}~\vert ~{n<\omega }\}}\rangle $
.
The following Boundedness Lemma now follows from the theory developed in [Reference Lücke and Müller13, Section 4] that generalizes classical arguments from descriptive set theory to singular strong limit cardinals of countable cofinality.
Lemma 2.2 [Reference Lücke and Müller13, Lemma 4.5].
Let
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of inaccessible cardinals with supremum
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of inaccessible cardinals with supremum
![]() $\lambda $
and let
$\lambda $
and let
![]() $\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\lambda }\rangle $
be an enumeration of
$\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\lambda }\rangle $
be an enumeration of
![]() ${H}_{{\lambda }}$
. If
${H}_{{\lambda }}$
. If
![]() ${f}:{{}^\omega \lambda }\longrightarrow {{}^\omega \lambda }$
is a continuous function with
${f}:{{}^\omega \lambda }\longrightarrow {{}^\omega \lambda }$
is a continuous function with
![]() ${\mathrm {{ran}}(f)}\subseteq \mathsf {WO}(\vec {\lambda },\vec {a})$
, then there exists an ordinal
${\mathrm {{ran}}(f)}\subseteq \mathsf {WO}(\vec {\lambda },\vec {a})$
, then there exists an ordinal
![]() $\gamma <\lambda ^+$
with
$\gamma <\lambda ^+$
with
![]() $\|f(c)\|_{\vec {a}}<\gamma $
for all
$\|f(c)\|_{\vec {a}}<\gamma $
for all
![]() $c\in {}^\omega \lambda $
.
$c\in {}^\omega \lambda $
.
We start by limiting the provable structural consequences of I2-embeddings by proving the following strengthening of Theorem 1.5 that shows that the statement of Theorem 1.4 cannot be strengthened to show that the existence of an I2-embedding at a cardinal
![]() $\lambda $
implies that every subset of
$\lambda $
implies that every subset of
![]() ${\mathcal {P}}({\lambda })$
that is definable by a
${\mathcal {P}}({\lambda })$
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $V_{\lambda +1}$
either has cardinality
$V_{\lambda +1}$
either has cardinality
![]() $\lambda $
or contains the range of a perfect embedding:
$\lambda $
or contains the range of a perfect embedding:
Theorem 2.3. If
![]() ${j}:{V}\longrightarrow {M}$
is an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
is an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and
![]() $\lambda =\sup _{n<\omega }\lambda _n$
, then the following statements hold in an inner model:
$\lambda =\sup _{n<\omega }\lambda _n$
, then the following statements hold in an inner model:
-
(i) There is an I2-embedding whose critical sequence has supremum
 $\lambda $
.
$\lambda $
. -
(ii) There is a subset z of
 $\lambda $
and a subset X of
$\lambda $
and a subset X of
 $C(\vec {\lambda })$
of cardinality greater than
$C(\vec {\lambda })$
of cardinality greater than
 $\lambda $
such that X does not contain the range of a perfect embedding of
$\lambda $
such that X does not contain the range of a perfect embedding of
 ${}^\omega \lambda $
into
${}^\omega \lambda $
into
 $C(\vec {\lambda })$
and the set X is definable by a
$C(\vec {\lambda })$
and the set X is definable by a
 $\Sigma _1$
-formula with parameter z.
$\Sigma _1$
-formula with parameter z.
Proof. Since
![]() $\lambda $
is a limit of inaccessible cardinals, we can find a subset y of
$\lambda $
is a limit of inaccessible cardinals, we can find a subset y of
![]() $\lambda $
with the property that
$\lambda $
with the property that
![]() $V_\lambda \cup \{\vec {\lambda }, ~ j\restriction V_\lambda \}\subseteq L[y]$
. Since this setup ensures that
$V_\lambda \cup \{\vec {\lambda }, ~ j\restriction V_\lambda \}\subseteq L[y]$
. Since this setup ensures that
we know that
![]() $(j\restriction V_\lambda )_+^{L[y]}$
maps well-founded relations on
$(j\restriction V_\lambda )_+^{L[y]}$
maps well-founded relations on
![]() $V_\lambda $
in
$V_\lambda $
in
![]() $L[y]$
to well-founded relations on
$L[y]$
to well-founded relations on
![]() $V_\lambda $
in
$V_\lambda $
in
![]() $L[y]$
and it follows that
$L[y]$
and it follows that
![]() $j\restriction V_\lambda $
witnesses that, in
$j\restriction V_\lambda $
witnesses that, in
![]() $L[y]$
, there is an I2-embedding whose critical sequence has supremum
$L[y]$
, there is an I2-embedding whose critical sequence has supremum
![]() $\lambda $
.
$\lambda $
.
Now, work in
![]() $L[y]$
. First, observe that the set
$L[y]$
. First, observe that the set
![]() $\mathcal {W}\mathcal {O}_\lambda $
consists of all subsets x of
$\mathcal {W}\mathcal {O}_\lambda $
consists of all subsets x of
![]() $\lambda $
with the property that there exists an ordinal
$\lambda $
with the property that there exists an ordinal
![]() $\gamma $
and an order isomorphism between
$\gamma $
and an order isomorphism between
![]() $\langle \lambda ,\lhd _x\rangle $
and
$\langle \lambda ,\lhd _x\rangle $
and
![]() $\langle \gamma ,<\rangle $
. In addition, the set
$\langle \gamma ,<\rangle $
. In addition, the set
![]() $\mathcal {W}\mathcal {O}_\lambda $
also consists of all subsets x of
$\mathcal {W}\mathcal {O}_\lambda $
also consists of all subsets x of
![]() $\lambda $
such that
$\lambda $
such that
![]() $\langle \lambda ,\lhd _x\rangle $
is a linear ordering with the property that no injective sequence
$\langle \lambda ,\lhd _x\rangle $
is a linear ordering with the property that no injective sequence
![]() $\langle {\alpha _n}~\vert ~{n<\omega }\rangle $
is decreasing with respect to
$\langle {\alpha _n}~\vert ~{n<\omega }\rangle $
is decreasing with respect to
![]() $\lhd _x$
. This shows that
$\lhd _x$
. This shows that
![]() $\mathcal {W}\mathcal {O}_\lambda $
is
$\mathcal {W}\mathcal {O}_\lambda $
is
![]() $\Delta _1$
-definableFootnote
5
from the parameter
$\Delta _1$
-definableFootnote
5
from the parameter
![]() $\lambda $
. Pick an enumeration
$\lambda $
. Pick an enumeration
![]() $\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\lambda }\rangle $
of
$\vec {a}=\langle {a_\alpha }~\vert ~{\alpha <\lambda }\rangle $
of
![]() $V_\lambda $
with
$V_\lambda $
with
![]() $V_{\lambda _n}=\{{a_\alpha }~\vert ~{\alpha <\lambda _n}\}$
for all
$V_{\lambda _n}=\{{a_\alpha }~\vert ~{\alpha <\lambda _n}\}$
for all
![]() $n<\omega $
. Then there exists an unbounded subset z of
$n<\omega $
. Then there exists an unbounded subset z of
![]() $\lambda $
with the property that the sets
$\lambda $
with the property that the sets
![]() $\{\vec {a}\}$
,
$\{\vec {a}\}$
,
![]() $\{y\}$
and
$\{y\}$
and
![]() $\{\vec {\lambda }\}$
are all definable by
$\{\vec {\lambda }\}$
are all definable by
![]() $\Sigma _1$
-formulas with parameter z. Note that this implies that these sets are actually
$\Sigma _1$
-formulas with parameter z. Note that this implies that these sets are actually
![]() $\Delta _1$
-definable from the parameter z. Note that an element b of
$\Delta _1$
-definable from the parameter z. Note that an element b of
![]() ${}^\omega \lambda $
is not contained in
${}^\omega \lambda $
is not contained in
![]() $\mathsf {WO}(\vec {\lambda },\vec {a})$
if and only if either there are
$\mathsf {WO}(\vec {\lambda },\vec {a})$
if and only if either there are
![]() $m<n<\omega $
with
$m<n<\omega $
with
![]() $a_{b(n)}\cap \lambda _m\neq a_{b(m)}$
or there exists
$a_{b(n)}\cap \lambda _m\neq a_{b(m)}$
or there exists
![]() $x\in {\mathcal {P}}({\lambda })\setminus \mathcal {W}\mathcal {O}_\lambda $
with
$x\in {\mathcal {P}}({\lambda })\setminus \mathcal {W}\mathcal {O}_\lambda $
with
![]() $x\cap \lambda _n=a_{b(n)}$
holds for all
$x\cap \lambda _n=a_{b(n)}$
holds for all
![]() $n<\omega $
. Together with our earlier observations, this shows that the set
$n<\omega $
. Together with our earlier observations, this shows that the set
![]() $\mathsf {WO}(\vec {\lambda },\vec {a})$
is
$\mathsf {WO}(\vec {\lambda },\vec {a})$
is
![]() $\Delta _1$
-definable from the parameter z. Given
$\Delta _1$
-definable from the parameter z. Given
![]() $\lambda \leq \gamma <\lambda ^+$
, we now let
$\lambda \leq \gamma <\lambda ^+$
, we now let
![]() $b_\gamma $
denote the
$b_\gamma $
denote the
![]() $<_{L[y]}$
-least element of
$<_{L[y]}$
-least element of
![]() $\mathsf {WO}(\vec {\lambda },\vec {a})$
with
$\mathsf {WO}(\vec {\lambda },\vec {a})$
with
![]() $\|b_\gamma \|_{\vec {a}}=\gamma $
and
$\|b_\gamma \|_{\vec {a}}=\gamma $
and
![]() $b_\gamma (n)<\lambda _{n+1}$
for all
$b_\gamma (n)<\lambda _{n+1}$
for all
![]() $n<\omega $
. Note that our setup ensures that such a set exists for all
$n<\omega $
. Note that our setup ensures that such a set exists for all
![]() $\lambda \leq \gamma <\lambda ^+$
. Moreover, since the basic structure theory of
$\lambda \leq \gamma <\lambda ^+$
. Moreover, since the basic structure theory of
![]() $L[y]$
ensures that the class of proper initial segments of
$L[y]$
ensures that the class of proper initial segments of
![]() $<_{L[y]}$
is definable by a
$<_{L[y]}$
is definable by a
![]() $\Sigma _1$
-formula with parameter z, the fact that
$\Sigma _1$
-formula with parameter z, the fact that
![]() $\mathsf {WO}(\vec {\lambda },\vec {a})$
is
$\mathsf {WO}(\vec {\lambda },\vec {a})$
is
![]() $\Delta _1$
-definable from the parameter z yields a
$\Delta _1$
-definable from the parameter z yields a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,v_1,v_2)$
with the property that
$\varphi (v_0,v_1,v_2)$
with the property that
![]() $\varphi (\gamma ,b,z)$
holds if and only if
$\varphi (\gamma ,b,z)$
holds if and only if
![]() $\gamma $
is an ordinal in the interval
$\gamma $
is an ordinal in the interval
![]() $[\lambda ,\lambda ^+)$
and
$[\lambda ,\lambda ^+)$
and
![]() $b=b_\gamma $
. Let X denote the set of all
$b=b_\gamma $
. Let X denote the set of all
![]() $b\in {}^\omega \lambda $
with the property that
$b\in {}^\omega \lambda $
with the property that
![]() $b(0)=0$
and there exists
$b(0)=0$
and there exists
![]() $\lambda \leq \gamma <\lambda ^+$
with
$\lambda \leq \gamma <\lambda ^+$
with
![]() $b(n+1)=b_\gamma (n)$
for all
$b(n+1)=b_\gamma (n)$
for all
![]() $n<\omega $
. We then know that X is a subset of
$n<\omega $
. We then know that X is a subset of
![]() $C(\vec {\lambda })$
of cardinality greater than
$C(\vec {\lambda })$
of cardinality greater than
![]() $\lambda $
that is definable by a
$\lambda $
that is definable by a
![]() $\Sigma _1$
-formula with parameter z.
$\Sigma _1$
-formula with parameter z.
Assume, towards a contradiction, that there is a perfect embedding
![]() ${\iota }:{{}^\omega \lambda }\longrightarrow {C(\vec {\lambda })}$
with
${\iota }:{{}^\omega \lambda }\longrightarrow {C(\vec {\lambda })}$
with
![]() ${\mathrm {{ran}}(\iota )}\subseteq X$
. Set
${\mathrm {{ran}}(\iota )}\subseteq X$
. Set
![]() $Y=\{{b_\gamma }~\vert ~{\lambda \leq \gamma <\lambda ^+}\}$
and let
$Y=\{{b_\gamma }~\vert ~{\lambda \leq \gamma <\lambda ^+}\}$
and let
![]() ${\zeta }:{X}\longrightarrow {Y}$
denote the unique map with
${\zeta }:{X}\longrightarrow {Y}$
denote the unique map with
![]() $\zeta (b)(n)=b(n+1)$
for all
$\zeta (b)(n)=b(n+1)$
for all
![]() $b\in X$
and
$b\in X$
and
![]() $n<\omega $
. Then
$n<\omega $
. Then
![]() $\zeta $
is a homeomorphism of the subspace X of
$\zeta $
is a homeomorphism of the subspace X of
![]() $C(\vec {\lambda })$
and the subspace Y of
$C(\vec {\lambda })$
and the subspace Y of
![]() $C(\vec {\lambda })$
. In particular, it follows that
$C(\vec {\lambda })$
. In particular, it follows that
![]() $\zeta \circ \iota $
is a perfect embedding of
$\zeta \circ \iota $
is a perfect embedding of
![]() ${}^\omega \lambda $
into
${}^\omega \lambda $
into
![]() $C(\vec {\lambda })$
with
$C(\vec {\lambda })$
with
![]() ${\mathrm {{ran}}(\zeta \circ \iota )}\subseteq Y\subseteq \mathsf {WO}(\vec {\lambda },\vec {a})$
. In this situation, Lemma 2.2 yields
${\mathrm {{ran}}(\zeta \circ \iota )}\subseteq Y\subseteq \mathsf {WO}(\vec {\lambda },\vec {a})$
. In this situation, Lemma 2.2 yields
![]() $c,d\in {}^\omega \lambda $
with
$c,d\in {}^\omega \lambda $
with
![]() $c\neq d$
and
$c\neq d$
and
![]() $\|(\zeta \circ \iota )(c)\|_{\vec {a}}=\|(\zeta \circ \iota )(d)\|_{\vec {a}}$
. By the definition of Y, this is a contradiction.
$\|(\zeta \circ \iota )(c)\|_{\vec {a}}=\|(\zeta \circ \iota )(d)\|_{\vec {a}}$
. By the definition of Y, this is a contradiction.
Note that, in order to construct an inner model N with
![]() $V_\lambda \subseteq N$
and the property that (ii) of the above theorem holds, it suffices to assume that
$V_\lambda \subseteq N$
and the property that (ii) of the above theorem holds, it suffices to assume that
![]() $\lambda $
is the supremum of
$\lambda $
is the supremum of
![]() $\omega $
-many inaccessible cardinals in order to carry out the construction made in the proof of the theorem.
$\omega $
-many inaccessible cardinals in order to carry out the construction made in the proof of the theorem.
In the remainder of this section, we further develop the arguments used in the above proof to obtain the following strengthening of Theorem 1.3.
Theorem 2.4. If
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
is a strictly increasing sequence of measurable cardinals with limit
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
is a strictly increasing sequence of measurable cardinals with limit
![]() $\lambda $
, then the following statements hold in an inner model M containing
$\lambda $
, then the following statements hold in an inner model M containing
![]() $\vec {\lambda }$
:
$\vec {\lambda }$
:
-
(i) The sequence
 $\vec {\lambda }$
consists of measurable cardinals.
$\vec {\lambda }$
consists of measurable cardinals. -
(ii) If
 $\vec {\nu }$
is a strictly increasing
$\vec {\nu }$
is a strictly increasing
 $\omega $
-sequence of cardinals of uncountable cofinality with limit
$\omega $
-sequence of cardinals of uncountable cofinality with limit
 $\lambda $
, then for some
$\lambda $
, then for some
 $x\in {H}_{{\aleph _1}}$
, there is a subset of
$x\in {H}_{{\aleph _1}}$
, there is a subset of
 $C(\vec {\lambda })$
of cardinality greater than
$C(\vec {\lambda })$
of cardinality greater than
 $\lambda $
that does not contain the range of a perfect embedding of
$\lambda $
that does not contain the range of a perfect embedding of
 ${}^\omega \lambda $
into
${}^\omega \lambda $
into
 $C(\vec {\lambda })$
and is definable by a
$C(\vec {\lambda })$
and is definable by a
 $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
 $\vec {\nu }$
and x.
$\vec {\nu }$
and x.
Proof. Pick a sequence
![]() $\langle {U_n}~\vert ~{n<\omega }\rangle $
with the property that
$\langle {U_n}~\vert ~{n<\omega }\rangle $
with the property that
![]() $U_n$
is a normal ultrafilter on
$U_n$
is a normal ultrafilter on
![]() $\lambda _n$
for all
$\lambda _n$
for all
![]() $n<\omega $
and define
$n<\omega $
and define
Then
![]() $\vec {\lambda }\in L[\mathcal {U}]$
and for every
$\vec {\lambda }\in L[\mathcal {U}]$
and for every
![]() $n<\omega $
, the cardinal
$n<\omega $
, the cardinal
![]() $\lambda _n$
is measurable in
$\lambda _n$
is measurable in
![]() $L[\mathcal {U}]$
.
$L[\mathcal {U}]$
.
Now, work in
![]() $L[\mathcal {U}]$
and fix a strictly increasing sequence
$L[\mathcal {U}]$
and fix a strictly increasing sequence
![]() $\vec {\nu }=\langle {\nu _n}~\vert ~{n<\omega }\rangle $
of cardinals of uncountable cofinality with limit
$\vec {\nu }=\langle {\nu _n}~\vert ~{n<\omega }\rangle $
of cardinals of uncountable cofinality with limit
![]() $\lambda $
. Using standard arguments about iterated measurable ultrapowers (see [Reference Kanamori9, Lemma 19.5] and [Reference Steel17, Section 3]), we can find
$\lambda $
. Using standard arguments about iterated measurable ultrapowers (see [Reference Kanamori9, Lemma 19.5] and [Reference Steel17, Section 3]), we can find
-
• a transitive class M,
-
• an elementary embedding
 ${j}:{V}\longrightarrow {M}$
with
${j}:{V}\longrightarrow {M}$
with
 $j(\lambda )=\lambda $
,
$j(\lambda )=\lambda $
, -
• a function
 ${x}:{\omega }\longrightarrow {\omega }$
, and
${x}:{\omega }\longrightarrow {\omega }$
, and -
• a sequence
 $\langle {C_n}~\vert ~{n<\omega }\rangle $
$\langle {C_n}~\vert ~{n<\omega }\rangle $
such that the following statements hold for all
![]() $n<\omega $
:
$n<\omega $
:
-
(i)
 $j(\lambda _n)=\nu _{x(n)}$
.
$j(\lambda _n)=\nu _{x(n)}$
. -
(ii)
 $\nu _{x(n+1)}>\vert {{H}_{{\nu _{x(n)}^+}}}\vert $
.
$\nu _{x(n+1)}>\vert {{H}_{{\nu _{x(n)}^+}}}\vert $
. -
(iii)
 $C_n$
is a closed unbounded subset of
$C_n$
is a closed unbounded subset of
 $\nu _{x(n)}$
.
$\nu _{x(n)}$
. -
(iv)
 $j(U_n)=\{{A\in M\cap {\mathcal {P}}({\nu _{x(n)}})}~\vert ~{\exists \xi <\nu _{x(n)}\ C_n\setminus \xi \subseteq A}\}$
.
$j(U_n)=\{{A\in M\cap {\mathcal {P}}({\nu _{x(n)}})}~\vert ~{\exists \xi <\nu _{x(n)}\ C_n\setminus \xi \subseteq A}\}$
.
Now, set
![]() $\mathcal {V}=j(\mathcal {U})$
and define
$\mathcal {V}=j(\mathcal {U})$
and define
![]() $\mathcal {N}$
to be the class of all pairs
$\mathcal {N}$
to be the class of all pairs
![]() $\langle N,\vec {F}\rangle $
with the property that N is a transitive set of cardinality
$\langle N,\vec {F}\rangle $
with the property that N is a transitive set of cardinality
![]() $\lambda $
,
$\lambda $
,
![]() $\vec {F}=\langle {F_n}~\vert ~{n<\omega }\rangle $
is a sequence of length
$\vec {F}=\langle {F_n}~\vert ~{n<\omega }\rangle $
is a sequence of length
![]() $\omega $
and there exists a sequence
$\omega $
and there exists a sequence
![]() $\langle {D_n}~\vert ~{n<\omega }\rangle $
such that the following statements hold:
$\langle {D_n}~\vert ~{n<\omega }\rangle $
such that the following statements hold:
-
(a)
 $D_n$
is a closed unbounded subset of
$D_n$
is a closed unbounded subset of
 $\nu _{x(n)}$
for all
$\nu _{x(n)}$
for all
 $n<\omega $
.
$n<\omega $
. -
(b) If
 $n<\omega $
, then
$n<\omega $
, then
 $F_n$
is an element of N,
$F_n$
is an element of N,
 $\nu _{x(n)}$
is a regular cardinal in N and
$\nu _{x(n)}$
is a regular cardinal in N and
 $F_n$
is a normal ultrafilter on
$F_n$
is a normal ultrafilter on
 $\nu _{x(n)}$
in N.
$\nu _{x(n)}$
in N. -
(c) If
 $n<\omega $
, then
$n<\omega $
, then
 $F_n=\{{A\in N\cap {\mathcal {P}}({\nu _{x(n)}})}~\vert ~{\exists \xi <\nu _{x(n)}\ D_n\setminus \xi \subseteq A}\}$
.
$F_n=\{{A\in N\cap {\mathcal {P}}({\nu _{x(n)}})}~\vert ~{\exists \xi <\nu _{x(n)}\ D_n\setminus \xi \subseteq A}\}$
. -
(d) If
 $\mathcal {F} = \{{\langle n,A\rangle }~\vert ~{n<\omega , ~ A\in F_n}\}$
, then
$\mathcal {F} = \{{\langle n,A\rangle }~\vert ~{n<\omega , ~ A\in F_n}\}$
, then
 $\mathcal {F}\in N$
and
$\mathcal {F}\in N$
and
 $N=L_{N\cap \mathrm {{Ord}}}[\mathcal {F}]$
.
$N=L_{N\cap \mathrm {{Ord}}}[\mathcal {F}]$
.
It is easy to see that the class
![]() $\mathcal {N}$
is definable by a
$\mathcal {N}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\vec {\nu }$
and x. Moreover, our assumptions ensure that for every
$\vec {\nu }$
and x. Moreover, our assumptions ensure that for every
![]() $x\in M\cap {\mathcal {P}}({\lambda })$
, there exists
$x\in M\cap {\mathcal {P}}({\lambda })$
, there exists
![]() $\gamma <\lambda ^+$
with
$\gamma <\lambda ^+$
with
![]() $x\in L_\gamma [\mathcal {V}]$
and
$x\in L_\gamma [\mathcal {V}]$
and
![]() $\langle L_\gamma [\mathcal {V}],\langle {j(U_n)}~\vert ~{n<\omega }\rangle \rangle \in \mathcal {N}$
.
$\langle L_\gamma [\mathcal {V}],\langle {j(U_n)}~\vert ~{n<\omega }\rangle \rangle \in \mathcal {N}$
.
Claim. If
![]() $\langle N,\langle {F_n}~\vert ~{n<\omega }\rangle \rangle \in \mathcal {N}$
and
$\langle N,\langle {F_n}~\vert ~{n<\omega }\rangle \rangle \in \mathcal {N}$
and
![]() $\mathcal {F} = \{{\langle n,A\rangle }~\vert ~{n<\omega , ~ A\in F_n}\}$
, then we have
$\mathcal {F} = \{{\langle n,A\rangle }~\vert ~{n<\omega , ~ A\in F_n}\}$
, then we have
![]() $\mathcal {F}\cap N=\mathcal {V}\cap L_{N\cap \mathrm {{Ord}}}[\mathcal {V}]$
and
$\mathcal {F}\cap N=\mathcal {V}\cap L_{N\cap \mathrm {{Ord}}}[\mathcal {V}]$
and
![]() $N=L_{N\cap \mathrm {{Ord}}}[\mathcal {V}]$
.
$N=L_{N\cap \mathrm {{Ord}}}[\mathcal {V}]$
.
Proof of the Claim.
Let
![]() $\langle {D_n}~\vert ~{n<\omega }\rangle $
be a sequence that witnesses that
$\langle {D_n}~\vert ~{n<\omega }\rangle $
be a sequence that witnesses that
![]() $\langle N,\langle {F_n}~\vert ~{n<\omega }\rangle \rangle $
is contained in
$\langle N,\langle {F_n}~\vert ~{n<\omega }\rangle \rangle $
is contained in
![]() $\mathcal {N}$
. Set
$\mathcal {N}$
. Set
![]() $\gamma =N\cap \mathrm {{Ord}}$
. By induction, we now show that
$\gamma =N\cap \mathrm {{Ord}}$
. By induction, we now show that
holds for all
![]() $\beta \leq \gamma $
. Hence, assume that
$\beta \leq \gamma $
. Hence, assume that
![]() $\beta \leq \gamma $
with
$\beta \leq \gamma $
with
![]() $\mathcal {F}\cap L_\alpha [\mathcal {F}]=\mathcal {V}\cap L_\alpha [\mathcal {V}]$
for all
$\mathcal {F}\cap L_\alpha [\mathcal {F}]=\mathcal {V}\cap L_\alpha [\mathcal {V}]$
for all
![]() $\alpha <\beta $
. Then
$\alpha <\beta $
. Then
![]() $L_\beta [\mathcal {F}]=L_\beta [\mathcal {V}]$
. Pick
$L_\beta [\mathcal {F}]=L_\beta [\mathcal {V}]$
. Pick
![]() $n<\omega $
and
$n<\omega $
and
![]() $A\in F_n$
with
$A\in F_n$
with
![]() $\langle n,A\rangle \in L_\beta [\mathcal {F}]$
. Then there exists
$\langle n,A\rangle \in L_\beta [\mathcal {F}]$
. Then there exists
![]() $\xi <\nu _{x(n)}$
with
$\xi <\nu _{x(n)}$
with
![]() $D_n\setminus \xi \subseteq A$
. Since
$D_n\setminus \xi \subseteq A$
. Since
![]() $C_n\cap D_n$
is unbounded in
$C_n\cap D_n$
is unbounded in
![]() $\nu _{x(n)}$
, we know that
$\nu _{x(n)}$
, we know that
![]() $A\cap C_n$
is unbounded in
$A\cap C_n$
is unbounded in
![]() $\nu _{x(n)}$
and hence there is no
$\nu _{x(n)}$
and hence there is no
![]() $\zeta <\nu _{x(n)}$
with the property that
$\zeta <\nu _{x(n)}$
with the property that
![]() $C_n\setminus \zeta \subseteq \nu _{x(n)}\setminus A$
. In this situation, the fact that
$C_n\setminus \zeta \subseteq \nu _{x(n)}\setminus A$
. In this situation, the fact that
![]() $j(U_n)$
is an ultrafilter on
$j(U_n)$
is an ultrafilter on
![]() $\nu _{x(n)}$
in
$\nu _{x(n)}$
in
![]() $L[\mathcal {V}]$
implies that
$L[\mathcal {V}]$
implies that
![]() $A\in j(U_n)$
and hence
$A\in j(U_n)$
and hence
![]() $\langle n,A\rangle \in j(\mathcal {U})\cap L_\beta [\mathcal {V}]=\mathcal {V}\cap L_\beta [\mathcal {V}]$
. The dual argument then shows that we also have
$\langle n,A\rangle \in j(\mathcal {U})\cap L_\beta [\mathcal {V}]=\mathcal {V}\cap L_\beta [\mathcal {V}]$
. The dual argument then shows that we also have
![]() $\mathcal {V}\cap L_\beta [\mathcal {V}]\subseteq \mathcal {F}\cap L_\beta [\mathcal {F}]$
. This completes the induction and we know that
$\mathcal {V}\cap L_\beta [\mathcal {V}]\subseteq \mathcal {F}\cap L_\beta [\mathcal {F}]$
. This completes the induction and we know that
![]() $\mathcal {F}\cap N=\mathcal {V}\cap L_\gamma [\mathcal {V}]$
. This allows us to conclude that
$\mathcal {F}\cap N=\mathcal {V}\cap L_\gamma [\mathcal {V}]$
. This allows us to conclude that
completing the proof of the claim.
Now, note that (ii) above ensures that there is a sequence
![]() $\langle {a_\alpha }~\vert ~{\alpha <\lambda }\rangle $
in M with the property that
$\langle {a_\alpha }~\vert ~{\alpha <\lambda }\rangle $
in M with the property that
holds for all
![]() $n<\omega $
. Define
$n<\omega $
. Define
![]() $\vec {a}$
to be the
$\vec {a}$
to be the
![]() $<_{L[\mathcal {V}]}$
-least sequence in M with this property.
$<_{L[\mathcal {V}]}$
-least sequence in M with this property.
Claim. The set
![]() $\{\vec {a}\}$
is definable by a
$\{\vec {a}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\vec {\nu }$
and x.
$\vec {\nu }$
and x.
Proof of the Claim.
First, note that our previous claim implies that, if
![]() $\langle N,\langle {F_n}~\vert ~{n<\omega }\rangle \rangle $
is an element of
$\langle N,\langle {F_n}~\vert ~{n<\omega }\rangle \rangle $
is an element of
![]() $\mathcal {N}$
with
$\mathcal {N}$
with
![]() $\lambda \in N$
, then
$\lambda \in N$
, then
![]() $N=L_{N\cap \mathrm {{Ord}}}[\mathcal {V}]$
and N contains all bounded subsets of
$N=L_{N\cap \mathrm {{Ord}}}[\mathcal {V}]$
and N contains all bounded subsets of
![]() $\lambda $
in M. It follows that
$\lambda $
in M. It follows that
![]() $\vec {a}$
is the unique sequence of length
$\vec {a}$
is the unique sequence of length
![]() $\lambda $
with the property that there exists
$\lambda $
with the property that there exists
![]() $\langle N, \langle {F_n}~\vert ~{n < \omega }\rangle \rangle $
in
$\langle N, \langle {F_n}~\vert ~{n < \omega }\rangle \rangle $
in
![]() $\mathcal {N}$
and
$\mathcal {N}$
and
![]() $\mathcal {F} = \{{\langle n, A\rangle }~\vert ~{n < \omega , A \in F_n}\}$
such that
$\mathcal {F} = \{{\langle n, A\rangle }~\vert ~{n < \omega , A \in F_n}\}$
such that
![]() $\vec {a}$
is the
$\vec {a}$
is the
![]() $<_{L[\mathcal {F}]}$
-least element of N with (1) for all
$<_{L[\mathcal {F}]}$
-least element of N with (1) for all
![]() $n<\omega $
. This characterization directly yields the desired
$n<\omega $
. This characterization directly yields the desired
![]() $\Sigma _1$
-definition.
$\Sigma _1$
-definition.
Next, notice that, if y is an element of
![]() $\mathcal {W}\mathcal {O}_\lambda ^M$
, then M contains an order-isomorphism between
$\mathcal {W}\mathcal {O}_\lambda ^M$
, then M contains an order-isomorphism between
![]() $\langle \lambda ,\lhd _y\rangle $
and
$\langle \lambda ,\lhd _y\rangle $
and
![]() $\langle \gamma ,<\rangle $
for some ordinal
$\langle \gamma ,<\rangle $
for some ordinal
![]() $\gamma \in [\lambda ,\lambda ^+)$
and this isomorphism witnesses that x is an element of
$\gamma \in [\lambda ,\lambda ^+)$
and this isomorphism witnesses that x is an element of
![]() $\mathcal {W}\mathcal {O}_\lambda $
in V. This shows that
$\mathcal {W}\mathcal {O}_\lambda $
in V. This shows that
![]() $\mathcal {W}\mathcal {O}_\lambda ^M\subseteq \mathcal {W}\mathcal {O}_\lambda $
,
$\mathcal {W}\mathcal {O}_\lambda ^M\subseteq \mathcal {W}\mathcal {O}_\lambda $
,
![]() $\mathsf {WO}(\vec {\nu },\vec {a})^M\subseteq \mathsf {WO}(\vec {\nu },\vec {a})$
and
$\mathsf {WO}(\vec {\nu },\vec {a})^M\subseteq \mathsf {WO}(\vec {\nu },\vec {a})$
and
![]() $\|b\|_{\vec {a}}=\|b\|_{\vec {a}}^M$
for all
$\|b\|_{\vec {a}}=\|b\|_{\vec {a}}^M$
for all
![]() $b\in \mathsf {WO}(\vec {\nu },\vec {a})^M$
. Moreover, using (1) and the fact that
$b\in \mathsf {WO}(\vec {\nu },\vec {a})^M$
. Moreover, using (1) and the fact that
![]() $\lambda ^+=(\lambda ^+)^M$
, we can pick a sequence
$\lambda ^+=(\lambda ^+)^M$
, we can pick a sequence
![]() $\langle {b_\gamma }~\vert ~{\lambda \leq \gamma <\lambda ^+}\rangle $
with the property that for all
$\langle {b_\gamma }~\vert ~{\lambda \leq \gamma <\lambda ^+}\rangle $
with the property that for all
![]() $\gamma <\lambda ^+$
, the set
$\gamma <\lambda ^+$
, the set
![]() $b_\gamma $
is the
$b_\gamma $
is the
![]() $<_{L[\mathcal {V}]}$
-least element of
$<_{L[\mathcal {V}]}$
-least element of
![]() $\mathsf {WO}(\vec {\nu },\vec {a})^M$
with the property that
$\mathsf {WO}(\vec {\nu },\vec {a})^M$
with the property that
![]() $\|b_\gamma \|_{\vec {a}}=\gamma $
and
$\|b_\gamma \|_{\vec {a}}=\gamma $
and
![]() $b_\gamma (x(n))<\nu _{x(n+1)}$
for all
$b_\gamma (x(n))<\nu _{x(n+1)}$
for all
![]() $n<\omega $
. The following statement now follows from a combination of the above claims:
$n<\omega $
. The following statement now follows from a combination of the above claims:
Claim. The set
![]() $B=\{{b_\gamma }~\vert ~{\lambda \leq \gamma <\lambda ^+}\}$
is definable by a
$B=\{{b_\gamma }~\vert ~{\lambda \leq \gamma <\lambda ^+}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\vec {\nu }$
and x.
$\vec {\nu }$
and x.
Given
![]() $\lambda \leq \gamma <\lambda ^+$
, we let
$\lambda \leq \gamma <\lambda ^+$
, we let
![]() $c_\gamma $
denote the unique element of
$c_\gamma $
denote the unique element of
![]() ${}^\omega \lambda $
such that the following statements hold for all
${}^\omega \lambda $
such that the following statements hold for all
![]() $n<\omega $
:
$n<\omega $
:
-
• If n is of the form
 $x(m+1)$
for some
$x(m+1)$
for some
 $m<\omega $
, then
$m<\omega $
, then
 $c_\gamma (n)=b_\gamma (x(m))$
.
$c_\gamma (n)=b_\gamma (x(m))$
. -
• If
 $n\neq x(m+1)$
for all
$n\neq x(m+1)$
for all
 $m<\omega $
, then
$m<\omega $
, then
 $c_\gamma (n)=0$
.
$c_\gamma (n)=0$
.
We then know that
![]() $c_\gamma \in C(\vec {\nu })$
for all
$c_\gamma \in C(\vec {\nu })$
for all
![]() $\lambda \leq \gamma <\lambda ^+$
.
$\lambda \leq \gamma <\lambda ^+$
.
Claim. The set
![]() $C=\{{c_\gamma }~\vert ~{\lambda \leq \gamma <\lambda ^+}\}$
has cardinality
$C=\{{c_\gamma }~\vert ~{\lambda \leq \gamma <\lambda ^+}\}$
has cardinality
![]() $\lambda ^+$
and is definable by a
$\lambda ^+$
and is definable by a
![]() $\Sigma _1$
-formula with parameters
$\Sigma _1$
-formula with parameters
![]() $\vec {\nu }$
and x.
$\vec {\nu }$
and x.
Let
![]() ${\zeta }:{B}\longrightarrow {C}$
denote the unique function with
${\zeta }:{B}\longrightarrow {C}$
denote the unique function with
![]() $\zeta (b_\gamma )=c_\gamma $
for all
$\zeta (b_\gamma )=c_\gamma $
for all
![]() $\lambda \leq \gamma <\lambda ^+$
.
$\lambda \leq \gamma <\lambda ^+$
.
Claim. The map
![]() $\zeta $
is a homeomorphism of the subspace B of
$\zeta $
is a homeomorphism of the subspace B of
![]() $C(\vec {\nu })$
and the subspace C of
$C(\vec {\nu })$
and the subspace C of
![]() $C(\vec {\nu })$
.
$C(\vec {\nu })$
.
Now, assume, towards a contradiction, that there is a perfect embedding
![]() ${\iota }:{{}^\omega \lambda }\longrightarrow {C(\vec {\nu })}$
with the property that
${\iota }:{{}^\omega \lambda }\longrightarrow {C(\vec {\nu })}$
with the property that
![]() ${\mathrm {{ran}}(\iota )}\subseteq C$
. Then
${\mathrm {{ran}}(\iota )}\subseteq C$
. Then
![]() $\zeta ^{{-}1}\circ \iota $
is a perfect embedding of
$\zeta ^{{-}1}\circ \iota $
is a perfect embedding of
![]() ${}^\omega \lambda $
into
${}^\omega \lambda $
into
![]() $C(\vec {\nu })$
and
$C(\vec {\nu })$
and
An application of Lemma 2.2 now yields
![]() $c,d\in {}^\omega \lambda $
with
$c,d\in {}^\omega \lambda $
with
![]() $c\neq d$
and
$c\neq d$
and
contradicting the definition of B.
3
 $\Sigma _1$
-definability at I2-cardinals
$\Sigma _1$
-definability at I2-cardinals
Let
![]() ${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and set
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and set
![]() $\lambda =\sup _{n<\omega }\lambda _n$
. Classical results (see [Reference Martin15]) then show that j is
$\lambda =\sup _{n<\omega }\lambda _n$
. Classical results (see [Reference Martin15]) then show that j is
![]() $\omega $
-iterable, i.e., there exists a commuting system
$\omega $
-iterable, i.e., there exists a commuting system
of inner models and elementary embeddings such that the following statements hold:
-
(i)
 $M^j_0=V$
and
$M^j_0=V$
and
 $j_{0,1}=j$
.
$j_{0,1}=j$
. -
(ii) If
 $n<\omega $
, then
$n<\omega $
, then
 $j_{n+1,n+2}=\bigcup \{{j_{n,n+1}(j_{n,n+1}\restriction V_\alpha )}~\vert ~{\alpha \in \mathrm {{Ord}}}\}$
.
$j_{n+1,n+2}=\bigcup \{{j_{n,n+1}(j_{n,n+1}\restriction V_\alpha )}~\vert ~{\alpha \in \mathrm {{Ord}}}\}$
. -
(iii)
 $\langle M^j_\omega ,\langle {j_{n,\omega }}~\vert ~{n<\omega }\rangle \rangle $
is a direct limit of
$\langle M^j_\omega ,\langle {j_{n,\omega }}~\vert ~{n<\omega }\rangle \rangle $
is a direct limit of  $$ \begin{align*}\langle\langle{M^j_n}~\vert~{n<\omega}\rangle,\langle{{j_{m,n}}:{M^j_m}\longrightarrow{M^j_n}}~\vert~{m\leq n<\omega}\rangle\rangle.\end{align*} $$
$$ \begin{align*}\langle\langle{M^j_n}~\vert~{n<\omega}\rangle,\langle{{j_{m,n}}:{M^j_m}\longrightarrow{M^j_n}}~\vert~{m\leq n<\omega}\rangle\rangle.\end{align*} $$
Given
![]() $m\leq n<\omega $
, we then have
$m\leq n<\omega $
, we then have
![]() $V_\lambda \subseteq M^j_\omega \subseteq M^j_n\subseteq M^j_m$
,
$V_\lambda \subseteq M^j_\omega \subseteq M^j_n\subseteq M^j_m$
,
![]() ${\mathrm {{crit}}({j_{n,{n+1}}})}=\lambda _n=j_{m,n}(\lambda _m)$
,
${\mathrm {{crit}}({j_{n,{n+1}}})}=\lambda _n=j_{m,n}(\lambda _m)$
,
![]() $j_{m,n}(\lambda )=\lambda $
and
$j_{m,n}(\lambda )=\lambda $
and
![]() $j_{n,\omega }(\lambda _n)=\lambda $
. Moreover, it is easy to see that
$j_{n,\omega }(\lambda _n)=\lambda $
. Moreover, it is easy to see that
![]() $j_{0,\omega }(\lambda ^+)=\lambda ^+$
holds and therefore
$j_{0,\omega }(\lambda ^+)=\lambda ^+$
holds and therefore
![]() $(2^\lambda )^{M^j_\omega }<\lambda ^+$
. Note that the Mathias criterion shows that the sequence
$(2^\lambda )^{M^j_\omega }<\lambda ^+$
. Note that the Mathias criterion shows that the sequence
![]() $\vec {\lambda }$
is Prikry-generic over
$\vec {\lambda }$
is Prikry-generic over
![]() $M^j_\omega $
and, by the theory of Prikry-type forcings, this implies that
$M^j_\omega $
and, by the theory of Prikry-type forcings, this implies that
![]() $(2^\lambda )^{M^j_\omega [\vec {\lambda }]}<\lambda ^+$
.
$(2^\lambda )^{M^j_\omega [\vec {\lambda }]}<\lambda ^+$
.
The following theorem is the main result of this section. We will later show that it is a direct strengthening of Theorem 1.4.
Theorem 3.1. Let
![]() ${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and let N be an inner model of
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and let N be an inner model of
![]() $\operatorname {\mathrm {ZFC}}$
with
$\operatorname {\mathrm {ZFC}}$
with
![]() $M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
. Set
$M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
. Set
![]() $\lambda =\sup _{n<\omega }\lambda _n$
. If X is a subset of
$\lambda =\sup _{n<\omega }\lambda _n$
. If X is a subset of
![]() $C(\vec {\lambda })$
with
$C(\vec {\lambda })$
with
![]() $\vert X\vert>(2^\lambda )^N$
that is definable over
$\vert X\vert>(2^\lambda )^N$
that is definable over
![]() $V_\lambda $
by a
$V_\lambda $
by a
![]() $\Sigma ^1_2$
-formula with parameters in
$\Sigma ^1_2$
-formula with parameters in
![]() $V_{\lambda +1}^N$
, then there is a perfect embedding
$V_{\lambda +1}^N$
, then there is a perfect embedding
![]() ${\iota }:{{}^\omega \lambda }\longrightarrow {C(\vec {\lambda })}$
with
${\iota }:{{}^\omega \lambda }\longrightarrow {C(\vec {\lambda })}$
with
![]() ${\mathrm {{ran}}(\iota )}\subseteq X$
.
${\mathrm {{ran}}(\iota )}\subseteq X$
.
The proof of the above theorem closely follows the proof of Solovay’s classical result showing that every
![]() $\mathbf {\Sigma }^1_2$
-set of reals has the perfect set property if
$\mathbf {\Sigma }^1_2$
-set of reals has the perfect set property if
![]() $\omega _1$
is inaccessible to the reals (see [Reference Kanamori9, Theorem 14.10]). The key ingredient that makes this adaptation possible is an absoluteness theorem proven by Laver in [Reference Laver11]. We start this argument by obtaining tree representations for the sets in the given definability class.
$\omega _1$
is inaccessible to the reals (see [Reference Kanamori9, Theorem 14.10]). The key ingredient that makes this adaptation possible is an absoluteness theorem proven by Laver in [Reference Laver11]. We start this argument by obtaining tree representations for the sets in the given definability class.
Given non-empty sets
![]() $a_0,\ldots ,a_k$
, a subset T of
$a_0,\ldots ,a_k$
, a subset T of
![]() ${}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_k$
is a (descriptive) tree if the following statements hold for all elements
${}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_k$
is a (descriptive) tree if the following statements hold for all elements
![]() $\langle t_0,\ldots ,t_k\rangle $
of T:
$\langle t_0,\ldots ,t_k\rangle $
of T:
-
•
 $\operatorname {\mathrm {dom}}(t_0)=\ldots =\operatorname {\mathrm {dom}}(t_k)$
.
$\operatorname {\mathrm {dom}}(t_0)=\ldots =\operatorname {\mathrm {dom}}(t_k)$
. -
• If
 $\ell \in \operatorname {\mathrm {dom}}(t_k)$
, then
$\ell \in \operatorname {\mathrm {dom}}(t_k)$
, then
 $\langle t_0\restriction \ell ,\ldots ,t_k\restriction \ell \rangle \in T$
.
$\langle t_0\restriction \ell ,\ldots ,t_k\restriction \ell \rangle \in T$
.
In addition, if
![]() $T\subseteq {}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_k$
is a tree, then we let
$T\subseteq {}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_k$
is a tree, then we let
![]() $[T]$
denote the set of all tuples
$[T]$
denote the set of all tuples
![]() $\langle x_0,\ldots ,x_k\rangle $
in
$\langle x_0,\ldots ,x_k\rangle $
in
![]() ${}^\omega a_0\times \ldots \times {}^\omega a_k$
with the property that
${}^\omega a_0\times \ldots \times {}^\omega a_k$
with the property that
![]() $\langle x_0\restriction \ell ,\ldots ,x_k\restriction \ell \rangle \in T$
holds for all
$\langle x_0\restriction \ell ,\ldots ,x_k\restriction \ell \rangle \in T$
holds for all
![]() $\ell <\omega $
. Finally, for every tree
$\ell <\omega $
. Finally, for every tree
![]() $T\subseteq {}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_{k+1}$
, we define
$T\subseteq {}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_{k+1}$
, we define
As outlined in [Reference Laver11, Section 1], for singular strong limit cardinals
![]() $\lambda $
and
$\lambda $
and
![]() $0<k<\omega $
, there is a direct correspondence between subsets of
$0<k<\omega $
, there is a direct correspondence between subsets of
![]() $V_{\lambda +1}^k$
that are
$V_{\lambda +1}^k$
that are
![]() $\mathbf {\Sigma }^1_1$
-definable over
$\mathbf {\Sigma }^1_1$
-definable over
![]() $V_\lambda $
and sets of the form
$V_\lambda $
and sets of the form
![]() $p[T]$
for trees
$p[T]$
for trees
![]() $T\subseteq ({}^{{<}\omega }V_\lambda )^{k+1}$
. Several key arguments in this section rely on the absoluteness properties of this correspondence that can be isolated from the arguments in [Reference Laver11, Section 1]:
$T\subseteq ({}^{{<}\omega }V_\lambda )^{k+1}$
. Several key arguments in this section rely on the absoluteness properties of this correspondence that can be isolated from the arguments in [Reference Laver11, Section 1]:
Lemma 3.2. For every
![]() $\Sigma _1^1$
-formula
$\Sigma _1^1$
-formula
![]() $\varphi (w_0,\ldots ,w_{k+2})$
in the language of set theory with free second-order variables
$\varphi (w_0,\ldots ,w_{k+2})$
in the language of set theory with free second-order variables
![]() $w_0,\ldots ,w_{k+2}$
, there is a first-order formula
$w_0,\ldots ,w_{k+2}$
, there is a first-order formula
![]() $\psi (v_0,\ldots ,v_{k+1})$
in the language of set theory expanded by two unary relation symbols with free variables
$\psi (v_0,\ldots ,v_{k+1})$
in the language of set theory expanded by two unary relation symbols with free variables
![]() $v_0,\ldots ,v_{k+1}$
such that
$v_0,\ldots ,v_{k+1}$
such that
![]() $\operatorname {\mathrm {ZFC}}$
proves that for every strictly increasing sequence
$\operatorname {\mathrm {ZFC}}$
proves that for every strictly increasing sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of strong limit cardinals with supremum
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of strong limit cardinals with supremum
![]() $\lambda $
and every
$\lambda $
and every
![]() $B\subseteq V_\lambda $
, the set
$B\subseteq V_\lambda $
, the set
is a tree and the following statements hold:
-
(i)
 $T_{\varphi ,B,\vec {\lambda }}\cap ({}^n V_\lambda )^{k+2}\in V_\lambda $
for all
$T_{\varphi ,B,\vec {\lambda }}\cap ({}^n V_\lambda )^{k+2}\in V_\lambda $
for all
 $n<\omega $
.
$n<\omega $
. -
(ii) If
 $\langle x_0,\ldots ,x_k\rangle \in p[T_{\varphi ,B,\vec {\lambda }}]$
,
$\langle x_0,\ldots ,x_k\rangle \in p[T_{\varphi ,B,\vec {\lambda }}]$
,
 $i\leq k$
and
$i\leq k$
and
 $m<n<\omega $
, then
$m<n<\omega $
, then
 $x_i(m)=x_i(n)\cap V_{\lambda _m}$
.
$x_i(m)=x_i(n)\cap V_{\lambda _m}$
. -
(iii) The following statements are equivalent for all
 $A_0,\ldots ,A_k\subseteq V_\lambda $
:
$A_0,\ldots ,A_k\subseteq V_\lambda $
:-
(a)
 $\langle V_\lambda ,\in \rangle \models \varphi (A_0,\ldots ,A_k,B,\vec {\lambda })$
.
$\langle V_\lambda ,\in \rangle \models \varphi (A_0,\ldots ,A_k,B,\vec {\lambda })$
. -
(b) There is
 $\langle x_0,\ldots ,x_k\rangle \in p[T_{\varphi ,B,\vec {\lambda }}]$
with
$\langle x_0,\ldots ,x_k\rangle \in p[T_{\varphi ,B,\vec {\lambda }}]$
with
 $x_i(n)=A_i\cap V_{\lambda _n}$
for all
$x_i(n)=A_i\cap V_{\lambda _n}$
for all
 $i\leq k$
and
$i\leq k$
and
 $n<\omega $
.
$n<\omega $
.
-
The above lemma provides a setting in which a converse of Proposition 1.6 holds.
Corollary 3.3. For every
![]() $\Sigma ^1_2$
-formula
$\Sigma ^1_2$
-formula
![]() $\psi (w_0,\ldots ,w_{k-1})$
in the language of set theory with free second-order parameters
$\psi (w_0,\ldots ,w_{k-1})$
in the language of set theory with free second-order parameters
![]() $w_0,\ldots ,w_{k-1}$
, there exists a
$w_0,\ldots ,w_{k-1}$
, there exists a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\varphi (v_0,\ldots ,v_k)$
in the language of set theory such that
$\varphi (v_0,\ldots ,v_k)$
in the language of set theory such that
![]() $\operatorname {\mathrm {ZFC}}$
proves that
$\operatorname {\mathrm {ZFC}}$
proves that
holds for every strictly increasing sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of strong limit cardinals with supremum
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of strong limit cardinals with supremum
![]() $\lambda $
and all
$\lambda $
and all
![]() $A_0,\ldots ,A_{k-1}\in V_{\lambda +1}$
.
$A_0,\ldots ,A_{k-1}\in V_{\lambda +1}$
.
Following [Reference Laver11, Section 1], we now generalize the concept of Shoenfield trees (i.e., tree representations for
![]() $\mathbf {\Sigma }^1_2$
-sets of real numbers) to higher cardinals of countable cofinality. Given a tree
$\mathbf {\Sigma }^1_2$
-sets of real numbers) to higher cardinals of countable cofinality. Given a tree
![]() $T\subseteq {}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_k$
,
$T\subseteq {}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_k$
,
![]() $i<k$
and
$i<k$
and
![]() $\langle s_0,\ldots ,s_i\rangle \in {}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_i$
with
$\langle s_0,\ldots ,s_i\rangle \in {}^{{<}\omega }a_0\times \ldots \times {}^{{<}\omega }a_i$
with
![]() $\operatorname {\mathrm {dom}}(s_0)=\ldots =\operatorname {\mathrm {dom}}(s_i)$
, we define
$\operatorname {\mathrm {dom}}(s_0)=\ldots =\operatorname {\mathrm {dom}}(s_i)$
, we define
![]() $T^{\langle s_0,\ldots ,s_i\rangle }$
to be the set of all tuples
$T^{\langle s_0,\ldots ,s_i\rangle }$
to be the set of all tuples
![]() $\langle t_{i+1},\ldots ,t_k\rangle $
in
$\langle t_{i+1},\ldots ,t_k\rangle $
in
![]() ${}^{{<}\omega }a_{i+1}\times \ldots \times {}^{{<}\omega }a_k$
with the property that
${}^{{<}\omega }a_{i+1}\times \ldots \times {}^{{<}\omega }a_k$
with the property that
and
Note that
holds for all
![]() $\ell \in \operatorname {\mathrm {dom}}(s_0)$
. In addition, for every ordinal
$\ell \in \operatorname {\mathrm {dom}}(s_0)$
. In addition, for every ordinal
![]() $\theta $
, we let
$\theta $
, we let
![]() $R_{T,\theta }(s_0,\ldots ,s_i)$
denote the set of functions
$R_{T,\theta }(s_0,\ldots ,s_i)$
denote the set of functions
satisfying
for all
![]() $\langle t_{i+1},\ldots ,t_k\rangle \in T^{\langle s_0,\ldots ,s_i\rangle }$
and
$\langle t_{i+1},\ldots ,t_k\rangle \in T^{\langle s_0,\ldots ,s_i\rangle }$
and
![]() $\ell <\operatorname {\mathrm {dom}}(t_k)$
. It is then easy to see that
$\ell <\operatorname {\mathrm {dom}}(t_k)$
. It is then easy to see that
![]() $r\restriction T^{\langle s_0\restriction \ell ,\ldots ,s_i\restriction \ell \rangle }$
is an element of
$r\restriction T^{\langle s_0\restriction \ell ,\ldots ,s_i\restriction \ell \rangle }$
is an element of
![]() $R_{T,\theta }(s_0\restriction \ell ,\ldots ,s_i\restriction \ell )$
for all
$R_{T,\theta }(s_0\restriction \ell ,\ldots ,s_i\restriction \ell )$
for all
![]() $r\in R_{T,\theta }(s_0,\ldots ,s_i)$
and
$r\in R_{T,\theta }(s_0,\ldots ,s_i)$
and
![]() $\ell <\operatorname {\mathrm {dom}}(s_0)$
.
$\ell <\operatorname {\mathrm {dom}}(s_0)$
.
Now, let
![]() $\lambda $
be an infinite ordinal, let
$\lambda $
be an infinite ordinal, let
![]() $T\subseteq ({}^{{<}\omega }V_\lambda )^{k+3}$
be a tree and let
$T\subseteq ({}^{{<}\omega }V_\lambda )^{k+3}$
be a tree and let
![]() $\theta>\lambda $
be an ordinal. We then define
$\theta>\lambda $
be an ordinal. We then define
![]() $S_{T,\theta }$
to be the subset of
$S_{T,\theta }$
to be the subset of
![]() $({}^{{<}\omega }V_{\theta +\omega })^{k+2}$
consisting of all tuples
$({}^{{<}\omega }V_{\theta +\omega })^{k+2}$
consisting of all tuples
![]() $\langle s_0,\ldots ,s_k,t\rangle $
such that the following statements hold:
$\langle s_0,\ldots ,s_k,t\rangle $
such that the following statements hold:
-
•
 $s_0,\ldots ,s_k\in {}^{{<}\omega }V_\lambda $
.
$s_0,\ldots ,s_k\in {}^{{<}\omega }V_\lambda $
. -
•
 $\operatorname {\mathrm {dom}}(s_0)=\ldots =\operatorname {\mathrm {dom}}(s_k)=\operatorname {\mathrm {dom}}(t)$
.
$\operatorname {\mathrm {dom}}(s_0)=\ldots =\operatorname {\mathrm {dom}}(s_k)=\operatorname {\mathrm {dom}}(t)$
. -
• There exists
 $s_{k+1}\in {}^{\operatorname {\mathrm {dom}}(s_0)}V_\lambda $
and
$s_{k+1}\in {}^{\operatorname {\mathrm {dom}}(s_0)}V_\lambda $
and
 $r\in R_{T,\theta }(s_0,\ldots ,s_{k+1})$
such that (3)holds for all
$r\in R_{T,\theta }(s_0,\ldots ,s_{k+1})$
such that (3)holds for all $$ \begin{align} t(\ell) ~ = ~ \langle s_{k+1}\restriction(\ell+1), ~ r\restriction T^{\langle s_0\restriction(\ell+1),\ldots,s_{k+1}\restriction(\ell+1)}\rangle \end{align} $$
$$ \begin{align} t(\ell) ~ = ~ \langle s_{k+1}\restriction(\ell+1), ~ r\restriction T^{\langle s_0\restriction(\ell+1),\ldots,s_{k+1}\restriction(\ell+1)}\rangle \end{align} $$
 $\ell \in \operatorname {\mathrm {dom}}(t)$
.
$\ell \in \operatorname {\mathrm {dom}}(t)$
.
It is then easy to check that
![]() $S_{T,\theta }$
is a tree. The following lemma from [Reference Laver11, Section 1] shows how these constructions yield tree representations of
$S_{T,\theta }$
is a tree. The following lemma from [Reference Laver11, Section 1] shows how these constructions yield tree representations of
![]() $\mathbf {\Sigma }^1_2$
-subsets of
$\mathbf {\Sigma }^1_2$
-subsets of
![]() $V_{\lambda +1}$
:
$V_{\lambda +1}$
:
Lemma 3.4. Let
![]() $\varphi (w_0,\ldots ,w_{k+3})$
be a
$\varphi (w_0,\ldots ,w_{k+3})$
be a
![]() $\Sigma _1^1$
-formula in the language of set theory with free second-order variables
$\Sigma _1^1$
-formula in the language of set theory with free second-order variables
![]() $w_0,\ldots ,w_{k+3}$
. Then the following statements are equivalent for every strictly increasing sequence of inaccessible cardinals
$w_0,\ldots ,w_{k+3}$
. Then the following statements are equivalent for every strictly increasing sequence of inaccessible cardinals
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
with supremum
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
with supremum
![]() $\lambda $
, every limit ordinal
$\lambda $
, every limit ordinal
![]() $\theta \geq \lambda ^+$
and all
$\theta \geq \lambda ^+$
and all
![]() $A_0,\ldots ,A_k,B\subseteq V_\lambda $
:
$A_0,\ldots ,A_k,B\subseteq V_\lambda $
:
-
(i)
 $\langle V_\lambda ,\in \rangle \models \exists C ~ \neg \varphi (A_0,\ldots ,A_k,B,C,\vec {\lambda })$
.
$\langle V_\lambda ,\in \rangle \models \exists C ~ \neg \varphi (A_0,\ldots ,A_k,B,C,\vec {\lambda })$
. -
(ii) There is
 $\langle x_0,\ldots ,x_k\rangle \in p[S_{T_{\varphi ,B,\vec {\lambda }},\theta }]$
with
$\langle x_0,\ldots ,x_k\rangle \in p[S_{T_{\varphi ,B,\vec {\lambda }},\theta }]$
with
 $x_i(n)=A_i\cap V_{\lambda _n}$
for all
$x_i(n)=A_i\cap V_{\lambda _n}$
for all
 $i\leq k$
and
$i\leq k$
and
 $n<\omega $
.
$n<\omega $
.
Still following Laver’s arguments, we now show that the structural properties of higher Shoenfield trees can be fruitfully combined with the combinatorics of I2-embeddings. The proof of the next lemma is a reformulation of the proof of [Reference Laver11, Theorem 1.4].
Lemma 3.5. Let
![]() $\varphi (w_0,\ldots ,w_{k+3})$
be a
$\varphi (w_0,\ldots ,w_{k+3})$
be a
![]() $\Sigma _1^1$
-formula in the language of set theory with free second-order variables
$\Sigma _1^1$
-formula in the language of set theory with free second-order variables
![]() $w_0,\ldots ,w_{k+3}$
, let
$w_0,\ldots ,w_{k+3}$
, let
![]() ${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and let N be an inner model of
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and let N be an inner model of
![]() $\operatorname {\mathrm {ZFC}}$
with
$\operatorname {\mathrm {ZFC}}$
with
![]() $M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
. Set
$M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
. Set
![]() $\lambda =\sup _{n<\omega }\lambda _n$
and
$\lambda =\sup _{n<\omega }\lambda _n$
and
![]() $\theta =(\lambda ^+)^V$
. Fix
$\theta =(\lambda ^+)^V$
. Fix
![]() $B\in V_{\lambda +1}^N$
and define
$B\in V_{\lambda +1}^N$
and define
![]() $T=T_{\varphi ,B,\vec {\lambda }}^V$
. Then the following statements hold:
$T=T_{\varphi ,B,\vec {\lambda }}^V$
. Then the following statements hold:
-
(i)
 $T=T_{\varphi ,B,\vec {\lambda }}^N$
and
$T=T_{\varphi ,B,\vec {\lambda }}^N$
and
 $S_{T,\theta }^N\subseteq S_{T,\theta }^V$
.
$S_{T,\theta }^N\subseteq S_{T,\theta }^V$
. -
(ii) There is an inclusion-preserving embedding
 ${\Lambda }:{S_{T,\theta }^V}\longrightarrow {S_{T,\theta }^N}$
with the property that for all
${\Lambda }:{S_{T,\theta }^V}\longrightarrow {S_{T,\theta }^N}$
with the property that for all
 $\langle s_0,\ldots ,s_k,t\rangle \in S_{T,\theta }^V$
, there exists u with
$\langle s_0,\ldots ,s_k,t\rangle \in S_{T,\theta }^V$
, there exists u with  $$ \begin{align*}\Lambda(\langle s_0,\ldots,s_k,t\rangle) ~ = ~ \langle s_0,\ldots,s_k,u\rangle.\end{align*} $$
$$ \begin{align*}\Lambda(\langle s_0,\ldots,s_k,t\rangle) ~ = ~ \langle s_0,\ldots,s_k,u\rangle.\end{align*} $$
-
(iii)
 $p[S_{T,\theta }^V]^V=p[S_{T,\theta }^N]^V$
.
$p[S_{T,\theta }^V]^V=p[S_{T,\theta }^N]^V$
. -
(iv)
 $p[S_{T,\theta }^V]^V\cap N=p[S_{T,\theta }^N]^N$
.
$p[S_{T,\theta }^V]^V\cap N=p[S_{T,\theta }^N]^N$
.
Proof. (i) Since
![]() $V_\lambda \cup \{B,\vec {\lambda }\}\subseteq N$
, the fact that (2) holds in both V and N directly implies that
$V_\lambda \cup \{B,\vec {\lambda }\}\subseteq N$
, the fact that (2) holds in both V and N directly implies that
![]() $T=T_{\varphi ,B,\vec {\lambda }}^N$
. In addition, if
$T=T_{\varphi ,B,\vec {\lambda }}^N$
. In addition, if
![]() $s_0,\ldots ,s_{k+1}\in {}^{{<}\omega }V_\lambda $
with
$s_0,\ldots ,s_{k+1}\in {}^{{<}\omega }V_\lambda $
with
![]() $\operatorname {\mathrm {dom}}(s_0)=\ldots =\operatorname {\mathrm {dom}}(s_{k+1})$
, then
$\operatorname {\mathrm {dom}}(s_0)=\ldots =\operatorname {\mathrm {dom}}(s_{k+1})$
, then
In particular, we know that
![]() $S_{T,\theta }^N\subseteq S_{T,\theta }^V$
.
$S_{T,\theta }^N\subseteq S_{T,\theta }^V$
.
(ii) The proof of [Reference Laver11, Theorem 1.4] shows that for every
![]() $d\in V_\lambda $
and every function
$d\in V_\lambda $
and every function
![]() ${f}:{d}\longrightarrow {\mathrm {{Ord}}}$
, the function
${f}:{d}\longrightarrow {\mathrm {{Ord}}}$
, the function
![]() ${j_{0,\omega }\circ f}:{d}\longrightarrow {\mathrm {{Ord}}}$
is an element of
${j_{0,\omega }\circ f}:{d}\longrightarrow {\mathrm {{Ord}}}$
is an element of
![]() $M^j_\omega $
. In particular, if
$M^j_\omega $
. In particular, if
![]() $s_0,\ldots ,s_{k+1}\in {}^{{<}\omega }V_\lambda $
with
$s_0,\ldots ,s_{k+1}\in {}^{{<}\omega }V_\lambda $
with
![]() $\operatorname {\mathrm {dom}}(s_0)=\ldots =\operatorname {\mathrm {dom}}(s_{k+1})$
and
$\operatorname {\mathrm {dom}}(s_0)=\ldots =\operatorname {\mathrm {dom}}(s_{k+1})$
and
![]() $r\in R_{T,\theta }(s_0,\ldots ,s_{k+1})^V$
, then the fact that
$r\in R_{T,\theta }(s_0,\ldots ,s_{k+1})^V$
, then the fact that
![]() $j_{0,\omega }(\theta )=\theta $
implies that
$j_{0,\omega }(\theta )=\theta $
implies that
![]() $j_{0,\omega }\circ r\in R_{T,\theta }(s_0,\ldots ,s_{k+1})^N$
. This inclusion allows us to define
$j_{0,\omega }\circ r\in R_{T,\theta }(s_0,\ldots ,s_{k+1})^N$
. This inclusion allows us to define
![]() ${\Lambda }:{S_{T,\theta }^V}\longrightarrow {S_{T,\theta }^N}$
to be the unique function with the property that for all
${\Lambda }:{S_{T,\theta }^V}\longrightarrow {S_{T,\theta }^N}$
to be the unique function with the property that for all
![]() $\langle s_0,\ldots ,s_k,t\rangle \in S_{T,\theta }^V$
and all
$\langle s_0,\ldots ,s_k,t\rangle \in S_{T,\theta }^V$
and all
![]() $s_{k+1}\in {}^{\operatorname {\mathrm {dom}}(s_0)}V_\lambda $
and
$s_{k+1}\in {}^{\operatorname {\mathrm {dom}}(s_0)}V_\lambda $
and
![]() $r\in R_{T,\theta }(s_0,\ldots ,s_{k+1})$
such that (3) holds for all
$r\in R_{T,\theta }(s_0,\ldots ,s_{k+1})$
such that (3) holds for all
![]() $\ell \in \operatorname {\mathrm {dom}}(t)$
, we have
$\ell \in \operatorname {\mathrm {dom}}(t)$
, we have
![]() $\Lambda (\langle s_0,\ldots ,s_k,t\rangle ) = \langle s_0,\ldots ,s_k,u\rangle $
, where
$\Lambda (\langle s_0,\ldots ,s_k,t\rangle ) = \langle s_0,\ldots ,s_k,u\rangle $
, where
for all
![]() $\ell \in \operatorname {\mathrm {dom}}(u)$
. This definition directly ensures that
$\ell \in \operatorname {\mathrm {dom}}(u)$
. This definition directly ensures that
![]() $\Lambda $
is an inclusion-preserving embedding.
$\Lambda $
is an inclusion-preserving embedding.
(iii) Since
![]() $S_{T,\theta }^N\subseteq S_{T,\theta }^V$
, we know that
$S_{T,\theta }^N\subseteq S_{T,\theta }^V$
, we know that
![]() $p[S_{T,\theta }^N]^V\subseteq p[S_{T,\theta }^V]^V$
. Pick a tuple
$p[S_{T,\theta }^N]^V\subseteq p[S_{T,\theta }^V]^V$
. Pick a tuple
![]() $\langle x_0,\ldots ,x_k,y\rangle $
in
$\langle x_0,\ldots ,x_k,y\rangle $
in
![]() $[S_{T,\theta }^V]^V$
and let z be the unique element of
$[S_{T,\theta }^V]^V$
and let z be the unique element of
![]() ${}^\omega V_{\theta +\omega }$
with
${}^\omega V_{\theta +\omega }$
with
for all
![]() $n<\omega $
. We then know that
$n<\omega $
. We then know that
![]() $\langle x_0,\ldots ,x_k,z\rangle $
is an element of
$\langle x_0,\ldots ,x_k,z\rangle $
is an element of
![]() $[S_{T,\theta }^N]^V$
. This shows that we also have
$[S_{T,\theta }^N]^V$
. This shows that we also have
![]() $p[S_{T,\theta }^V]^V\subseteq p[S_{T,\theta }^N]^V$
.
$p[S_{T,\theta }^V]^V\subseteq p[S_{T,\theta }^N]^V$
.
(iv) First, the fact that
![]() $S_{T,\theta }^N\subseteq S_{T,\theta }^V$
directly implies that
$S_{T,\theta }^N\subseteq S_{T,\theta }^V$
directly implies that
![]() $p[S_{T,\theta }^N]^N \subseteq p[S_{T,\theta }^V]^V\cap N$
. Now, fix
$p[S_{T,\theta }^N]^N \subseteq p[S_{T,\theta }^V]^V\cap N$
. Now, fix
![]() $\langle x_0,\ldots ,x_k\rangle \in p[S_{T,\theta }^V]^V\cap N$
and pick
$\langle x_0,\ldots ,x_k\rangle \in p[S_{T,\theta }^V]^V\cap N$
and pick
![]() $y\in V$
with
$y\in V$
with
![]() $\langle x_0,\ldots ,x_k,y\rangle \in [S_{T,\theta }^V]^V$
. Let z denote the unique element of
$\langle x_0,\ldots ,x_k,y\rangle \in [S_{T,\theta }^V]^V$
. Let z denote the unique element of
![]() ${}^{{<}\omega }V_{\theta +\omega }$
such that (4) holds for all
${}^{{<}\omega }V_{\theta +\omega }$
such that (4) holds for all
![]() $n<\omega $
. This shows that
$n<\omega $
. This shows that
![]() $\langle x_0,\ldots ,x_k,z\rangle \in [S_{T,\theta }^N]^V$
. Since the tuple
$\langle x_0,\ldots ,x_k,z\rangle \in [S_{T,\theta }^N]^V$
. Since the tuple
![]() $\langle x_0,\ldots ,x_k\rangle $
is an element of N, we know that
$\langle x_0,\ldots ,x_k\rangle $
is an element of N, we know that
is a tree of height
![]() $\omega $
in N and
$\omega $
in N and
![]() $z\in [U]^V$
. In this situation, the fact that the ill-foundedness of U is absolute between N and V yields an element
$z\in [U]^V$
. In this situation, the fact that the ill-foundedness of U is absolute between N and V yields an element
![]() $z^\prime $
of
$z^\prime $
of
![]() $[U]^N$
. We then have
$[U]^N$
. We then have
![]() $\langle x_0,\ldots ,x_k,z^\prime \rangle \in [S_{T,\theta }^N]^N$
and
$\langle x_0,\ldots ,x_k,z^\prime \rangle \in [S_{T,\theta }^N]^N$
and
![]() $\langle x_0,\ldots ,x_k\rangle \in p[S_{T,\theta }^N]^N$
.
$\langle x_0,\ldots ,x_k\rangle \in p[S_{T,\theta }^N]^N$
.
Corollary 3.6 [Reference Laver11, Theorem 1.4].
Let
![]() $\varphi (w_0,\ldots ,w_{n-1})$
be a
$\varphi (w_0,\ldots ,w_{n-1})$
be a
![]() $\Sigma _2^1$
-formula in the language of set theory with free second-order variables
$\Sigma _2^1$
-formula in the language of set theory with free second-order variables
![]() $w_0,\ldots ,w_{n-1}$
. If
$w_0,\ldots ,w_{n-1}$
. If
![]() ${j}:{V}\longrightarrow {M}$
is an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
is an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and N is an inner model of
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and N is an inner model of
![]() $\operatorname {\mathrm {ZFC}}$
with
$\operatorname {\mathrm {ZFC}}$
with
![]() $M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
, then the statement
$M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
, then the statement
is absolute between V and N for all
![]() $A_0,\ldots ,A_{n-1}\in V_{\lambda +1}^N$
, where
$A_0,\ldots ,A_{n-1}\in V_{\lambda +1}^N$
, where
![]() $\lambda =\sup _{n<\omega }\lambda _n$
.
$\lambda =\sup _{n<\omega }\lambda _n$
.
In order to connect the above concepts with the existence of perfect subsets, we now adapt a classical result of Mansfield (see [Reference Kanamori9, Theorem 14.7]) to our setting:
Lemma 3.7. Let
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of infinite cardinals with limit
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of infinite cardinals with limit
![]() $\lambda $
and let
$\lambda $
and let
![]() $T\subseteq {}^{{<}\omega } a\times {}^{{<}\omega } b$
be a tree with the property that
$T\subseteq {}^{{<}\omega } a\times {}^{{<}\omega } b$
be a tree with the property that
![]() $p[T]$
does not contain the range of a perfect embedding of
$p[T]$
does not contain the range of a perfect embedding of
![]() ${}^\omega \lambda $
into
${}^\omega \lambda $
into
![]() ${}^\omega a$
. If N is an inner model of
${}^\omega a$
. If N is an inner model of
![]() $\operatorname {\mathrm {ZFC}}$
with
$\operatorname {\mathrm {ZFC}}$
with
![]() $V_\lambda \cup \{T,\vec {\lambda }\}\subseteq N$
, then
$V_\lambda \cup \{T,\vec {\lambda }\}\subseteq N$
, then
![]() $p[T]^V\subseteq N$
.
$p[T]^V\subseteq N$
.
Proof. Given a tree
![]() $S\subseteq {}^{{<}\omega } a\times {}^{{<}\omega } b$
, we define
$S\subseteq {}^{{<}\omega } a\times {}^{{<}\omega } b$
, we define
![]() $S^\prime $
to be the set of all
$S^\prime $
to be the set of all
![]() $\langle t,u\rangle \in S$
with the property that for all
$\langle t,u\rangle \in S$
with the property that for all
![]() $n<\omega $
, there exists
$n<\omega $
, there exists
![]() $\operatorname {\mathrm {dom}}(t)<\ell <\omega $
such that the set
$\operatorname {\mathrm {dom}}(t)<\ell <\omega $
such that the set
has cardinality at least
![]() $\lambda _n$
. Then it is easy to see that for every such tree S, the set
$\lambda _n$
. Then it is easy to see that for every such tree S, the set
![]() $S^\prime $
is again a tree with
$S^\prime $
is again a tree with
![]() $S^\prime \subseteq S$
and, if S is an element of N, then
$S^\prime \subseteq S$
and, if S is an element of N, then
![]() $S^\prime $
is also contained N. Now, let
$S^\prime $
is also contained N. Now, let
![]() $\langle {T_\alpha }~\vert ~{\alpha \in \mathrm {{Ord}}}\rangle $
denote the unique sequence of trees with
$\langle {T_\alpha }~\vert ~{\alpha \in \mathrm {{Ord}}}\rangle $
denote the unique sequence of trees with
![]() $T_0=T$
,
$T_0=T$
,
![]() $T_{\alpha +1}=T_\alpha ^\prime $
for all
$T_{\alpha +1}=T_\alpha ^\prime $
for all
![]() $\alpha \in \mathrm {{Ord}}$
and
$\alpha \in \mathrm {{Ord}}$
and
![]() $T_\beta =\bigcap _{\alpha <\beta }T_\alpha $
for all
$T_\beta =\bigcap _{\alpha <\beta }T_\alpha $
for all
![]() $\beta \in \mathrm {{Lim}}$
. Then it is easy to see that
$\beta \in \mathrm {{Lim}}$
. Then it is easy to see that
![]() $T_\alpha \in N$
holds for all
$T_\alpha \in N$
holds for all
![]() $\alpha \in \mathrm {{Ord}}$
. Moreover, there exists
$\alpha \in \mathrm {{Ord}}$
. Moreover, there exists
![]() $\alpha _*\in \mathrm {{Ord}}$
with
$\alpha _*\in \mathrm {{Ord}}$
with
![]() $T_{\alpha _*}=T_\beta $
for all
$T_{\alpha _*}=T_\beta $
for all
![]() $\alpha _*\leq \beta \in \mathrm {{Ord}}$
. Set
$\alpha _*\leq \beta \in \mathrm {{Ord}}$
. Set
![]() $T_*=T_{\alpha _*}$
.
$T_*=T_{\alpha _*}$
.
Claim.
![]() $T_*=\emptyset $
.
$T_*=\emptyset $
.
Proof of the Claim.
Assume, towards a contradiction, that
![]() $T_*\neq \emptyset $
. Let
$T_*\neq \emptyset $
. Let
![]() $S_{\vec {\lambda }}$
denote the subtree of
$S_{\vec {\lambda }}$
denote the subtree of
![]() ${}^{{<}\omega }\lambda $
consisting of all
${}^{{<}\omega }\lambda $
consisting of all
![]() $s\in {}^{{<}\omega }\lambda $
with
$s\in {}^{{<}\omega }\lambda $
with
![]() $s(\ell )<\lambda _\ell $
for all
$s(\ell )<\lambda _\ell $
for all
![]() $\ell \in \operatorname {\mathrm {dom}}(s)$
. We inductively construct a system
$\ell \in \operatorname {\mathrm {dom}}(s)$
. We inductively construct a system
![]() $\langle {\langle s_u,t_u\rangle \in T_*}~\vert ~{u\in S_{\vec {\lambda }}}\rangle $
such that the following statements hold for all
$\langle {\langle s_u,t_u\rangle \in T_*}~\vert ~{u\in S_{\vec {\lambda }}}\rangle $
such that the following statements hold for all
![]() $u,v\in S_{\vec {\lambda }}$
:
$u,v\in S_{\vec {\lambda }}$
:
-
• If
 $u\subsetneq v$
, then
$u\subsetneq v$
, then
 $s_u\subsetneq s_v$
and
$s_u\subsetneq s_v$
and
 $t_u\subsetneq t_v$
.
$t_u\subsetneq t_v$
. -
• If
 $\alpha <\beta <\lambda _{\operatorname {\mathrm {dom}}(u)}$
, then
$\alpha <\beta <\lambda _{\operatorname {\mathrm {dom}}(u)}$
, then
 $\operatorname {\mathrm {dom}}(s_{u^\frown \langle \alpha \rangle })=\operatorname {\mathrm {dom}}(s_{u^\frown \langle \beta \rangle })$
and
$\operatorname {\mathrm {dom}}(s_{u^\frown \langle \alpha \rangle })=\operatorname {\mathrm {dom}}(s_{u^\frown \langle \beta \rangle })$
and
 $s_{u^\frown \langle \alpha \rangle }\neq s_{u^\frown \langle \beta \rangle }$
.
$s_{u^\frown \langle \alpha \rangle }\neq s_{u^\frown \langle \beta \rangle }$
.
First, define
![]() $s_\emptyset =t_\emptyset =\emptyset $
. Now, assume that
$s_\emptyset =t_\emptyset =\emptyset $
. Now, assume that
![]() $u\in S_{\vec {\lambda }}$
and
$u\in S_{\vec {\lambda }}$
and
![]() $\langle s_u,t_u\rangle \in T_*$
is already constructed. Since
$\langle s_u,t_u\rangle \in T_*$
is already constructed. Since
![]() $\langle s_u,t_u\rangle \in T_*^\prime =T_*$
, we can find
$\langle s_u,t_u\rangle \in T_*^\prime =T_*$
, we can find
![]() $\operatorname {\mathrm {dom}}(s_u)<\ell <\omega $
and a sequence
$\operatorname {\mathrm {dom}}(s_u)<\ell <\omega $
and a sequence
![]() $\langle {\langle s_\xi ,t_\xi \rangle \in T_*}~\vert ~{\xi <\lambda _{\operatorname {\mathrm {dom}}(u)}}\rangle $
with the property that for all
$\langle {\langle s_\xi ,t_\xi \rangle \in T_*}~\vert ~{\xi <\lambda _{\operatorname {\mathrm {dom}}(u)}}\rangle $
with the property that for all
![]() $\xi <\rho <\lambda _{\operatorname {\mathrm {dom}}(u)}$
, we have
$\xi <\rho <\lambda _{\operatorname {\mathrm {dom}}(u)}$
, we have
![]() $\operatorname {\mathrm {dom}}(s_\xi )=\operatorname {\mathrm {dom}}(s_\rho )=\ell $
and
$\operatorname {\mathrm {dom}}(s_\xi )=\operatorname {\mathrm {dom}}(s_\rho )=\ell $
and
![]() $s_\xi \neq s_\rho $
. Given
$s_\xi \neq s_\rho $
. Given
![]() $\xi <\lambda _{\operatorname {\mathrm {dom}}(u)}$
, we then define
$\xi <\lambda _{\operatorname {\mathrm {dom}}(u)}$
, we then define
![]() $s_{u^\frown \langle \xi \rangle }=s_\xi $
and
$s_{u^\frown \langle \xi \rangle }=s_\xi $
and
![]() $t_{u^\frown \langle \xi \rangle }=t_\xi $
. It then directly follows that the constructed sets satisfy all required properties. This completes the inductive construction of our system. If we now define
$t_{u^\frown \langle \xi \rangle }=t_\xi $
. It then directly follows that the constructed sets satisfy all required properties. This completes the inductive construction of our system. If we now define
then our setup ensures that
![]() $\iota $
is a perfect embedding. Moreover, we have
$\iota $
is a perfect embedding. Moreover, we have
for all
![]() $x\in C(\vec {\lambda })$
and this shows that
$x\in C(\vec {\lambda })$
and this shows that
![]() ${\mathrm {{ran}}(\iota )}$
is a subset of
${\mathrm {{ran}}(\iota )}$
is a subset of
![]() $p[T]$
. Since there exists a perfect embedding of
$p[T]$
. Since there exists a perfect embedding of
![]() ${}^\omega \lambda $
into
${}^\omega \lambda $
into
![]() $C(\vec {\lambda })$
, this yields a contradiction to our assumptions on T.
$C(\vec {\lambda })$
, this yields a contradiction to our assumptions on T.
Now, fix
![]() $\langle x,y\rangle \in [T]$
. Then there is an
$\langle x,y\rangle \in [T]$
. Then there is an
![]() $\alpha <\alpha _*$
with
$\alpha <\alpha _*$
with
![]() $\langle x,y\rangle \in [T_\alpha ]\setminus [T_{\alpha +1}]$
and we can find
$\langle x,y\rangle \in [T_\alpha ]\setminus [T_{\alpha +1}]$
and we can find
![]() $k<\omega $
with the property that
$k<\omega $
with the property that
![]() $\langle x\restriction k,y\restriction k\rangle \notin T_{\alpha +1}=T_\alpha ^\prime $
. Hence, there is
$\langle x\restriction k,y\restriction k\rangle \notin T_{\alpha +1}=T_\alpha ^\prime $
. Hence, there is
![]() $n<\omega $
with the property that for all
$n<\omega $
with the property that for all
![]() $k<\ell <\omega $
, the set
$k<\ell <\omega $
, the set
has cardinality less than
![]() $\lambda _n$
. Note that
$\lambda _n$
. Note that
![]() $x\restriction \ell \in E_\ell $
holds for all
$x\restriction \ell \in E_\ell $
holds for all
![]() $k<\ell <\omega $
. Moreover, since N contains the sequence
$k<\ell <\omega $
. Moreover, since N contains the sequence
![]() $\langle {E_\ell }~\vert ~{k<\ell <\omega }\rangle $
and each
$\langle {E_\ell }~\vert ~{k<\ell <\omega }\rangle $
and each
![]() $E_\ell $
has cardinality less than
$E_\ell $
has cardinality less than
![]() $\lambda _n$
in N, we can find a sequence
$\lambda _n$
in N, we can find a sequence
![]() $\langle {{\tau _\ell }:{\lambda _n}\longrightarrow {E_\ell }}~\vert ~{k<\ell <\omega }\rangle $
of surjections that is an element of N. If we pick
$\langle {{\tau _\ell }:{\lambda _n}\longrightarrow {E_\ell }}~\vert ~{k<\ell <\omega }\rangle $
of surjections that is an element of N. If we pick
![]() $z\in {}^\omega \lambda _n$
with
$z\in {}^\omega \lambda _n$
with
![]() $\tau _\ell (z(\ell ))=x\restriction \ell $
for all
$\tau _\ell (z(\ell ))=x\restriction \ell $
for all
![]() $k<\ell <\omega $
, then the fact that
$k<\ell <\omega $
, then the fact that
![]() $V_\lambda \subseteq N$
ensures that z is an element of N and hence we can conclude that x is also contained in the inner model N.
$V_\lambda \subseteq N$
ensures that z is an element of N and hence we can conclude that x is also contained in the inner model N.
We are now ready to prove the main result of this section.
Proof of Theorem 3.1.
Let
![]() ${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and let N be an inner model of
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and let N be an inner model of
![]() $\operatorname {\mathrm {ZFC}}$
with
$\operatorname {\mathrm {ZFC}}$
with
![]() $M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
. Set
$M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
. Set
![]() $\lambda =\sup _{n<\omega }\lambda _n$
. Fix a
$\lambda =\sup _{n<\omega }\lambda _n$
. Fix a
![]() $\Sigma ^1_1$
-formula
$\Sigma ^1_1$
-formula
![]() $\varphi (w_0,\ldots ,w_3)$
with second-order variables
$\varphi (w_0,\ldots ,w_3)$
with second-order variables
![]() $w_0,\ldots ,w_3$
and
$w_0,\ldots ,w_3$
and
![]() $B\in V_{\lambda +1}^N$
such that the set
$B\in V_{\lambda +1}^N$
such that the set
is a subset of
![]() $C(\vec {\lambda })$
of cardinality greater than
$C(\vec {\lambda })$
of cardinality greater than
![]() $(2^\lambda )^N$
. Set
$(2^\lambda )^N$
. Set
![]() $T=T^V_{\varphi ,B,\vec {\lambda }}$
,
$T=T^V_{\varphi ,B,\vec {\lambda }}$
,
![]() $\theta =(\lambda ^+)^V$
,
$\theta =(\lambda ^+)^V$
,
![]() $S_1=S_{T,\theta }^V$
and
$S_1=S_{T,\theta }^V$
and
![]() $S_0=S_{T,\theta }^N\subseteq S_1$
. An application of Lemma 3.5.iii then shows that
$S_0=S_{T,\theta }^N\subseteq S_1$
. An application of Lemma 3.5.iii then shows that
![]() $p[S_0]^V=p[S_1]^V$
. In particular, since Lemma 3.4 ensures that every element of X is of the form
$p[S_0]^V=p[S_1]^V$
. In particular, since Lemma 3.4 ensures that every element of X is of the form
![]() $\bigcup \{{y(n)}~\vert ~{n<\omega }\}$
for some
$\bigcup \{{y(n)}~\vert ~{n<\omega }\}$
for some
![]() $y\in p[S_1]^V$
, we know that
$y\in p[S_1]^V$
, we know that
![]() $p[S_0]^V$
has cardinality greater than
$p[S_0]^V$
has cardinality greater than
![]() $(2^\lambda )^N$
in V and we can conclude that
$(2^\lambda )^N$
in V and we can conclude that
![]() $p[S_0]^V\nsubseteq N$
. In this situation, an application of Lemma 3.7 shows that, in V, there exists a perfect embedding
$p[S_0]^V\nsubseteq N$
. In this situation, an application of Lemma 3.7 shows that, in V, there exists a perfect embedding
![]() ${\iota }:{{}^\omega \lambda }\longrightarrow {{}^\omega V_\lambda }$
satisfying
${\iota }:{{}^\omega \lambda }\longrightarrow {{}^\omega V_\lambda }$
satisfying
![]() ${\mathrm {{ran}}(\iota )}\subseteq p[S_0]=p[S_1]$
.
${\mathrm {{ran}}(\iota )}\subseteq p[S_0]=p[S_1]$
.
Now, work in V and define Y to be the set of all
![]() $y\in {}^\omega V_\lambda $
with the property that
$y\in {}^\omega V_\lambda $
with the property that
![]() $y(m)=y(n)\cap V_{\lambda _m}$
holds for all
$y(m)=y(n)\cap V_{\lambda _m}$
holds for all
![]() $m\leq n<\omega $
and
$m\leq n<\omega $
and
![]() $\bigcup \{{y(n)}~\vert ~{n<\omega }\}$
is an element of
$\bigcup \{{y(n)}~\vert ~{n<\omega }\}$
is an element of
![]() $C(\vec {\lambda })$
. Then Y is a closed subset of
$C(\vec {\lambda })$
. Then Y is a closed subset of
![]() ${}^\omega V_\lambda $
and
${}^\omega V_\lambda $
and
![]() $p[S_0]\subseteq Y$
. Moreover, the map
$p[S_0]\subseteq Y$
. Moreover, the map
is a homeomorphism of the subspace Y of
![]() ${}^\omega V_\omega $
and the space
${}^\omega V_\omega $
and the space
![]() $C(\vec {\lambda })$
with
$C(\vec {\lambda })$
with
![]() $\tau [p[S_0]]=X$
. In particular, there is a perfect embedding of
$\tau [p[S_0]]=X$
. In particular, there is a perfect embedding of
![]() ${}^\omega \lambda $
into
${}^\omega \lambda $
into
![]() $C(\vec {\lambda })$
whose range is contained in X.
$C(\vec {\lambda })$
whose range is contained in X.
Proof of Theorem 1.4.
Let
![]() ${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
${j}:{V}\longrightarrow {M}$
be an I2-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and set
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
and set
![]() $\lambda =\sup _{n<\omega }{\lambda _n}$
. Let X be a subset of
$\lambda =\sup _{n<\omega }{\lambda _n}$
. Let X be a subset of
![]() ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
![]() $\lambda $
that is definable by a
$\lambda $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $V_\lambda \cup \{V_\lambda ,\vec {\lambda }\}$
. In
$V_\lambda \cup \{V_\lambda ,\vec {\lambda }\}$
. In
![]() $M^j_\omega [\vec {\lambda }]$
, there is an injective enumeration
$M^j_\omega [\vec {\lambda }]$
, there is an injective enumeration
![]() $\vec {e}=\langle {d_\alpha }~\vert ~{\alpha <\lambda }\rangle $
of
$\vec {e}=\langle {d_\alpha }~\vert ~{\alpha <\lambda }\rangle $
of
![]() $V_\lambda $
with the property that
$V_\lambda $
with the property that
![]() $V_{\lambda _n}=\{{d_\alpha }~\vert ~{\alpha <\lambda _n}\}$
holds for all
$V_{\lambda _n}=\{{d_\alpha }~\vert ~{\alpha <\lambda _n}\}$
holds for all
![]() $n<\omega $
. Define Y to be the set of all
$n<\omega $
. Define Y to be the set of all
![]() $y\in C(\vec {\lambda })$
with the property that
$y\in C(\vec {\lambda })$
with the property that
![]() $y(0)=0$
and there exists
$y(0)=0$
and there exists
![]() $A\in X$
with
$A\in X$
with
![]() $d_{y(n+1)}=A\cap V_{\lambda _n}$
for all
$d_{y(n+1)}=A\cap V_{\lambda _n}$
for all
![]() $n<\omega $
. Then Y is a subset of
$n<\omega $
. Then Y is a subset of
![]() $C(\vec {\lambda })$
of cardinality greater than
$C(\vec {\lambda })$
of cardinality greater than
![]() $\lambda $
that is definable by a
$\lambda $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $M^j_\omega [\vec {\lambda }]\cap V_{\lambda +1}$
. Since
$M^j_\omega [\vec {\lambda }]\cap V_{\lambda +1}$
. Since
![]() $(2^\lambda )^{M^j_\omega [\vec {\lambda }]}<\lambda ^+$
, we can now combine Theorem 3.1 with Proposition 1.6 to find a perfect embedding of
$(2^\lambda )^{M^j_\omega [\vec {\lambda }]}<\lambda ^+$
, we can now combine Theorem 3.1 with Proposition 1.6 to find a perfect embedding of
![]() ${}^\omega \lambda $
into
${}^\omega \lambda $
into
![]() $C(\vec {\lambda })$
whose range is contained in Y. Using the fact that the subspace X of
$C(\vec {\lambda })$
whose range is contained in Y. Using the fact that the subspace X of
![]() ${\mathcal {P}}({\lambda })$
is homeomorphic to the subspace Y of
${\mathcal {P}}({\lambda })$
is homeomorphic to the subspace Y of
![]() $C(\vec {\lambda })$
, we can now conclude that there is a perfect embedding of
$C(\vec {\lambda })$
, we can now conclude that there is a perfect embedding of
![]() ${}^\omega \lambda $
into
${}^\omega \lambda $
into
![]() ${\mathcal {P}}({\lambda })$
whose range is contained in X.
${\mathcal {P}}({\lambda })$
whose range is contained in X.
4 The
 $\vec {\mathcal {U}}$
-Baire Property
$\vec {\mathcal {U}}$
-Baire Property
In [Reference Dimonte, Ros and Shi5], a new type of regularity property for higher function spaces is introduced: the
![]() $\lambda $
-Baire property. We can formalize this regularity property in a natural way as the
$\lambda $
-Baire property. We can formalize this regularity property in a natural way as the
![]() $\lambda $
-generalization of the classical Baire category notions:
$\lambda $
-generalization of the classical Baire category notions:
Definition 4.1 [Reference Dimonte, Ros and Shi5].
Let X be a topological space and let A be a subset of X.
-
(i) The set A is
 $\lambda $
-meager in X if it is a
$\lambda $
-meager in X if it is a
 $\lambda $
-union of nowhere dense sets.
$\lambda $
-union of nowhere dense sets. -
(ii) The set A is
 $\lambda $
-comeager in X if it is the complement of a
$\lambda $
-comeager in X if it is the complement of a
 $\lambda $
-meager set, i.e., if it contains the intersection of
$\lambda $
-meager set, i.e., if it contains the intersection of
 $\lambda $
-many open dense subsets of X.
$\lambda $
-many open dense subsets of X. -
(iii) The space X is a
 $\lambda $
-Baire space if every non-empty open subset of X is not
$\lambda $
-Baire space if every non-empty open subset of X is not
 $\lambda $
-meager.
$\lambda $
-meager. -
(iv) The set A has the
 $\lambda $
-Baire property in X if there exists an open set U in X such that the symmetric difference
$\lambda $
-Baire property in X if there exists an open set U in X such that the symmetric difference
 $A \, \Delta \, U$
is
$A \, \Delta \, U$
is
 $\lambda $
-meager.
$\lambda $
-meager.
Note that a space X is a
![]() $\lambda $
-Baire space if and only if the intersection of
$\lambda $
-Baire space if and only if the intersection of
![]() $\lambda $
-many open dense sets is dense. The definition of the
$\lambda $
-many open dense sets is dense. The definition of the
![]() $\vec {\mathcal {U}}$
-Baire property is more complex, as a direct generalization is unfruitfulFootnote
6
. It is strictly correlated to diagonal Prikry forcing (see, for example, [Reference Gitik7, Section 1.3]). In the following, fix a strictly increasing sequence
$\vec {\mathcal {U}}$
-Baire property is more complex, as a direct generalization is unfruitfulFootnote
6
. It is strictly correlated to diagonal Prikry forcing (see, for example, [Reference Gitik7, Section 1.3]). In the following, fix a strictly increasing sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of measurable cardinals with limit
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of measurable cardinals with limit
![]() $\lambda $
and a sequence
$\lambda $
and a sequence
![]() $\vec {\mathcal {U}}=\langle {U_n}~\vert ~{n<\omega }\rangle $
with the property that
$\vec {\mathcal {U}}=\langle {U_n}~\vert ~{n<\omega }\rangle $
with the property that
![]() $U_n$
is a normal ultrafilter on
$U_n$
is a normal ultrafilter on
![]() $\lambda _n$
for all
$\lambda _n$
for all
![]() $n<\omega $
.
$n<\omega $
.
Definition 4.2. The diagonal Prikry forcing with
![]() $\vec {\mathcal {U}}$
is the partial order
$\vec {\mathcal {U}}$
is the partial order
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
defined by the following clauses:
${\mathbb {P}_{\vec {\mathcal {U}}}}$
defined by the following clauses:
-
(i) Conditions in
 ${\mathbb {P}_{\vec {\mathcal {U}}}}$
are sequences
${\mathbb {P}_{\vec {\mathcal {U}}}}$
are sequences
 $p=\langle {p_n}~\vert ~{n<\omega }\rangle $
with the property that there exists
$p=\langle {p_n}~\vert ~{n<\omega }\rangle $
with the property that there exists
 $n<\omega $
such that
$n<\omega $
such that
 $p_i<\lambda _i$
for all
$p_i<\lambda _i$
for all
 $i<n$
and
$i<n$
and
 $p_i\in U_i$
for all
$p_i\in U_i$
for all
 $n\leq i<\omega $
. In this case, we set
$n\leq i<\omega $
. In this case, we set
 $s^p = \langle p_0,\dots ,p_{n-1}\rangle $
,
$s^p = \langle p_0,\dots ,p_{n-1}\rangle $
,
 $\operatorname {\mathrm {lh}}(p) = \operatorname {\mathrm {lh}}(s^p)$
, and
$\operatorname {\mathrm {lh}}(p) = \operatorname {\mathrm {lh}}(s^p)$
, and
 $A_i^p=p_i$
for all
$A_i^p=p_i$
for all
 $n\leq i<\omega $
. The sequence
$n\leq i<\omega $
. The sequence
 $s^p$
is also called the stem of p.
$s^p$
is also called the stem of p. -
(ii) Given conditions p and q in
 ${\mathbb {P}_{\vec {\mathcal {U}}}}$
, we have
${\mathbb {P}_{\vec {\mathcal {U}}}}$
, we have
 $p\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} q$
if and only if the following statements hold:
$p\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} q$
if and only if the following statements hold:-
•
 $\operatorname {\mathrm {lh}}(p) \geq \operatorname {\mathrm {lh}}(q)$
.
$\operatorname {\mathrm {lh}}(p) \geq \operatorname {\mathrm {lh}}(q)$
. -
•
 $s^p$
is an end-extension of
$s^p$
is an end-extension of
 $s^q$
.
$s^q$
. -
• If
 $\operatorname {\mathrm {lh}}(q) \leq i < \operatorname {\mathrm {lh}}(p)$
, then
$\operatorname {\mathrm {lh}}(q) \leq i < \operatorname {\mathrm {lh}}(p)$
, then
 $s^p(i) \in A^q_i$
.
$s^p(i) \in A^q_i$
. -
• If
 $\operatorname {\mathrm {lh}}(p)\leq i<\omega $
, then
$\operatorname {\mathrm {lh}}(p)\leq i<\omega $
, then
 $A^p_i \subseteq A^q_i$
.
$A^p_i \subseteq A^q_i$
.
Moreover, we say that
 $p \leq ^{*}_{{\mathbb {P}_{\vec {\mathcal {U}}}}} q$
if
$p \leq ^{*}_{{\mathbb {P}_{\vec {\mathcal {U}}}}} q$
if
 $p \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} q$
and
$p \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} q$
and
 $\operatorname {\mathrm {lh}}(p) = \operatorname {\mathrm {lh}}(q)$
.
$\operatorname {\mathrm {lh}}(p) = \operatorname {\mathrm {lh}}(q)$
. -
The intuition behind the definitions below is the following: it is easy to see that the product topology on the classical Baire space is isomorphic to the topology of the maximal filters on Cohen forcing. Thus, we are going to define a topology on
![]() $C(\vec {\lambda })$
that is isomorphic to the topology of the maximal filters on the diagonal Prikry forcing. Note that we can define this only if
$C(\vec {\lambda })$
that is isomorphic to the topology of the maximal filters on the diagonal Prikry forcing. Note that we can define this only if
![]() $\lambda $
is limit of measurable cardinals, therefore this will be the only setting for which to consider our new regularity property.
$\lambda $
is limit of measurable cardinals, therefore this will be the only setting for which to consider our new regularity property.
Definition 4.3.
-
(i) Given a condition p in
 ${\mathbb {P}_{\vec {\mathcal {U}}}}$
, we define
${\mathbb {P}_{\vec {\mathcal {U}}}}$
, we define  $$ \begin{align*}N_p & = \{{x \in \operatorname{\mathrm{C}}(\vec{\lambda})}~\vert~\forall i<\omega ~ [i < \operatorname{\mathrm{lh}}(p) \rightarrow x(i)\\ &= s^p(i) ~ \wedge ~ i\geq\operatorname{\mathrm{lh}}(p) \rightarrow x(i) \in A^p_j]\}.\end{align*} $$
$$ \begin{align*}N_p & = \{{x \in \operatorname{\mathrm{C}}(\vec{\lambda})}~\vert~\forall i<\omega ~ [i < \operatorname{\mathrm{lh}}(p) \rightarrow x(i)\\ &= s^p(i) ~ \wedge ~ i\geq\operatorname{\mathrm{lh}}(p) \rightarrow x(i) \in A^p_j]\}.\end{align*} $$
-
(ii) The Ellentuck-Prikry
 $\vec {\mathcal {U}}$
-topology on
$\vec {\mathcal {U}}$
-topology on
 $\operatorname{\mathrm{C}}(\vec{\lambda})$
(briefly,
$\operatorname{\mathrm{C}}(\vec{\lambda})$
(briefly,
 $\vec {\mathcal {U}}$
-EP topology) is the topology whose basic open sets are of the form
$\vec {\mathcal {U}}$
-EP topology) is the topology whose basic open sets are of the form
 $N_p$
for some condition p in
$N_p$
for some condition p in
 ${\mathbb {P}_{\vec {\mathcal {U}}}}$
.
${\mathbb {P}_{\vec {\mathcal {U}}}}$
. -
(iii) A subset A of
 $\operatorname{\mathrm{C}}(\vec{\lambda})$
has the
$\operatorname{\mathrm{C}}(\vec{\lambda})$
has the
 $\vec {\mathcal {U}}$
-Baire property if it has the
$\vec {\mathcal {U}}$
-Baire property if it has the
 $\lambda $
-Baire property in the
$\lambda $
-Baire property in the
 $\vec {\mathcal {U}}$
-EP topology.
$\vec {\mathcal {U}}$
-EP topology.
The results of [Reference Dimonte, Ros and Shi5] now show that the constructed topological spaces possess properties that generalize key properties of the classical Baire space to
![]() $\lambda $
:
$\lambda $
:
Proposition 4.4 (
 $\lambda $
-Baire Category, [Reference Dimonte, Ros and Shi5]).
$\lambda $
-Baire Category, [Reference Dimonte, Ros and Shi5]).
The space
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
endowed with the
$\operatorname{\mathrm{C}}(\vec{\lambda})$
endowed with the
![]() $\vec {\mathcal {U}}$
-EP topology is a
$\vec {\mathcal {U}}$
-EP topology is a
![]() $\lambda $
-Baire space. Moreover, every subset of
$\lambda $
-Baire space. Moreover, every subset of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
that is
$\operatorname{\mathrm{C}}(\vec{\lambda})$
that is
![]() $\lambda $
-comeager in the
$\lambda $
-comeager in the
![]() $\vec {\mathcal {U}}$
-EP topology contains a basic open set of this topology.
$\vec {\mathcal {U}}$
-EP topology contains a basic open set of this topology.
To motivate the main results of this section, we first show that the above property is non-trivial.
Theorem 4.5. There exists a subset of
![]() $C(\vec {\lambda })$
without the
$C(\vec {\lambda })$
without the
![]() $\vec {\mathcal {U}}$
-Baire property.
$\vec {\mathcal {U}}$
-Baire property.
The fact that the
![]() $\vec {\mathcal {U}}$
-EP topology is build using
$\vec {\mathcal {U}}$
-EP topology is build using
![]() $2^\lambda $
-many basic open subsets stops the proof of the above result from being a routine diagonalization argument. Instead, we have to use strong combinatorial properties of
$2^\lambda $
-many basic open subsets stops the proof of the above result from being a routine diagonalization argument. Instead, we have to use strong combinatorial properties of
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
to reduce the class of relevant open subsets.
${\mathbb {P}_{\vec {\mathcal {U}}}}$
to reduce the class of relevant open subsets.
Lemma 4.6 (Strong Prikry condition).
If D is a dense open subset of
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
and p is a condition in
${\mathbb {P}_{\vec {\mathcal {U}}}}$
and p is a condition in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
, then there exists a condition
${\mathbb {P}_{\vec {\mathcal {U}}}}$
, then there exists a condition
![]() $q\leq ^*_{{\mathbb {P}_{\vec {\mathcal {U}}}}}p$
and
$q\leq ^*_{{\mathbb {P}_{\vec {\mathcal {U}}}}}p$
and
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $r\in D$
holds for every condition
$r\in D$
holds for every condition
![]() $r\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}q$
with
$r\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}q$
with
![]() $\operatorname {\mathrm {lh}}(r)\geq n$
.
$\operatorname {\mathrm {lh}}(r)\geq n$
.
Corollary 4.7. If O is an open subset of
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
and p is a condition in
${\mathbb {P}_{\vec {\mathcal {U}}}}$
and p is a condition in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
, then there exists a condition
${\mathbb {P}_{\vec {\mathcal {U}}}}$
, then there exists a condition
![]() $\bar {p}\leq ^*_{{\mathbb {P}_{\vec {\mathcal {U}}}}}p$
such that if there exists a condition
$\bar {p}\leq ^*_{{\mathbb {P}_{\vec {\mathcal {U}}}}}p$
such that if there exists a condition
![]() $q \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} \bar {p}$
with
$q \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} \bar {p}$
with
![]() $q \in O$
, then
$q \in O$
, then
![]() $r \in O$
holds for every
$r \in O$
holds for every
![]() $r \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} \bar {p}$
with
$r \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} \bar {p}$
with
![]() $\operatorname {\mathrm {lh}}(r)\geq \operatorname {\mathrm {lh}}(q)$
.
$\operatorname {\mathrm {lh}}(r)\geq \operatorname {\mathrm {lh}}(q)$
.
Given a set P of conditions in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
, we let
${\mathbb {P}_{\vec {\mathcal {U}}}}$
, we let
denote the corresponding open set in the
![]() $\vec {\mathcal {U}}$
-EP topology.
$\vec {\mathcal {U}}$
-EP topology.
Proposition 4.8. A set P of condition in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
is predense in the partial order
${\mathbb {P}_{\vec {\mathcal {U}}}}$
is predense in the partial order
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
if and only if
${\mathbb {P}_{\vec {\mathcal {U}}}}$
if and only if
![]() $U_P$
is dense in the
$U_P$
is dense in the
![]() $\vec {\mathcal {U}}$
-EP topology.
$\vec {\mathcal {U}}$
-EP topology.
Proof. First, assume that P is predense in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
and fix a condition p in
${\mathbb {P}_{\vec {\mathcal {U}}}}$
and fix a condition p in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
. Then there exists a condition q in P and a condition r in
${\mathbb {P}_{\vec {\mathcal {U}}}}$
. Then there exists a condition q in P and a condition r in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
![]() $r\leq _{\mathbb {P}_{\vec {\mathcal {U}}}} p,q$
. We now know that
$r\leq _{\mathbb {P}_{\vec {\mathcal {U}}}} p,q$
. We now know that
![]() $\emptyset \neq N_r\subseteq N_p\cap N_q\subseteq N_p\cap U_P$
.
$\emptyset \neq N_r\subseteq N_p\cap N_q\subseteq N_p\cap U_P$
.
Now, assume that
![]() $U_P$
is dense in the
$U_P$
is dense in the
![]() $\vec {\mathcal {U}}$
-EP topology and fix a condition p in
$\vec {\mathcal {U}}$
-EP topology and fix a condition p in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
. Since
${\mathbb {P}_{\vec {\mathcal {U}}}}$
. Since
![]() $N_p\cap U_P\neq \emptyset $
, we can find a condition q in P and an element x of
$N_p\cap U_P\neq \emptyset $
, we can find a condition q in P and an element x of
![]() $C(\vec {\lambda })$
with
$C(\vec {\lambda })$
with
![]() $x\in N_p\cap N_q$
. Then there exists a condition r in
$x\in N_p\cap N_q$
. Then there exists a condition r in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
![]() $r_i=x(i)$
for all
$r_i=x(i)$
for all
![]() $i<\max (\operatorname {\mathrm {lh}}(p),\operatorname {\mathrm {lh}}(q))$
and
$i<\max (\operatorname {\mathrm {lh}}(p),\operatorname {\mathrm {lh}}(q))$
and
![]() $A^r_i=A^p_i\cap A^q_i$
for all
$A^r_i=A^p_i\cap A^q_i$
for all
![]() $\max (\operatorname {\mathrm {lh}}(p),\operatorname {\mathrm {lh}}(q))\leq i<\omega $
. We then know that
$\max (\operatorname {\mathrm {lh}}(p),\operatorname {\mathrm {lh}}(q))\leq i<\omega $
. We then know that
![]() $r\leq _{\mathbb {P}_{\vec {\mathcal {U}}}} p,q$
holds. These computations show that P is predense in
$r\leq _{\mathbb {P}_{\vec {\mathcal {U}}}} p,q$
holds. These computations show that P is predense in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
.
${\mathbb {P}_{\vec {\mathcal {U}}}}$
.
Lemma 4.9. If U is an open set in the
![]() $\vec {\mathcal {U}}$
-EP topology, then there exists a set P of at most
$\vec {\mathcal {U}}$
-EP topology, then there exists a set P of at most
![]() $\lambda $
-many conditions in
$\lambda $
-many conditions in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
such that
${\mathbb {P}_{\vec {\mathcal {U}}}}$
such that
![]() $U_P\subseteq U$
and
$U_P\subseteq U$
and
![]() $U\setminus U_P$
is nowhere dense in the
$U\setminus U_P$
is nowhere dense in the
![]() $\vec {\mathcal {U}}$
-EP topology.
$\vec {\mathcal {U}}$
-EP topology.
Proof. Define O to be the set of all conditions p in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
with the property that
${\mathbb {P}_{\vec {\mathcal {U}}}}$
with the property that
![]() $N_p\subseteq U$
. Then O is an open subset of
$N_p\subseteq U$
. Then O is an open subset of
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
. In addition, define S to be the set of all conditions p in
${\mathbb {P}_{\vec {\mathcal {U}}}}$
. In addition, define S to be the set of all conditions p in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
such that
${\mathbb {P}_{\vec {\mathcal {U}}}}$
such that
![]() $p_i=\lambda _i$
holds for all
$p_i=\lambda _i$
holds for all
![]() $\operatorname {\mathrm {lh}}(p)\leq i<\omega $
. In this situation, Corollary 4.7 shows that for every
$\operatorname {\mathrm {lh}}(p)\leq i<\omega $
. In this situation, Corollary 4.7 shows that for every
![]() $p\in P$
, we can then find a condition
$p\in P$
, we can then find a condition
![]() $\bar {p}\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}^*p$
with the property that if there is a condition
$\bar {p}\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}^*p$
with the property that if there is a condition
![]() $q \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} \bar {p}$
with
$q \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} \bar {p}$
with
![]() $q \in O$
, then
$q \in O$
, then
![]() $r \in O$
holds for every
$r \in O$
holds for every
![]() $r \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} \bar {p}$
with
$r \leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}} \bar {p}$
with
![]() $\operatorname {\mathrm {lh}}(r)\geq \operatorname {\mathrm {lh}}(q)$
. Define
$\operatorname {\mathrm {lh}}(r)\geq \operatorname {\mathrm {lh}}(q)$
. Define
The fact that the set S has cardinality
![]() $\lambda $
then ensures that P consists of at most
$\lambda $
then ensures that P consists of at most
![]() $\lambda $
-many conditions in
$\lambda $
-many conditions in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
.
${\mathbb {P}_{\vec {\mathcal {U}}}}$
.
Claim.
![]() $U_P\subseteq U$
.
$U_P\subseteq U$
.
Proof of the Claim.
Pick
![]() $p\in S$
with the property that there is
$p\in S$
with the property that there is
![]() $q\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}\bar {p}$
with
$q\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}\bar {p}$
with
![]() $q\in O$
and fix
$q\in O$
and fix
![]() $x\in N_{\bar {p}}$
. Then there exists a condition
$x\in N_{\bar {p}}$
. Then there exists a condition
![]() $r\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}\bar {p}$
with
$r\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}\bar {p}$
with
![]() $r_i=x(i)$
for all
$r_i=x(i)$
for all
![]() $i<\operatorname {\mathrm {lh}}(q)$
and
$i<\operatorname {\mathrm {lh}}(q)$
and
![]() $r_i=A^{\bar {p}}_i$
for all
$r_i=A^{\bar {p}}_i$
for all
![]() $\operatorname {\mathrm {lh}}(r)\leq i<\omega $
. Since
$\operatorname {\mathrm {lh}}(r)\leq i<\omega $
. Since
![]() $\operatorname {\mathrm {lh}}(q)=\operatorname {\mathrm {lh}}(r)$
, we then know that
$\operatorname {\mathrm {lh}}(q)=\operatorname {\mathrm {lh}}(r)$
, we then know that
![]() $r\in O$
and
$r\in O$
and
![]() $x\in N_r\subseteq U$
.
$x\in N_r\subseteq U$
.
Claim. If
![]() $p\in S$
with
$p\in S$
with
![]() $q\notin O$
for all
$q\notin O$
for all
![]() $q\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}\bar {p}$
, then
$q\leq _{{\mathbb {P}_{\vec {\mathcal {U}}}}}\bar {p}$
, then
![]() $N_{\bar {p}}\cap U=\emptyset $
.
$N_{\bar {p}}\cap U=\emptyset $
.
Proof of the Claim.
Assume, towards a contradiction, that there is an
![]() $x\in N_{\bar {p}}\cap U$
. Pick a condition q in
$x\in N_{\bar {p}}\cap U$
. Pick a condition q in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
![]() $x\in N_q\subseteq U$
. Then there exists a condition r in
$x\in N_q\subseteq U$
. Then there exists a condition r in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
![]() $r_i=x(i)$
for all
$r_i=x(i)$
for all
![]() $i<\max (\operatorname {\mathrm {lh}}(\bar {p}),\operatorname {\mathrm {lh}}(q))$
and
$i<\max (\operatorname {\mathrm {lh}}(\bar {p}),\operatorname {\mathrm {lh}}(q))$
and
![]() $r_i=A^{\bar {p}}_i\cap A^q_i$
for all
$r_i=A^{\bar {p}}_i\cap A^q_i$
for all
![]() $\max (\operatorname {\mathrm {lh}}(\bar {p}),\operatorname {\mathrm {lh}}(q))\leq i<\omega $
. We then know that
$\max (\operatorname {\mathrm {lh}}(\bar {p}),\operatorname {\mathrm {lh}}(q))\leq i<\omega $
. We then know that
![]() $r\leq _{\mathbb {P}_{\vec {\mathcal {U}}}} \bar {p},q$
and
$r\leq _{\mathbb {P}_{\vec {\mathcal {U}}}} \bar {p},q$
and
![]() $x\in N_r\subseteq N_q\subseteq U$
. But this implies that r is an element of O below
$x\in N_r\subseteq N_q\subseteq U$
. But this implies that r is an element of O below
![]() $\bar {p}$
, a contradiction.
$\bar {p}$
, a contradiction.
Define u to be the unique condition in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
${\mathbb {P}_{\vec {\mathcal {U}}}}$
with
![]() $\operatorname {\mathrm {lh}}(u)=0$
and
$\operatorname {\mathrm {lh}}(u)=0$
and
for all
![]() $i<\omega $
. In addition, set
$i<\omega $
. In addition, set
Claim. The set N is nowhere dense in the
![]() $\vec {\mathcal {U}}$
-EP topology.
$\vec {\mathcal {U}}$
-EP topology.
Proof of the Claim.
Assume, towards a contradiction, that N is dense in
![]() $N_p$
for some condition p in
$N_p$
for some condition p in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
. Let
${\mathbb {P}_{\vec {\mathcal {U}}}}$
. Let
![]() $q\leq ^*_{{\mathbb {P}_{\vec {\mathcal {U}}}}}p$
be the unique condition with
$q\leq ^*_{{\mathbb {P}_{\vec {\mathcal {U}}}}}p$
be the unique condition with
![]() $A^q_i=A^p_i\cap A^u_i$
for all
$A^q_i=A^p_i\cap A^u_i$
for all
![]() $\operatorname {\mathrm {lh}}(p)\leq i<\omega $
. Then there is
$\operatorname {\mathrm {lh}}(p)\leq i<\omega $
. Then there is
![]() $x\in N\cap N_q$
and we can find
$x\in N\cap N_q$
and we can find
![]() $\operatorname {\mathrm {lh}}(q)\leq i<\omega $
with
$\operatorname {\mathrm {lh}}(q)\leq i<\omega $
with
![]() $x(i)\notin A^u_i$
. But, this implies that
$x(i)\notin A^u_i$
. But, this implies that
![]() $x(i)\notin A^q_i$
, a contradiction.
$x(i)\notin A^q_i$
, a contradiction.
Claim.
![]() $U\setminus U_P\subseteq N$
.
$U\setminus U_P\subseteq N$
.
Proof of the Claim.
Pick
![]() $x\in U\setminus U_P$
and fix
$x\in U\setminus U_P$
and fix
![]() $j<\omega $
. Let p denote the unique element of S with
$j<\omega $
. Let p denote the unique element of S with
![]() $s^p=x\restriction j$
. Then
$s^p=x\restriction j$
. Then
![]() $x\notin N_{\bar {p}}$
, because otherwise we would have
$x\notin N_{\bar {p}}$
, because otherwise we would have
![]() $x\in N_{\bar {p}}\cap U\neq \emptyset $
and our second claim would imply that
$x\in N_{\bar {p}}\cap U\neq \emptyset $
and our second claim would imply that
![]() $N_{\bar {p}}\subseteq U_P$
. Since
$N_{\bar {p}}\subseteq U_P$
. Since
![]() $\bar {p}\leq ^*_{{\mathbb {P}_{\vec {\mathcal {U}}}}}p$
, we can now find
$\bar {p}\leq ^*_{{\mathbb {P}_{\vec {\mathcal {U}}}}}p$
, we can now find
![]() $j\leq i<\omega $
with
$j\leq i<\omega $
with
![]() $x(i)\notin A^{\bar {p}}_i$
. Our definitions then ensure that
$x(i)\notin A^{\bar {p}}_i$
. Our definitions then ensure that
![]() $A_i^u\subseteq A^{\bar {p}}_i$
and we can conclude that
$A_i^u\subseteq A^{\bar {p}}_i$
and we can conclude that
![]() $x(i)\notin A^u_i$
. These computations show that x is an element of N.
$x(i)\notin A^u_i$
. These computations show that x is an element of N.
This last claim completes the proof of the lemma.
Proof of Theorem 4.5.
Define
![]() $\mathcal {O}$
to be the collection of all subsets of
$\mathcal {O}$
to be the collection of all subsets of
![]() $C(\vec {\lambda })$
of the form
$C(\vec {\lambda })$
of the form
![]() $U_P$
for some set P of at most
$U_P$
for some set P of at most
![]() $\lambda $
-many conditions in
$\lambda $
-many conditions in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
. Then the set
${\mathbb {P}_{\vec {\mathcal {U}}}}$
. Then the set
![]() $\mathcal {O}$
has cardinality at most
$\mathcal {O}$
has cardinality at most
![]() $2^\lambda $
and we can fix an enumeration
$2^\lambda $
and we can fix an enumeration
![]() $\langle {\langle U_\gamma ,M_\gamma \rangle }~\vert ~{\gamma <2^\lambda }\rangle $
of all pairs
$\langle {\langle U_\gamma ,M_\gamma \rangle }~\vert ~{\gamma <2^\lambda }\rangle $
of all pairs
![]() $\langle U,M\rangle $
such that
$\langle U,M\rangle $
such that
![]() $U\in \mathcal {O}$
and there exists a sequence
$U\in \mathcal {O}$
and there exists a sequence
![]() $\langle {O_\alpha }~\vert ~{\alpha <\lambda }\rangle $
of dense elements of
$\langle {O_\alpha }~\vert ~{\alpha <\lambda }\rangle $
of dense elements of
![]() $\mathcal {O}$
with
$\mathcal {O}$
with
![]() $M=\bigcup _{\alpha <\lambda }(C(\vec {\lambda })\setminus O_\alpha )$
. We inductively define increasing sequences
$M=\bigcup _{\alpha <\lambda }(C(\vec {\lambda })\setminus O_\alpha )$
. We inductively define increasing sequences
![]() $\langle {A_\gamma }~\vert ~{\gamma <2^\lambda }\rangle $
and
$\langle {A_\gamma }~\vert ~{\gamma <2^\lambda }\rangle $
and
![]() $\langle {B_\gamma }~\vert ~{\gamma <2^\lambda }\rangle $
of subsets of
$\langle {B_\gamma }~\vert ~{\gamma <2^\lambda }\rangle $
of subsets of
![]() $C(\lambda )$
with
$C(\lambda )$
with
![]() $A_\gamma \cap B_\gamma =\emptyset $
and
$A_\gamma \cap B_\gamma =\emptyset $
and
![]() $\vert A_\gamma \cup B_\gamma \vert \leq \vert \gamma \vert $
for all
$\vert A_\gamma \cup B_\gamma \vert \leq \vert \gamma \vert $
for all
![]() $\gamma <2^\lambda $
. Fix
$\gamma <2^\lambda $
. Fix
![]() $\gamma <2^\lambda $
and assume that we already defined
$\gamma <2^\lambda $
and assume that we already defined
![]() $A_\beta $
and
$A_\beta $
and
![]() $B_\beta $
for all
$B_\beta $
for all
![]() $\beta <\gamma $
. Set
$\beta <\gamma $
. Set
![]() $A=\bigcup _{\beta <\gamma }A_\beta $
and
$A=\bigcup _{\beta <\gamma }A_\beta $
and
![]() $B=\bigcup _{\beta <\gamma }B_\beta $
. Then
$B=\bigcup _{\beta <\gamma }B_\beta $
. Then
![]() $A\cap B=\emptyset $
and both sets have cardinality less than
$A\cap B=\emptyset $
and both sets have cardinality less than
![]() $2^\lambda $
. First, assume that
$2^\lambda $
. First, assume that
![]() $U_\gamma $
is empty. Since Proposition 4.4 ensures that
$U_\gamma $
is empty. Since Proposition 4.4 ensures that
![]() $C(\vec {\lambda })\setminus M_\gamma $
has cardinality
$C(\vec {\lambda })\setminus M_\gamma $
has cardinality
![]() $2^\lambda $
, we can find
$2^\lambda $
, we can find
![]() $x\in C(\vec {\lambda })\setminus (B\cup M_\gamma )$
. We then define
$x\in C(\vec {\lambda })\setminus (B\cup M_\gamma )$
. We then define
![]() $A_\gamma =A\cup \{x\}$
and
$A_\gamma =A\cup \{x\}$
and
![]() $B_\gamma =B$
. Next, assume that
$B_\gamma =B$
. Next, assume that
![]() $U_\gamma $
is non-empty. Then Proposition 4.4 shows that
$U_\gamma $
is non-empty. Then Proposition 4.4 shows that
![]() $U_\gamma \setminus M_\gamma $
has cardinality
$U_\gamma \setminus M_\gamma $
has cardinality
![]() $2^\lambda $
and we can find
$2^\lambda $
and we can find
![]() $x\in U_\gamma \setminus (A\cup M_\gamma )$
. We now define
$x\in U_\gamma \setminus (A\cup M_\gamma )$
. We now define
![]() $A_\gamma =A$
and
$A_\gamma =A$
and
![]() $B_\gamma =B\cup \{x\}$
. This completes our construction.
$B_\gamma =B\cup \{x\}$
. This completes our construction.
Define
![]() $A=\bigcup _{\gamma <2^\lambda }A_\gamma $
and
$A=\bigcup _{\gamma <2^\lambda }A_\gamma $
and
![]() $B=\bigcup _{\gamma <2^\lambda }B_\gamma $
. Then
$B=\bigcup _{\gamma <2^\lambda }B_\gamma $
. Then
![]() $A\cap B=\emptyset $
. Assume, towards a contradiction, that the set A has the
$A\cap B=\emptyset $
. Assume, towards a contradiction, that the set A has the
![]() $\vec {\mathcal {U}}$
-Baire property. Pick an open subset U in the
$\vec {\mathcal {U}}$
-Baire property. Pick an open subset U in the
![]() $\vec {\mathcal {U}}$
-EP topology such that
$\vec {\mathcal {U}}$
-EP topology such that
![]() $A \, \Delta \, U$
is
$A \, \Delta \, U$
is
![]() $\lambda $
-meager in this topology. Then Lemma 4.9 shows that there exists
$\lambda $
-meager in this topology. Then Lemma 4.9 shows that there exists
![]() $W\in \mathcal {O}$
with
$W\in \mathcal {O}$
with
![]() $W\subseteq U$
and
$W\subseteq U$
and
![]() $U\setminus W$
nowhere dense. It follows that
$U\setminus W$
nowhere dense. It follows that
![]() $A \, \Delta \, W$
is also
$A \, \Delta \, W$
is also
![]() $\lambda $
-meager. Another application of Lemma 4.9 then yields a sequence
$\lambda $
-meager. Another application of Lemma 4.9 then yields a sequence
![]() $\langle {O_\alpha }~\vert ~{\alpha <\lambda }\rangle $
of dense elements of
$\langle {O_\alpha }~\vert ~{\alpha <\lambda }\rangle $
of dense elements of
![]() $\mathcal {O}$
with
$\mathcal {O}$
with
![]() $A \, \Delta \, W\subseteq \bigcup _{\alpha <\lambda }(C(\vec {\lambda })\setminus O_\alpha )$
. In this situation, there exists a
$A \, \Delta \, W\subseteq \bigcup _{\alpha <\lambda }(C(\vec {\lambda })\setminus O_\alpha )$
. In this situation, there exists a
![]() $\gamma <2^\lambda $
with
$\gamma <2^\lambda $
with
![]() $U_\gamma =W$
and
$U_\gamma =W$
and
![]() $M_\gamma =\bigcup _{\alpha <\lambda }(C(\vec {\lambda })\setminus O_\alpha )$
. Then
$M_\gamma =\bigcup _{\alpha <\lambda }(C(\vec {\lambda })\setminus O_\alpha )$
. Then
![]() $U_\gamma \neq \emptyset $
, because otherwise our construction would ensure that there is
$U_\gamma \neq \emptyset $
, because otherwise our construction would ensure that there is
![]() $x\in A\setminus W$
with
$x\in A\setminus W$
with
![]() $x\notin M_\gamma $
. But this means that there is
$x\notin M_\gamma $
. But this means that there is
![]() $x\in B\cap U_\gamma $
with
$x\in B\cap U_\gamma $
with
![]() $x\notin M_\gamma $
and therefore
$x\notin M_\gamma $
and therefore
![]() $x\in A\cap B$
, a contradiction.
$x\in A\cap B$
, a contradiction.
We now proceed by showing that, in the model constructed in the proof of Theorem 2.3, the above constructions can also be used to find a simply definable set without the
![]() $\vec {\mathcal {U}}$
-Baire property.
$\vec {\mathcal {U}}$
-Baire property.
Theorem 4.10. If
![]() ${j}:{V}\longrightarrow {M}$
is an I2-embedding whose critical sequence has supremum
${j}:{V}\longrightarrow {M}$
is an I2-embedding whose critical sequence has supremum
![]() $\lambda $
, then the following statements hold in an inner model:
$\lambda $
, then the following statements hold in an inner model:
-
(i) There is an I2-embedding whose critical sequence has supremum
 $\lambda $
.
$\lambda $
. -
(ii) If
 $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
is a strictly increasing sequence of measurable cardinal with limit
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
is a strictly increasing sequence of measurable cardinal with limit
 $\lambda $
and
$\lambda $
and
 $\vec {\mathcal {U}}=\langle {U_n}~\vert ~{n<\omega }\rangle $
is a sequence with the property that
$\vec {\mathcal {U}}=\langle {U_n}~\vert ~{n<\omega }\rangle $
is a sequence with the property that
 $U_n$
is a normal ultrafilter on
$U_n$
is a normal ultrafilter on
 $\lambda _n$
for all
$\lambda _n$
for all
 $n<\omega $
, then there is a subset z of
$n<\omega $
, then there is a subset z of
 $\lambda $
and a subset X of
$\lambda $
and a subset X of
 $C(\vec {\lambda })$
such that X does not have the
$C(\vec {\lambda })$
such that X does not have the
 $\vec {\mathcal {U}}$
-Baire property and the set X is definable by a
$\vec {\mathcal {U}}$
-Baire property and the set X is definable by a
 $\Sigma _1$
-formula with parameter z.
$\Sigma _1$
-formula with parameter z.
Proof. As in the proof of Theorem 2.3, pick a subset y of
![]() $\lambda $
with
$\lambda $
with
![]() $V_\lambda \cup \{j\restriction V_\lambda \}\subseteq L[y]$
and work in
$V_\lambda \cup \{j\restriction V_\lambda \}\subseteq L[y]$
and work in
![]() $L[y]$
. Then there is an I2-embedding whose critical sequence has supremum
$L[y]$
. Then there is an I2-embedding whose critical sequence has supremum
![]() $\lambda $
. Fix a strictly increasing sequence
$\lambda $
. Fix a strictly increasing sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of measurable cardinals with limit
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
of measurable cardinals with limit
![]() $\lambda $
and a sequence
$\lambda $
and a sequence
![]() $\vec {\mathcal {U}}=\langle {U_n}~\vert ~{n<\omega }\rangle $
with the property that
$\vec {\mathcal {U}}=\langle {U_n}~\vert ~{n<\omega }\rangle $
with the property that
![]() $U_n$
is a normal ultrafilter on
$U_n$
is a normal ultrafilter on
![]() $\lambda _n$
for all
$\lambda _n$
for all
![]() $n<\omega $
. We can now find an unbounded subset z of
$n<\omega $
. We can now find an unbounded subset z of
![]() $\lambda $
with the property that the
$\lambda $
with the property that the
![]() $\{\vec {\mathcal {U}}\}$
is definable by a
$\{\vec {\mathcal {U}}\}$
is definable by a
![]() $\Sigma _1$
-formula with parameter z and there is a well-ordering
$\Sigma _1$
-formula with parameter z and there is a well-ordering
![]() $\lhd $
of
$\lhd $
of
![]() ${H}_{{\lambda ^+}}$
of order-type
${H}_{{\lambda ^+}}$
of order-type
![]() $\lambda ^+$
with the property that the set of all proper initial segments of
$\lambda ^+$
with the property that the set of all proper initial segments of
![]() $\lhd $
is definable by a
$\lhd $
is definable by a
![]() $\Sigma _1$
-formula with parameter z. It then directly follows that the set
$\Sigma _1$
-formula with parameter z. It then directly follows that the set
![]() $\{\vec {\mathcal {U}}\}$
, the set of all conditions in
$\{\vec {\mathcal {U}}\}$
, the set of all conditions in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
, the ordering of
${\mathbb {P}_{\vec {\mathcal {U}}}}$
, the ordering of
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
, the compatibility relation of
${\mathbb {P}_{\vec {\mathcal {U}}}}$
, the compatibility relation of
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
and the incompatibility relation of
${\mathbb {P}_{\vec {\mathcal {U}}}}$
and the incompatibility relation of
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
are all
${\mathbb {P}_{\vec {\mathcal {U}}}}$
are all
![]() $\Delta _1$
-definable from the parameter z.
$\Delta _1$
-definable from the parameter z.
Now, define
![]() $\mathcal {O}$
to be the set of all pairs
$\mathcal {O}$
to be the set of all pairs
![]() $\langle P,\vec {Q}\rangle $
with the property that P is a set of at most
$\langle P,\vec {Q}\rangle $
with the property that P is a set of at most
![]() $\lambda $
-many conditions in
$\lambda $
-many conditions in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
and
${\mathbb {P}_{\vec {\mathcal {U}}}}$
and
![]() $\vec {Q}=\langle {Q_\alpha }~\vert ~{\alpha <\lambda }\rangle $
is a sequence with the property that each
$\vec {Q}=\langle {Q_\alpha }~\vert ~{\alpha <\lambda }\rangle $
is a sequence with the property that each
![]() $Q_\alpha $
is a set of at most
$Q_\alpha $
is a set of at most
![]() $\lambda $
-many conditions in
$\lambda $
-many conditions in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
. It is then easy to see that
${\mathbb {P}_{\vec {\mathcal {U}}}}$
. It is then easy to see that
![]() $\mathcal {O}$
is a subset of
$\mathcal {O}$
is a subset of
![]() ${H}_{{\lambda ^+}}$
of cardinality
${H}_{{\lambda ^+}}$
of cardinality
![]() $\lambda ^+$
that is definable by a
$\lambda ^+$
that is definable by a
![]() $\Sigma _1$
-formula with parameter z. Let
$\Sigma _1$
-formula with parameter z. Let
![]() $\langle {\langle P_\gamma ,\langle {Q^\gamma _\alpha }~\vert ~{\alpha <\lambda }\rangle \rangle }~\vert ~{\gamma <\lambda ^+}\rangle $
denote the enumeration of
$\langle {\langle P_\gamma ,\langle {Q^\gamma _\alpha }~\vert ~{\alpha <\lambda }\rangle \rangle }~\vert ~{\gamma <\lambda ^+}\rangle $
denote the enumeration of
![]() $\mathcal {O}$
induced by
$\mathcal {O}$
induced by
![]() $\lhd $
. We then again know that this sequence is definable by a
$\lhd $
. We then again know that this sequence is definable by a
![]() $\Sigma _1$
-formula with parameter z. Arguing as in the proof of Theorem 4.5, we can now use Proposition 4.8 to show that for every
$\Sigma _1$
-formula with parameter z. Arguing as in the proof of Theorem 4.5, we can now use Proposition 4.8 to show that for every
![]() $\gamma <\lambda ^+$
with the property that
$\gamma <\lambda ^+$
with the property that
![]() $Q^\gamma _\alpha $
is predense in
$Q^\gamma _\alpha $
is predense in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
for all
${\mathbb {P}_{\vec {\mathcal {U}}}}$
for all
![]() $\alpha <\lambda $
, the set
$\alpha <\lambda $
, the set
![]() $\bigcap _{\alpha <\lambda }U_{Q^\gamma _\alpha }$
has cardinality
$\bigcap _{\alpha <\lambda }U_{Q^\gamma _\alpha }$
has cardinality
![]() $\lambda ^+$
. Moreover, we know that for every
$\lambda ^+$
. Moreover, we know that for every
![]() $\gamma <\lambda ^+$
with the property that
$\gamma <\lambda ^+$
with the property that
![]() $P_\gamma \neq \emptyset $
and
$P_\gamma \neq \emptyset $
and
![]() $Q^\gamma _\alpha $
is predense in
$Q^\gamma _\alpha $
is predense in
![]() ${\mathbb {P}_{\vec {\mathcal {U}}}}$
for all
${\mathbb {P}_{\vec {\mathcal {U}}}}$
for all
![]() $\alpha <\lambda $
, the set
$\alpha <\lambda $
, the set
![]() $U_P\cap \bigcap _{\alpha <\lambda }U_{Q^\gamma _\alpha }$
has cardinality
$U_P\cap \bigcap _{\alpha <\lambda }U_{Q^\gamma _\alpha }$
has cardinality
![]() $\lambda ^+$
. This shows that there is a unique sequence
$\lambda ^+$
. This shows that there is a unique sequence
![]() $\langle {d_\gamma }~\vert ~{\gamma <\lambda ^+}\rangle $
with the property that for all
$\langle {d_\gamma }~\vert ~{\gamma <\lambda ^+}\rangle $
with the property that for all
![]() $\gamma <\lambda ^+$
, the set
$\gamma <\lambda ^+$
, the set
![]() $d_\gamma $
is the
$d_\gamma $
is the
![]() $\lhd $
-least element of
$\lhd $
-least element of
![]() ${H}_{{\lambda ^+}}$
such that one of the following statements hold:
${H}_{{\lambda ^+}}$
such that one of the following statements hold:
-
• The set
 $d_\gamma $
is of the form
$d_\gamma $
is of the form
 $\langle 0,p\rangle $
, where p is a condition in
$\langle 0,p\rangle $
, where p is a condition in
 ${\mathbb {P}_{\vec {\mathcal {U}}}}$
with the property that there exists an
${\mathbb {P}_{\vec {\mathcal {U}}}}$
with the property that there exists an
 $\alpha <\lambda $
such that all conditions in
$\alpha <\lambda $
such that all conditions in
 $Q^\gamma _\alpha $
are incompatible with p in
$Q^\gamma _\alpha $
are incompatible with p in
 ${\mathbb {P}_{\vec {\mathcal {U}}}}$
.
${\mathbb {P}_{\vec {\mathcal {U}}}}$
. -
•
 $P_\gamma $
is the empty set and the set
$P_\gamma $
is the empty set and the set
 $d_\gamma $
is of the form
$d_\gamma $
is of the form
 $\langle 1,x\rangle $
, where x is an element of
$\langle 1,x\rangle $
, where x is an element of
 $\bigcap _{\alpha <\lambda }U_{Q^\gamma _\alpha }$
with the property that
$\bigcap _{\alpha <\lambda }U_{Q^\gamma _\alpha }$
with the property that
 $x\neq v$
holds whenever
$x\neq v$
holds whenever
 $\beta <\gamma $
and
$\beta <\gamma $
and
 $d_\beta $
is of the form
$d_\beta $
is of the form
 $\langle 2,v\rangle $
for some v in
$\langle 2,v\rangle $
for some v in
 $C(\vec {\lambda })$
.
$C(\vec {\lambda })$
. -
• The set
 $d_\gamma $
is of the form
$d_\gamma $
is of the form
 $\langle 2,x\rangle $
, where x is an element of
$\langle 2,x\rangle $
, where x is an element of
 $U_{P_\gamma }\cap \bigcap _{\alpha <\lambda }U_{Q^\gamma _\alpha }$
with the property that
$U_{P_\gamma }\cap \bigcap _{\alpha <\lambda }U_{Q^\gamma _\alpha }$
with the property that
 $x\neq u$
holds whenever
$x\neq u$
holds whenever
 $\beta <\gamma $
and
$\beta <\gamma $
and
 $d_\beta $
is of the form
$d_\beta $
is of the form
 $\langle 1,u\rangle $
for some u in
$\langle 1,u\rangle $
for some u in
 $C(\vec {\lambda })$
.
$C(\vec {\lambda })$
.
This definition then ensures that the sequence
![]() $\langle {d_\gamma }~\vert ~{\gamma <\lambda ^+}\rangle $
is definable by a
$\langle {d_\gamma }~\vert ~{\gamma <\lambda ^+}\rangle $
is definable by a
![]() $\Sigma _1$
-formula with parameter z. We define
$\Sigma _1$
-formula with parameter z. We define
Then A is definable by a
![]() $\Sigma _1$
-formula with parameter z and, by repeating the computations made in the proof of Theorem 4.5, we can show that A does not have the
$\Sigma _1$
-formula with parameter z and, by repeating the computations made in the proof of Theorem 4.5, we can show that A does not have the
![]() $\vec {\mathcal {U}}$
-Baire property.
$\vec {\mathcal {U}}$
-Baire property.
Contrary to the perfect set property case, there are no previous results about the possibility of
![]() $\Sigma _1$
- or
$\Sigma _1$
- or
![]() $\Sigma ^1_2$
-definable sets to have this kind of regularity property. In the following, we will again focus on the structural consequences of large cardinal assumptions close to the Kunen inconsistency. The following lemma will allow us to prove an analogue to Theorem 3.1 for the
$\Sigma ^1_2$
-definable sets to have this kind of regularity property. In the following, we will again focus on the structural consequences of large cardinal assumptions close to the Kunen inconsistency. The following lemma will allow us to prove an analogue to Theorem 3.1 for the
![]() $\vec {\mathcal {U}}$
-Baire property.
$\vec {\mathcal {U}}$
-Baire property.
Lemma 4.11. Let
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of measurable cardinals with supremum
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of measurable cardinals with supremum
![]() $\lambda $
and let N be an inner model of
$\lambda $
and let N be an inner model of
![]() $\operatorname {\mathrm {ZFC}}$
with
$\operatorname {\mathrm {ZFC}}$
with
![]() $V_\lambda \cup \{\vec {\lambda }\}\subseteq N$
and
$V_\lambda \cup \{\vec {\lambda }\}\subseteq N$
and
![]() $(2^\lambda )^N<\lambda ^+$
. If
$(2^\lambda )^N<\lambda ^+$
. If
![]() $\vec {\mathcal {U}}=\langle {U_n}~\vert ~{n<\omega }\rangle $
is a sequence in N with the property that
$\vec {\mathcal {U}}=\langle {U_n}~\vert ~{n<\omega }\rangle $
is a sequence in N with the property that
![]() $U_n$
is a normal ultrafilter on
$U_n$
is a normal ultrafilter on
![]() $\lambda _n$
for all
$\lambda _n$
for all
![]() $n<\omega $
and
$n<\omega $
and
then C is
![]() $\lambda $
-comeager in the
$\lambda $
-comeager in the
![]() $\vec {\mathcal {U}}$
-EP topology.
$\vec {\mathcal {U}}$
-EP topology.
Proof. By the Mathias condition for the diagonal Prikry forcing (see [Reference Fuchs6]), the set C consists of all
![]() $x\in C(\vec {\lambda })$
with the property that for every sequence
$x\in C(\vec {\lambda })$
with the property that for every sequence
![]() $\vec {A}= \langle {A_n \in U_n}~\vert ~{n < \omega }\rangle $
in N, the function x belongs to the dense open set
$\vec {A}= \langle {A_n \in U_n}~\vert ~{n < \omega }\rangle $
in N, the function x belongs to the dense open set
Since
![]() $(2^\lambda )^N<\lambda ^+$
, there are only
$(2^\lambda )^N<\lambda ^+$
, there are only
![]() $\lambda $
-many dense open sets of this form and Proposition 4.4 yields the desired conclusion.
$\lambda $
-many dense open sets of this form and Proposition 4.4 yields the desired conclusion.
We are now ready to prove our analogue to Theorem 3.1.
Theorem 4.12. Let
![]() ${j}:{V}\longrightarrow {M}$
be an I2-elementary embedding with
${j}:{V}\longrightarrow {M}$
be an I2-elementary embedding with
![]() $\lambda $
being the supremum of its critical sequence
$\lambda $
being the supremum of its critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n < \omega }\rangle $
and let N be an inner model of
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n < \omega }\rangle $
and let N be an inner model of
![]() $\operatorname {\mathrm {ZFC}}$
with
$\operatorname {\mathrm {ZFC}}$
with
![]() $M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
and
$M^j_\omega \cup \{\vec {\lambda }\}\subseteq N$
and
![]() $(2^\lambda )^N<\lambda ^+$
. Then there exists a sequence
$(2^\lambda )^N<\lambda ^+$
. Then there exists a sequence
![]() $\vec {\mathcal {F}}=\langle {F_n}~\vert ~{n<\omega }\rangle $
in N such that each
$\vec {\mathcal {F}}=\langle {F_n}~\vert ~{n<\omega }\rangle $
in N such that each
![]() $F_n$
is a normal ultrafilter on
$F_n$
is a normal ultrafilter on
![]() $\lambda _n$
and every subset of
$\lambda _n$
and every subset of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
that is definable over
$\operatorname{\mathrm{C}}(\vec{\lambda})$
that is definable over
![]() $V_\lambda $
by a
$V_\lambda $
by a
![]() $\Sigma ^1_2$
-formula with parameters in
$\Sigma ^1_2$
-formula with parameters in
![]() $V^N_{\lambda +1}$
has the
$V^N_{\lambda +1}$
has the
![]() $\vec {\mathcal {F}}$
-Baire property.
$\vec {\mathcal {F}}$
-Baire property.
Proof. Since
![]() $V_\lambda \subseteq M^j_\omega \subseteq N$
,
$V_\lambda \subseteq M^j_\omega \subseteq N$
,
![]() $\vec {\lambda }\in N$
and each
$\vec {\lambda }\in N$
and each
![]() $\lambda _n$
is a measurable cardinal in N, we can pick a sequence
$\lambda _n$
is a measurable cardinal in N, we can pick a sequence
![]() $\vec {\mathcal {F}}=\langle {F_n}~\vert ~{n<\omega }\rangle $
in N such that each
$\vec {\mathcal {F}}=\langle {F_n}~\vert ~{n<\omega }\rangle $
in N such that each
![]() $F_n$
is a normal ultrafilter on
$F_n$
is a normal ultrafilter on
![]() $\lambda _n$
. Note that every condition in
$\lambda _n$
. Note that every condition in
![]() $\mathbb {P}_{\vec {\mathcal {F}}}^N$
is a condition in
$\mathbb {P}_{\vec {\mathcal {F}}}^N$
is a condition in
![]() $\mathbb {P}_{\vec {\mathcal {F}}}^V$
. In V, we define
$\mathbb {P}_{\vec {\mathcal {F}}}^V$
. In V, we define
Then Lemma 4.11 shows that C is
![]() $\lambda $
-comeager in the
$\lambda $
-comeager in the
![]() $\vec {\mathcal {F}}$
-EP topology.
$\vec {\mathcal {F}}$
-EP topology.
Fix a
![]() $\Sigma ^1_2$
-formula
$\Sigma ^1_2$
-formula
![]() $\varphi (w_0,w_1)$
with second-order variables
$\varphi (w_0,w_1)$
with second-order variables
![]() $w_0$
and
$w_0$
and
![]() $w_1$
and
$w_1$
and
![]() $B\in V_{\lambda +1}^N$
such that the set
$B\in V_{\lambda +1}^N$
such that the set
is a subset of
![]() $C(\vec {\lambda })$
. Define O to be the set of all conditions p in
$C(\vec {\lambda })$
. Define O to be the set of all conditions p in
![]() $\mathbb {P}_{\vec {\mathcal {F}}}^N$
with
$\mathbb {P}_{\vec {\mathcal {F}}}^N$
with
where
![]() $\dot {x}$
denotes the canonical
$\dot {x}$
denotes the canonical
![]() $\mathbb {P}_{\vec {\mathcal {F}}}^N$
-name for the generic sequence in N.
$\mathbb {P}_{\vec {\mathcal {F}}}^N$
-name for the generic sequence in N.
Work in V and define U to be the union of all sets of the form
![]() $N_p$
with
$N_p$
with
![]() $p\in O$
. Fix
$p\in O$
. Fix
![]() $x\in C$
. First, assume that
$x\in C$
. First, assume that
![]() $x\in U$
and fix
$x\in U$
and fix
![]() $p\in O$
with
$p\in O$
with
![]() $x\in N_p$
. Since
$x\in N_p$
. Since
is the filter on
![]() $\mathbb {P}_{\vec {\mathcal {F}}}^N$
induced by x, we then know that
$\mathbb {P}_{\vec {\mathcal {F}}}^N$
induced by x, we then know that
holds in
![]() $N[x]$
and therefore Corollary 3.6 shows that x is an element of X. In the other direction, assume that
$N[x]$
and therefore Corollary 3.6 shows that x is an element of X. In the other direction, assume that
![]() $x\in X$
. Then (6) holds in V and Corollary 3.6 ensures that this statement also holds in
$x\in X$
. Then (6) holds in V and Corollary 3.6 ensures that this statement also holds in
![]() $N[x]$
. Then there is a condition p in
$N[x]$
. Then there is a condition p in
![]() $G_x$
with the property that (5) holds. But then
$G_x$
with the property that (5) holds. But then
![]() $p\in O$
,
$p\in O$
,
![]() $x\in N_p$
and hence
$x\in N_p$
and hence
![]() $x\in U$
. These computations now show that the sets U and
$x\in U$
. These computations now show that the sets U and
![]() $C(\vec {\lambda })\setminus C$
witness that X has the
$C(\vec {\lambda })\setminus C$
witness that X has the
![]() $\vec {\mathcal {F}}$
-Baire property.
$\vec {\mathcal {F}}$
-Baire property.
A quick analysis of the proof shows that the consequences of the above theorem hold for every
![]() $\vec {\mathcal {F}}\in N$
.
$\vec {\mathcal {F}}\in N$
.
Note that, since
![]() $(2^\lambda )^{M^j_\omega [\vec {\lambda }]}<\lambda ^+$
holds in the situation of the above theorem, there exists a sequence
$(2^\lambda )^{M^j_\omega [\vec {\lambda }]}<\lambda ^+$
holds in the situation of the above theorem, there exists a sequence
![]() $\vec {\mathcal {F}}$
of normal measures such that every subset of
$\vec {\mathcal {F}}$
of normal measures such that every subset of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
that is definable over
$\operatorname{\mathrm{C}}(\vec{\lambda})$
that is definable over
![]() $V_\lambda $
by a
$V_\lambda $
by a
![]() $\Sigma ^1_2$
-formula with parameters in
$\Sigma ^1_2$
-formula with parameters in
![]() $V_\lambda \cup \{\vec {\lambda }\}$
has the
$V_\lambda \cup \{\vec {\lambda }\}$
has the
![]() $\vec {\mathcal {F}}$
-Baire property.
$\vec {\mathcal {F}}$
-Baire property.
In the remainder of this paper, we study the interaction of I0-embeddings with the
![]() $\lambda $
-Baire property of families of sets. One of the key ingredients of the proof of Theorem 4.12 is Corollary 3.6, that states that there is a certain amount of absoluteness between V and models that contain
$\lambda $
-Baire property of families of sets. One of the key ingredients of the proof of Theorem 4.12 is Corollary 3.6, that states that there is a certain amount of absoluteness between V and models that contain
![]() $M_{\omega }^j[\vec {\lambda }]$
. Woodin and Cramer proved that I0-embeddings also entail absoluteness-like results.
$M_{\omega }^j[\vec {\lambda }]$
. Woodin and Cramer proved that I0-embeddings also entail absoluteness-like results.
Remember that, given a limit ordinal
![]() $\lambda $
, we define
$\lambda $
, we define
This concept generalizes the definition of
![]() $\Theta $
for
$\Theta $
for
![]() $L(\mathbb {R})$
. Since
$L(\mathbb {R})$
. Since
![]() $L(\mathbb {R})$
is not going to appear in this paper and there is no risk of confusion, we will below write
$L(\mathbb {R})$
is not going to appear in this paper and there is no risk of confusion, we will below write
![]() $\Theta $
instead of
$\Theta $
instead of
![]() $\Theta ^{L(V_{\lambda +1})}$
. An ordinal
$\Theta ^{L(V_{\lambda +1})}$
. An ordinal
![]() $\alpha <\Theta $
is called good if every element of
$\alpha <\Theta $
is called good if every element of
![]() $L_\alpha (V_{\lambda +1})$
is definable over
$L_\alpha (V_{\lambda +1})$
is definable over
![]() $L_\alpha (V_{\lambda +1})$
from an element of
$L_\alpha (V_{\lambda +1})$
from an element of
![]() $V_{\lambda +1}$
. The next theorem is called Generic Absoluteness in [Reference Hugh Woodin18].
$V_{\lambda +1}$
. The next theorem is called Generic Absoluteness in [Reference Hugh Woodin18].
Theorem 4.13 (Woodin, [Reference Cramer2, Theorem 82]).
Let
![]() ${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
be an I0-embedding that is
${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
be an I0-embedding that is
![]() $\omega $
-iterable and let
$\omega $
-iterable and let
![]() ${j_{0,\omega }}:{L(V_{\lambda +1})}\longrightarrow {M_{\omega }}$
be the embedding into the
${j_{0,\omega }}:{L(V_{\lambda +1})}\longrightarrow {M_{\omega }}$
be the embedding into the
![]() $\omega $
-th iterate of
$\omega $
-th iterate of
![]() $L(V_{\lambda +1})$
by j. Assume that
$L(V_{\lambda +1})$
by j. Assume that
![]() $\mathbb {P}\in M_\omega $
is a partial order and
$\mathbb {P}\in M_\omega $
is a partial order and
![]() $g\in V$
is
$g\in V$
is
![]() $\mathbb {P}$
-generic over
$\mathbb {P}$
-generic over
![]() $M_\omega $
with
$M_\omega $
with
![]() ${\mathrm {{cof}}({\lambda })}^{M_\omega [g]}=\omega $
. If
${\mathrm {{cof}}({\lambda })}^{M_\omega [g]}=\omega $
. If
![]() $\alpha <\Theta $
is good, then for some
$\alpha <\Theta $
is good, then for some
![]() $\bar \alpha < \lambda $
, there is an elementary embedding
$\bar \alpha < \lambda $
, there is an elementary embedding
that is the identity below
![]() $\lambda $
.
$\lambda $
.
Note that, in the situation of the above theorem the good ordinals are cofinal in
![]() $\Theta $
(see [Reference Laver12]). Moreover, if there exists an I0-embedding, then there exists an iterable I0-embedding (see [Reference Hugh Woodin18, Lemmas 10 and 21]). Therefore, the hypothesis of the above result is not restrictive.
$\Theta $
(see [Reference Laver12]). Moreover, if there exists an I0-embedding, then there exists an iterable I0-embedding (see [Reference Hugh Woodin18, Lemmas 10 and 21]). Therefore, the hypothesis of the above result is not restrictive.
Theorem 4.14. Let
![]() ${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
be an I0-embedding with critical sequence
${j}:{L(V_{\lambda +1})}\longrightarrow {L(V_{\lambda +1})}$
be an I0-embedding with critical sequence
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
. Then there exists a sequence
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
. Then there exists a sequence
![]() $\vec {\mathcal {F}}=\langle {F_n}~\vert ~{n<\omega }\rangle $
such that each
$\vec {\mathcal {F}}=\langle {F_n}~\vert ~{n<\omega }\rangle $
such that each
![]() $F_n$
is a normal ultrafilter on
$F_n$
is a normal ultrafilter on
![]() $\lambda _n$
and every subset of
$\lambda _n$
and every subset of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
that is definable over
$\operatorname{\mathrm{C}}(\vec{\lambda})$
that is definable over
![]() $V_\lambda $
by a
$V_\lambda $
by a
![]() $\Sigma ^1_n$
-formula with parameters in
$\Sigma ^1_n$
-formula with parameters in
![]() $V_{\lambda +1}$
has the
$V_{\lambda +1}$
has the
![]() $\vec {\mathcal {F}}$
-Baire property.
$\vec {\mathcal {F}}$
-Baire property.
Proof. By earlier remarks, we may assume that j is
![]() $\omega $
-iterable. In the following, we let
$\omega $
-iterable. In the following, we let
![]() ${j_{0,\omega }}:{L(V_{\lambda +1})}\longrightarrow {M_{\omega }}$
denote the embedding into the
${j_{0,\omega }}:{L(V_{\lambda +1})}\longrightarrow {M_{\omega }}$
denote the embedding into the
![]() $\omega $
-th iterate of
$\omega $
-th iterate of
![]() $L(V_{\lambda +1})$
by j. Then
$L(V_{\lambda +1})$
by j. Then
![]() $\vec {\lambda }$
is Prikry-generic over
$\vec {\lambda }$
is Prikry-generic over
![]() $M_\omega $
and there is a sequence
$M_\omega $
and there is a sequence
![]() $\vec {\mathcal {F}}=\langle {F_n}~\vert ~{n<\omega }\rangle $
in
$\vec {\mathcal {F}}=\langle {F_n}~\vert ~{n<\omega }\rangle $
in
![]() $M_\omega [\vec {\lambda }]$
such that each
$M_\omega [\vec {\lambda }]$
such that each
![]() $F_n$
is a normal ultrafilter on
$F_n$
is a normal ultrafilter on
![]() $\lambda _n$
. Finally, we define
$\lambda _n$
. Finally, we define
![]() $\mathbb {P}$
to be the corresponding diagonal Prikry forcing
$\mathbb {P}$
to be the corresponding diagonal Prikry forcing
![]() $\mathbb {P}_{\vec {\mathcal {F}}}^{M_\omega [\vec {\lambda }]}$
in
$\mathbb {P}_{\vec {\mathcal {F}}}^{M_\omega [\vec {\lambda }]}$
in
![]() $M_\omega [\vec {\lambda }]$
.
$M_\omega [\vec {\lambda }]$
.
Given
![]() $n<\omega $
, we fix a
$n<\omega $
, we fix a
![]() $\Sigma ^1_n$
-formula
$\Sigma ^1_n$
-formula
![]() $\varphi (w_0,w_1)$
in the language of set theory with free second-order variables
$\varphi (w_0,w_1)$
in the language of set theory with free second-order variables
![]() $w_0$
and
$w_0$
and
![]() $w_1$
. Given
$w_1$
. Given
![]() $y \in M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1}$
, we define
$y \in M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1}$
, we define
As in the proof of Theorem 4.12, we now define
![]() $O_{\varphi ,y}$
to be the open subset of
$O_{\varphi ,y}$
to be the open subset of
![]() $\mathbb {P}$
in
$\mathbb {P}$
in
![]() $M_\omega [\vec {\lambda }]$
that consists of all conditions p with
$M_\omega [\vec {\lambda }]$
that consists of all conditions p with
where
![]() $\dot {x}$
denotes the canonical
$\dot {x}$
denotes the canonical
![]() $\mathbb {P}$
-name for the generic sequence in
$\mathbb {P}$
-name for the generic sequence in
![]() $M_\omega [\vec {j}]$
. In addition, we let
$M_\omega [\vec {j}]$
. In addition, we let
![]() $U_{\varphi ,y}$
denote the union of all sets
$U_{\varphi ,y}$
denote the union of all sets
![]() $N_p$
with
$N_p$
with
![]() $p\in O_{\varphi ,y}$
in V. Finally, we define C to be the set of all x in
$p\in O_{\varphi ,y}$
in V. Finally, we define C to be the set of all x in
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
that are
$\operatorname{\mathrm{C}}(\vec{\lambda})$
that are
![]() $\mathbb {P}$
-generic over
$\mathbb {P}$
-generic over
![]() $M_\omega [\vec {\lambda }]$
. Since
$M_\omega [\vec {\lambda }]$
. Since
![]() $(2^\lambda )^{M_\omega [\vec {\lambda }]}<\lambda ^+$
, an application of Lemma 4.11 shows that C is
$(2^\lambda )^{M_\omega [\vec {\lambda }]}<\lambda ^+$
, an application of Lemma 4.11 shows that C is
![]() $\lambda $
-comeager in the
$\lambda $
-comeager in the
![]() $\vec {\mathcal {F}}$
-EP topology.
$\vec {\mathcal {F}}$
-EP topology.
Now, fix x in C. Still following the proof of Theorem 4.12, we then know that x is an element of
![]() $U_{\varphi ,y}$
if and only if
$U_{\varphi ,y}$
if and only if
holds in
![]() $M_\omega [\vec {\lambda },x]$
. The model
$M_\omega [\vec {\lambda },x]$
. The model
![]() $M_{\omega }[\vec {\lambda },x]$
is a generic extension (via the forcing that is a two-step iteration of Prikry and diagonal Prikry forcing) of
$M_{\omega }[\vec {\lambda },x]$
is a generic extension (via the forcing that is a two-step iteration of Prikry and diagonal Prikry forcing) of
![]() $M_\omega $
and
$M_\omega $
and
![]() ${\mathrm {{cof}}({\lambda })}^{M_\omega [\vec {\lambda },x]}=\omega $
. Therefore, we can apply Generic Absoluteness to
${\mathrm {{cof}}({\lambda })}^{M_\omega [\vec {\lambda },x]}=\omega $
. Therefore, we can apply Generic Absoluteness to
![]() $M_{\omega }[\vec {\lambda },x]$
to show that
$M_{\omega }[\vec {\lambda },x]$
to show that
![]() $x\in U_{\varphi ,y}$
if and only if
$x\in U_{\varphi ,y}$
if and only if
![]() $x \in X_{\varphi ,y} $
. These computations show that
$x \in X_{\varphi ,y} $
. These computations show that
![]() $U_{\varphi ,y} \, \Delta \, X_{\varphi ,y}\subseteq C(\vec {\lambda })\setminus C$
and we can conclude that the set
$U_{\varphi ,y} \, \Delta \, X_{\varphi ,y}\subseteq C(\vec {\lambda })\setminus C$
and we can conclude that the set
![]() $X_{\varphi ,y}$
has the
$X_{\varphi ,y}$
has the
![]() $\vec {\mathcal {F}}$
-Baire property.
$\vec {\mathcal {F}}$
-Baire property.
We now know that the statement
holds in
![]() $L(V_{\lambda +1})$
for every
$L(V_{\lambda +1})$
for every
![]() $\Sigma ^1_n$
-formula
$\Sigma ^1_n$
-formula
![]() $\varphi (w_0,w_1)$
and for all
$\varphi (w_0,w_1)$
and for all
![]() $y \in M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1}$
. We claim that this statement can be expressed by a formula that only uses a single existential quantifier bounded by the set
$y \in M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1}$
. We claim that this statement can be expressed by a formula that only uses a single existential quantifier bounded by the set
![]() $V_{\lambda +2}$
of all subsets of
$V_{\lambda +2}$
of all subsets of
![]() $V_{\lambda +1}$
. Notice that, as a consequence of this, it follows that the
$V_{\lambda +1}$
. Notice that, as a consequence of this, it follows that the
![]() $\vec {\mathcal {F}}$
-Baire property is upward absolute. By definition of
$\vec {\mathcal {F}}$
-Baire property is upward absolute. By definition of
![]() $\vec {\mathcal {F}}$
-Baire property, the set
$\vec {\mathcal {F}}$
-Baire property, the set
![]() $X_{\varphi ,y}$
has the
$X_{\varphi ,y}$
has the
![]() $\vec {\mathcal {F}}$
-Baire property if and only if there exist an open subset U of
$\vec {\mathcal {F}}$
-Baire property if and only if there exist an open subset U of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
and a sequence
$\operatorname{\mathrm{C}}(\vec{\lambda})$
and a sequence
![]() $\langle {C_\alpha }~\vert ~{\alpha < \lambda }\rangle $
of closed nowhere dense subsets of
$\langle {C_\alpha }~\vert ~{\alpha < \lambda }\rangle $
of closed nowhere dense subsets of
![]() $\operatorname{\mathrm{C}}(\vec{\lambda})$
with the property that
$\operatorname{\mathrm{C}}(\vec{\lambda})$
with the property that
![]() $A \, \Delta \, U \subseteq \bigcup _{\alpha < \lambda } C_\alpha $
. Notice now that each open set W is determined by the subset
$A \, \Delta \, U \subseteq \bigcup _{\alpha < \lambda } C_\alpha $
. Notice now that each open set W is determined by the subset
![]() $\{{p\in \mathbb {P}_{\vec {\mathcal {F}}}}~\vert ~{N_p \subseteq W}\}$
of
$\{{p\in \mathbb {P}_{\vec {\mathcal {F}}}}~\vert ~{N_p \subseteq W}\}$
of
![]() $V_{\lambda +1}$
. Hence, the set U and the sequence
$V_{\lambda +1}$
. Hence, the set U and the sequence
![]() $\langle {C_\alpha }~\vert ~{\alpha < \lambda }\rangle $
can be determined by a
$\langle {C_\alpha }~\vert ~{\alpha < \lambda }\rangle $
can be determined by a
![]() $\lambda $
-sequence of subsets of
$\lambda $
-sequence of subsets of
![]() $V_{\lambda +1}$
, which in turn can be canonically identified with a subset of
$V_{\lambda +1}$
, which in turn can be canonically identified with a subset of
![]() $V_{\lambda +1}$
. It is now easy to see that the claim holds.
$V_{\lambda +1}$
. It is now easy to see that the claim holds.
Now, given
![]() $y \in V_{\lambda +1}$
with the property that (7) holds in
$y \in V_{\lambda +1}$
with the property that (7) holds in
![]() $L(V_{\lambda +1})$
, we define
$L(V_{\lambda +1})$
, we define
![]() $\alpha _y$
to be the least ordinal
$\alpha _y$
to be the least ordinal
![]() $\alpha $
below
$\alpha $
below
![]() $\Theta $
such that (7) holds in
$\Theta $
such that (7) holds in
![]() $L_\alpha (V_{\lambda +1})$
. Such an ordinal exists below
$L_\alpha (V_{\lambda +1})$
. Such an ordinal exists below
![]() $\Theta $
because all the subsets of
$\Theta $
because all the subsets of
![]() $V_{\lambda +1}$
in
$V_{\lambda +1}$
in
![]() $L(V_{\lambda +1})$
are elements of
$L(V_{\lambda +1})$
are elements of
![]() $L_\Theta (V_{\lambda +1})$
(see, for example, [Reference Dimonte3, Lemma 5.6]). In addition, we define
$L_\Theta (V_{\lambda +1})$
(see, for example, [Reference Dimonte3, Lemma 5.6]). In addition, we define
![]() $\alpha _y=0$
for all
$\alpha _y=0$
for all
![]() $y \in V_{\lambda +1}$
with the property that (7) fails in
$y \in V_{\lambda +1}$
with the property that (7) fails in
![]() $L(V_{\lambda +1})$
. The resulting function
$L(V_{\lambda +1})$
. The resulting function
![]() $y\mapsto \alpha _y$
is then definable in
$y\mapsto \alpha _y$
is then definable in
![]() $L(V_{\lambda +1})$
. We now want to prove that
$L(V_{\lambda +1})$
. We now want to prove that
For any
![]() $x \in V_{\lambda +1}$
, we define
$x \in V_{\lambda +1}$
, we define
![]() $<_x$
to be the canonical well-ordering of
$<_x$
to be the canonical well-ordering of
![]() $HOD^{L(V_{\lambda +1})}_{x}$
, the inner model of all sets hereditarily definable in
$HOD^{L(V_{\lambda +1})}_{x}$
, the inner model of all sets hereditarily definable in
![]() $L(V_{\lambda +1})$
with ordinals and x as parameters.Footnote
7
In addition, for all
$L(V_{\lambda +1})$
with ordinals and x as parameters.Footnote
7
In addition, for all
![]() $x,y\in V_{\lambda +1}$
, we let
$x,y\in V_{\lambda +1}$
, we let
![]() $g_x(y)$
denote the
$g_x(y)$
denote the
![]() $<_x$
-smallest surjection from
$<_x$
-smallest surjection from
![]() $V_{\lambda +1}$
to
$V_{\lambda +1}$
to
![]() $\alpha _y$
, if it exists and otherwise
$\alpha _y$
, if it exists and otherwise
![]() $g_x(y)=0$
. The map
$g_x(y)=0$
. The map
![]() $x \mapsto g_x$
is also definable in
$x \mapsto g_x$
is also definable in
![]() $L(V_{\lambda +1})$
. It is now easy to see that the function f defined by
$L(V_{\lambda +1})$
. It is now easy to see that the function f defined by
 $$ \begin{align*}f(x,y,z)= \begin{cases} g_x(y)(z), & \text{if } g_x(y)\neq 0\\ 0, & \text{otherwise} \end{cases} \end{align*} $$
$$ \begin{align*}f(x,y,z)= \begin{cases} g_x(y)(z), & \text{if } g_x(y)\neq 0\\ 0, & \text{otherwise} \end{cases} \end{align*} $$
is a surjection from
![]() $V_{\lambda +1}^3$
to
$V_{\lambda +1}^3$
to
![]() $\alpha $
and hence
$\alpha $
and hence
![]() $\alpha <\Theta $
.
$\alpha <\Theta $
.
In particular, we know that (7) holds in
![]() $L_\alpha (V_{\lambda +1})$
for all
$L_\alpha (V_{\lambda +1})$
for all
![]() $y \in M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1}$
. By the fact that the sequence of good ordinals is cofinal in
$y \in M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1}$
. By the fact that the sequence of good ordinals is cofinal in
![]() $\Theta $
and that the
$\Theta $
and that the
![]() $\vec {\mathcal {F}}$
-Baire property is upward absolute, we can assume that
$\vec {\mathcal {F}}$
-Baire property is upward absolute, we can assume that
![]() $\alpha $
is good. Then, by Theorem 4.13, there exist
$\alpha $
is good. Then, by Theorem 4.13, there exist
![]() $\bar \alpha <\lambda $
and an elementary embedding
$\bar \alpha <\lambda $
and an elementary embedding
such that
![]() $\pi \!\restriction \! (M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1})=\text {id}_{M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1}}$
. Thus, we can conclude that
$\pi \!\restriction \! (M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1})=\text {id}_{M_{\omega }[\vec {\lambda }] \cap V_{\lambda +1}}$
. Thus, we can conclude that
 $$ \begin{align*} & \forall y\in M_{\omega}[\vec{\lambda}] \cap V_{\lambda+1} ~ L_{\alpha}(V_{\lambda+1}) \models {\text{"}{{X_{\varphi,y}\ has\ the\ \vec{\mathcal{F}}\text{-}Baire\ property}}\text{"}} \\ \Longleftrightarrow ~ {} ~ & \forall y\in M_{\omega}[\vec{\lambda}] \cap V_{\lambda+1} ~L_{\bar \alpha}(M_{\omega}[\vec{\lambda}] \cap V_{\lambda+1}) \models {\text{"}{{X_{\varphi,y}\ has\ the\ \vec{\mathcal{F}}\text{-}Baire\ property}}\text{"}} \\ \Longleftrightarrow ~ {} ~& L_{\bar \alpha}(M_{\omega}[\vec{\lambda}] \cap V_{\lambda+1}) \models \forall y \in V_{\lambda+1} ~ {\text{"}{{X_{\varphi,y}\ has\ the\ \vec{\mathcal{F}}\text{-}Baire\ property}}\text{"}} \\ \Longleftrightarrow ~ {} ~ & L_{\alpha}(V_{\lambda+1}) \models \forall y \in V_{\lambda+1} ~ {\text{"}{{X_{\varphi,y}\ has\ the\ \vec{\mathcal{F}}\text{-}Baire\ property}}\text{"}}. \end{align*} $$
$$ \begin{align*} & \forall y\in M_{\omega}[\vec{\lambda}] \cap V_{\lambda+1} ~ L_{\alpha}(V_{\lambda+1}) \models {\text{"}{{X_{\varphi,y}\ has\ the\ \vec{\mathcal{F}}\text{-}Baire\ property}}\text{"}} \\ \Longleftrightarrow ~ {} ~ & \forall y\in M_{\omega}[\vec{\lambda}] \cap V_{\lambda+1} ~L_{\bar \alpha}(M_{\omega}[\vec{\lambda}] \cap V_{\lambda+1}) \models {\text{"}{{X_{\varphi,y}\ has\ the\ \vec{\mathcal{F}}\text{-}Baire\ property}}\text{"}} \\ \Longleftrightarrow ~ {} ~& L_{\bar \alpha}(M_{\omega}[\vec{\lambda}] \cap V_{\lambda+1}) \models \forall y \in V_{\lambda+1} ~ {\text{"}{{X_{\varphi,y}\ has\ the\ \vec{\mathcal{F}}\text{-}Baire\ property}}\text{"}} \\ \Longleftrightarrow ~ {} ~ & L_{\alpha}(V_{\lambda+1}) \models \forall y \in V_{\lambda+1} ~ {\text{"}{{X_{\varphi,y}\ has\ the\ \vec{\mathcal{F}}\text{-}Baire\ property}}\text{"}}. \end{align*} $$
These computation show that every set of the form
![]() $X_{\varphi ,y}$
with
$X_{\varphi ,y}$
with
![]() $y\in V_{\lambda +1}$
has the
$y\in V_{\lambda +1}$
has the
![]() $\vec {\mathcal {F}}$
-Baire property.
$\vec {\mathcal {F}}$
-Baire property.
5 Open questions
We close this paper by stating two questions raised by the above results. As mentioned in the introduction, our results suggest that large cardinals assumptions can be studied through the provable validity of Perfect Set Theorems for simply definable sets at singular cardinals of countable cofinality. In particular, our results suggest that the existence of an I2-embedding with critical sequence
![]() $\vec {\lambda }$
naturally corresponds to the validity of a Perfect Set Theorem for subsets of
$\vec {\lambda }$
naturally corresponds to the validity of a Perfect Set Theorem for subsets of
![]() $C(\vec {\lambda })$
that are definable by
$C(\vec {\lambda })$
that are definable by
![]() $\Sigma _1$
-formulas with parameters in
$\Sigma _1$
-formulas with parameters in
![]() $V_\lambda \cup \{\vec {\lambda }\}$
, where
$V_\lambda \cup \{\vec {\lambda }\}$
, where
![]() $\lambda $
is the supremum of the sequence
$\lambda $
is the supremum of the sequence
![]() $\vec {\lambda }$
. We therefore ask if the conclusion of Theorem 1.4 can also be derived from substantially weaker large cardinal assumptions:
$\vec {\lambda }$
. We therefore ask if the conclusion of Theorem 1.4 can also be derived from substantially weaker large cardinal assumptions:
Question 5.1. Let
![]() $\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of cardinals with supremum
$\vec {\lambda }=\langle {\lambda _n}~\vert ~{n<\omega }\rangle $
be a strictly increasing sequence of cardinals with supremum
![]() $\lambda $
such that
$\lambda $
such that
![]() $\lambda _n$
is a
$\lambda _n$
is a
![]() ${<}\lambda $
-supercompact cardinal for all
${<}\lambda $
-supercompact cardinal for all
![]() $n<\omega $
. If X is a subset of
$n<\omega $
. If X is a subset of
![]() ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
![]() $\lambda $
that is definable by a
$\lambda $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $V_\lambda \cup \{\vec {\lambda }\}$
, is there a perfect embedding
$V_\lambda \cup \{\vec {\lambda }\}$
, is there a perfect embedding
![]() ${\iota }:{{}^\omega \lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
${\iota }:{{}^\omega \lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
![]() ${\mathrm {{ran}}(\iota )}\subseteq X$
? If yes, what about subsets of
${\mathrm {{ran}}(\iota )}\subseteq X$
? If yes, what about subsets of
![]() ${\mathcal {P}}({\lambda })$
that are definable by
${\mathcal {P}}({\lambda })$
that are definable by
![]() $\Sigma _1$
-formulas with parameters in
$\Sigma _1$
-formulas with parameters in
![]() $V_\lambda \cup \{V_\lambda ,\vec {\lambda }\}$
?
$V_\lambda \cup \{V_\lambda ,\vec {\lambda }\}$
?
In another direction, we also ask which large cardinal assumptions are necessary to overcome the limitations to the influence of I2-embeddings given by Theorem 1.5. Note that, by Theorem 1.1, an I0-embedding suffices for this task. Remember that an I1-embedding is a non-trivial elementary embedding
![]() ${j}:{V_{\lambda +1}}\longrightarrow {V_{\lambda +1}}$
.
${j}:{V_{\lambda +1}}\longrightarrow {V_{\lambda +1}}$
.
Question 5.2. Let
![]() ${j}:{V_{\lambda +1}}\longrightarrow {V_{\lambda +1}}$
be an I1-embedding. If X is a subset of
${j}:{V_{\lambda +1}}\longrightarrow {V_{\lambda +1}}$
be an I1-embedding. If X is a subset of
![]() ${\mathcal {P}}({\lambda })$
of cardinality greater than
${\mathcal {P}}({\lambda })$
of cardinality greater than
![]() $\lambda $
that is definable by a
$\lambda $
that is definable by a
![]() $\Sigma _1$
-formula with parameters in
$\Sigma _1$
-formula with parameters in
![]() $V_{\lambda +1}$
, is there a perfect embedding
$V_{\lambda +1}$
, is there a perfect embedding
![]() ${\iota }:{{}^\omega \lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
${\iota }:{{}^\omega \lambda }\longrightarrow {{\mathcal {P}}({\lambda })}$
with
![]() ${\mathrm {{ran}}(\iota )}\subseteq X$
? If yes, what about subsets of
${\mathrm {{ran}}(\iota )}\subseteq X$
? If yes, what about subsets of
![]() ${\mathcal {P}}({\lambda })$
that are definable over
${\mathcal {P}}({\lambda })$
that are definable over
![]() $V_\lambda $
by
$V_\lambda $
by
![]() $\Sigma ^1_n$
-formulas with parameters in
$\Sigma ^1_n$
-formulas with parameters in
![]() $V_{\lambda +1}$
?
$V_{\lambda +1}$
?
Acknowledgments
The authors are thankful to the anonymous referees for the careful reading of the manuscript and several helpful comments.
Funding
The first and second author partially supported by the Italian PRIN 2017 Grant “Mathematical Logic: models, sets, computability”, the first author is further partially supported by the Italian PRIN 2022 Grant “Models, Sets and Classifications”. The third author gratefully acknowledges support from the Deutsche Forschungsgemeinschaft (Project number 522490605) and the Spanish Government under grant EUR2022-134032.