Article contents
Degrees of Structures1
Published online by Cambridge University Press: 12 March 2014
Extract
Consider those structures that consist of a countable universe and a finite number of predicates and functions. Let 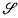 = ‹∣
= ‹∣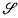 ∣, P1, …, Pn, f1, …, fm› be such a structure. We will restrict our consideration to structures,
∣, P1, …, Pn, f1, …, fm› be such a structure. We will restrict our consideration to structures, 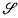 , whose universe, ∣
, whose universe, ∣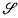 ∣, is a set of natural numbers, and thus we will be able to apply the notions of recursion theory to structures. Using deg(S) to refer to the degree of unsolvability of a set S, we can assign a degree of unsolvability to the structure
∣, is a set of natural numbers, and thus we will be able to apply the notions of recursion theory to structures. Using deg(S) to refer to the degree of unsolvability of a set S, we can assign a degree of unsolvability to the structure 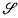 by defining deg(
by defining deg(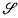 ) to be the least upper bound of the degrees of the universe, predicates, and functions of
) to be the least upper bound of the degrees of the universe, predicates, and functions of 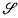 . If we view
. If we view 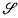 as a presentation of the class of all structures which are isomorphic to
as a presentation of the class of all structures which are isomorphic to 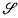 (in the usual sense), then the deg(
(in the usual sense), then the deg(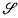 ) can be called the degree of the presentation
) can be called the degree of the presentation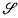 .
.
While deg(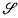 ) is a natural degree to assign to the structure
) is a natural degree to assign to the structure 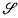 , it is not the only possibility. Indeed since a structure
, it is not the only possibility. Indeed since a structure 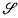 may have isomorphic presentations with different degrees, deg(
may have isomorphic presentations with different degrees, deg(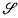 ) has the deficiency of not being isomorphically invariant. We can assign degrees to some (but not all) structures
) has the deficiency of not being isomorphically invariant. We can assign degrees to some (but not all) structures 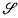 in an isomorphically invariant fashion by looking at the class of the degrees of all presentations isomorphic to
in an isomorphically invariant fashion by looking at the class of the degrees of all presentations isomorphic to 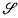 . If this class of degrees has a least element, we define it to be the degree of the isomorphism class of
. If this class of degrees has a least element, we define it to be the degree of the isomorphism class of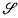 which we write deg([
which we write deg([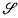 ]).
]).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
Footnotes
The results in this paper are taken from the author's Ph.D. thesis (University of Illinois at Urbana-Champaign) which was written with the valuable guidance of Professor Carl G. Jockusch.
References
REFERENCES
- 83
- Cited by


