Article contents
Degrees of recursively enumerable topological spaces
Published online by Cambridge University Press: 12 March 2014
Extract
In [5], Metakides and Nerode introduced the study of recursively enumerable (r.e.) substructures of a recursively presented structure. The main line of study presented in [5] is to examine the effective content of certain algebraic structures. In [6], Metakides and Nerode studied the lattice of r.e. subspaces of a recursively presented vector space. This lattice was later studied by Kalantari, Remmel, Retzlaff and Shore. Similar studies have been done by Metakides and Nerode [7] for algebraically closed fields, by Remmel [10] for Boolean algebras and by Metakides and Remmel [8] and [9] for orderings. Kalantari and Retzlaff [4] introduced and studied the lattice of r.e. subsets of a recursively presented topological space. Kalantari and Retzlaff considered X, a topological space with ⊿, a countable basis. This basis is coded into integers and with the help of this coding, r.e. subsets of ω give rise to r.e. subsets of X. The notion of “recursiveness” of a topological space is the natural next step which gives rise to the question of what should be the “degree” of an r.e. open subset of X? It turns out that any r.e. open set partitions ⊿; into four sets whose Turing degrees become central in answering the question raised above.
In this paper we show that the degrees of the elements of the partition of ⊿ imposed by an r.e. open set can be “controlled independently” in a sense to be made precise in the body of the paper. In [4], Kalantari and Retzlaff showed that given A any r.e. set and 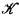 any r.e. open subset of X, there exists an r.e. open set ℋ which is a subset of
any r.e. open subset of X, there exists an r.e. open set ℋ which is a subset of 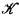 and is dense in
and is dense in 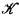 (in a topological sense) and in which A is coded. This shows that modulo a nowhere dense set, an r.e. open set can become as complicated as desired. After giving the general technical and notational machinery in §1, and giving the particulars of our needs in §2, in §3 we prove that the set ℋ described above could be made to be precisely of degree of A. We then go on and establish various results (both existential and universal) on the mentioned partitioning of ⊿. One of the surprising results is that there are r.e. open sets such that every element of partitioning of ⊿ is of a different degree. Since the exact wording of the results uses the technical definitions of these partitioning elements, we do not summarize the results here and ask the reader to examine §3 after browsing through §§1 and 2.
(in a topological sense) and in which A is coded. This shows that modulo a nowhere dense set, an r.e. open set can become as complicated as desired. After giving the general technical and notational machinery in §1, and giving the particulars of our needs in §2, in §3 we prove that the set ℋ described above could be made to be precisely of degree of A. We then go on and establish various results (both existential and universal) on the mentioned partitioning of ⊿. One of the surprising results is that there are r.e. open sets such that every element of partitioning of ⊿ is of a different degree. Since the exact wording of the results uses the technical definitions of these partitioning elements, we do not summarize the results here and ask the reader to examine §3 after browsing through §§1 and 2.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
References
REFERENCES
- 12
- Cited by


