Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T22:36:11.628Z Has data issue: false hasContentIssue false
  • English
  • Français

Degrees joining to 0′

Published online by Cambridge University Press:  12 March 2014

David B. Posner  and
Robert W. Robinson
David B. Posner
Affiliation:
San Jose State University, San Jose, California 95192
Robert W. Robinson
Affiliation:
University of Newcastle, New South Wales, Australia 2308
Get access Rights & Permissions [Opens in a new window]

Abstract

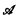It is shown that if and 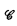are sets of degrees uniformly recursive in 0′ with 0 ∈ 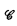then there is a degree b with b′ = 0′, b ∪ c = 0′ for every c ∈ 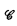, and a ≰ b for every a ∈ ˜ {0}. The proof is given as an oracle construction recursive in 0′. It follows that any nonrecursive degree below 0′ can be joined to 0′ by a degree strictly below 0′. Also, if a < 0′ and a″ = 0″ then there is a degree b such that a ∪ b = 0′ and a ∩ b = 0.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 46 , Issue 4 , December 1981 , pp. 714 - 722
Copyright
Copyright © Association for Symbolic Logic 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cooper, S. B., Minimal degrees and the jump operator, this Journal, vol. 38 (1973), pp. 249–271.Google Scholar
[2]Epstein, R. L., Minimal degrees of unsolvability and the full approximation construction, Memoirs of the American Mathematical Society, no. 162, American Mathematical Society, Providence, RI, 1975.Google Scholar
[3]Friedberg, R. M., A criterion for completeness of degrees of unsolvability, this Journal, vol. 22 (1957), pp. 159–160.Google Scholar
[4]Jockusch, C., Degrees in which the recursive sets are uniformly recursive, Canadian Journal of Mathematics, vol. 24 (1972), pp. 1092–1099.CrossRefGoogle Scholar
[5]Jockusch, C., Simple proofs of some theorems on high degrees, Canadian Journal of Mathematics, vol. 29 (1977), pp. 1072–1080.CrossRefGoogle Scholar
[6]Jockusch, C. and Posner, D., Double jumps of minimal degrees, this Journal, vol. 43 (1978), pp. 715–724.Google Scholar
[7]Miller, W. and Martin, D.A., The degrees of hyperimmune sets, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 159–166.CrossRefGoogle Scholar
[8]Posner, D., High degrees, Doctoral Dissertation, University of California, Berkeley, 1977.Google Scholar
[9]Posner, D., The upper semilattice of degrees ≤ 0′ is complemented, this Journal, vol. 46 (1981), pp. 705–713.Google Scholar
[10]Robinson, R. W., Degrees joining to 0′, Notices of the American Mathematical Society, vol. 19 (1972), p. A–615.Google Scholar
[11]Sasso, L. P., A cornucopia of minimal degrees, this Journal, vol. 39 (1974), pp. 571–574.Google Scholar
[12]Shoenfield, J. R., A theorem on minimal degrees, this Journal, vol. 31 (1966), pp. 539–544.Google Scholar
[13]Shoenfield, J. R., Degrees of unsolvability, North-Holland, Amsterdam, 1971.Google Scholar
[14]Yates, C. E. M., Recursively enumerable degrees and the degrees less than 0′, Sets, models and recursion theory (Crossley, J. N., Editor), North-Holland, Amsterdam, 1967.Google Scholar