Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T12:56:01.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Degree invariance in the Π10classes

Published online by Cambridge University Press:  12 March 2014

Rebecca Weber
Rebecca Weber*
Affiliation:
Department of Mathematics, 6188 Kemeny Hall, Dartmouth College, Hanover, NH 03755, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let denote the collection of all Π10 classes, ordered by inclusion. A collection of Turing degrees in is called invariant over if there is some collection 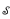of Π10 classes representing exactly the degrees such that is invariant under automorphisms of . Herein we expand the known degree invariant classes of , previously including only {0} and the array noncomputable degrees, to include all highn and non-lown degrees for n > 2. This is a corollary to a very general definability result. The result is carried out in a substructure G of , within which the techniques used model those used by Cholak and Harrington [6] to obtain the same definability for the c.e. sets. We work back and forth between G and to show that this definability in G gives the desired degree invariance over .

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 4 , December 2011 , pp. 1184 - 1210
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cenzer, D., Π10, classes in computability theory, Handbook of computability theory (Griffor, E. R., editor), Studies in Logic and the Foundations of Mathematics, vol. 140, North-Holland, Amsterdam, 1999, pp. 37–85.CrossRefGoogle Scholar
[2]Cenzer, D. and Jockusch, C. G. Jr., Π10 classes—structure and applications, Computability theory audits applications (Boulder, CO, 1999), Contemporary Mathematics, vol. 257, American Mathematical Society, Providence, RI, 2000, pp. 39–59.Google Scholar
[3]Cenzer, D. and Nies, A., Global properties of the lattice of Π10 classes, Proceedings of the American Mathematical Society, vol. 132 (2004), pp. 239–249.CrossRefGoogle Scholar
[4]Cenzer, D. and Remmel, J. B., Π10 classes in mathematics, Handbook of recursive mathematics, Volume 2 (Ershov, Y. L., Goncharov, S. S., Nerode, A., and Remmel, J. B., editors), Studies in Logic and the Foundations of Mathematics, vol. 139, North-Holland, Amsterdam, 1998, pp. 623–821.Google Scholar
[5]Cholak, P. A., Coles, R., Downey, R. G., and Herrmann, E., Automorphisms of the lattice of Π10 classes: perfect thin classes and anc degrees, Transactions of the American Mathematical Society, vol. 353 (2001), no. 12, pp. 4899–4924, (electronic).CrossRefGoogle Scholar
[6]Cholak, P. A. and Harrington, L. A., On the definability of the double jump in the computably enumerable sets, Journal of Mathematical Logic, vol. 2 (2002), no. 2, pp. 261–296.CrossRefGoogle Scholar
[7]Downey, Rod, Undecidability of L(F∞) and other lattices of r.e. substructures, Annals of Pure and Applied Logic, vol. 32 (1986), no. 1, pp. 17–26.CrossRefGoogle Scholar
[8]Downey, Rod, Correction to: “Undecidability of L(F∞) and other lattices of r.e. substructures” in [7], Annals of Pure and Applied Logic, vol. 48 (1990), no. 3, pp. 299–301.CrossRefGoogle Scholar
[9]Harrington, L. A. and Soare, R. I., Definability, automorphisms, and dynamic properties of computably enumerable sets, The Bulletin of Symbolic Logic, vol. 2 (1996), no. 2, pp. 199–213.CrossRefGoogle Scholar
[10]Lachlan, A. H., Degrees of recursively enumerable sets which have no maximal supersets, this Journal, vol. 33 (1968), pp. 431–443.Google Scholar
[11]Lerman, M. and Soare, R. I., D-simple sets, small sets, and degree classes, Pacific Journal of Mathematics, vol. 87 (1980), no. 1, pp. 135–155.CrossRefGoogle Scholar
[12]Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für die Mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar
[13]Nerode, Anil and Remmel, Jeffrey, A survey of lattices of r.e. substructures, Recursion theory (Ithaca, N.Y., 1982), Proceedings of Symposia in Pure Mathematics, vol. 42, American Mathematical Society, Providence, RI, 1985, pp. 323–375.CrossRefGoogle Scholar
[14]Remmel, Jeffrey B., Recursion theory on algebraic structures with independent sets, Annals of Mathematical Logic, vol. 18 (1980), no. 2, pp. 153–191.CrossRefGoogle Scholar
[15]Schoenfield, J. R., Degrees of classes of recursively enumerable sets, this Journal, vol. 41 (1976), pp. 695–696.Google Scholar
[16]Soare, R. I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag, Heidelberg, 1987.CrossRefGoogle Scholar
[17]Weber, R., Invariance in and , Transactions of the American Mathematical Society, vol. 358 (2006), pp. 3023–3059.CrossRefGoogle Scholar