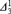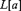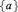Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2020.
On the ‘Definability of Definable’ Problem of Alfred Tarski.
Mathematics,
Vol. 8,
Issue. 12,
p.
2214.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2020.
Models of Set Theory in which Nonconstructible Reals First Appear at a Given Projective Level.
Mathematics,
Vol. 8,
Issue. 6,
p.
910.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2020.
On the
Δ
n
1
Problem of Harvey Friedman.
Mathematics,
Vol. 8,
Issue. 9,
p.
1477.
Enayat, Ali
Kanovei, Vladimir
and
Lyubetsky, Vassily
2021.
On Effectively Indiscernible Projective Sets and the Leibniz-Mycielski Axiom.
Mathematics,
Vol. 9,
Issue. 14,
p.
1670.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2021.
The full basis theorem does not imply analytic wellordering.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 4,
p.
102929.
Kanovei, V. G.
and
Lyubetsky, V. A.
2021.
Models of set theory in which the separation theorem fails.
Izvestiya: Mathematics,
Vol. 85,
Issue. 6,
p.
1181.
Kanovei, Vladimir Grigorevich
and
Lyubetskii, Vasilii Aleksandrovich
2021.
Модели теории множеств, в которых теорема отделимости неверна.
Известия Российской академии наук. Серия математическая,
Vol. 85,
Issue. 6,
p.
164.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2022.
On the ‘definability of definable’ problem of Alfred Tarski, Part II.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 12,
p.
8651.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2022.
A Model in Which Well-Orderings of the Reals Appear at a Given Projective Level.
Axioms,
Vol. 11,
Issue. 8,
p.
354.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2022.
A Model in Which the Separation Principle Holds for a Given Effective Projective Sigma-Class.
Axioms,
Vol. 11,
Issue. 3,
p.
122.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2023.
A Model in Which Well-Orderings of the Reals First Appear at a Given Projective Level, Part II.
Mathematics,
Vol. 11,
Issue. 11,
p.
2517.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2024.
A good lightface Δn1 well-ordering of the reals does not imply the existence of boldface Δn−11 well-orderings.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 6,
p.
103426.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2024.
On the Uniform Projection Problem in Descriptive Set Theory.
Axioms,
Vol. 14,
Issue. 1,
p.
13.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2025.
On the Uniform Projection and Covering Problems in Descriptive Set Theory Under the Axiom of Constructibility.
Mathematics,
Vol. 13,
Issue. 3,
p.
409.
Kanovei, Vladimir Grigorevich
and
Lyubetskii, Vasilii Aleksandrovich
2025.
Независимость схемы свертки в арифметике второго порядка
от счетного выбора без параметров.
Математические заметки,
Vol. 117,
Issue. 2,
p.
257.
Kanovei, Vladimir
and
Lyubetsky, Vassily
2025.
Parameterfree Comprehension Does Not Imply Full Comprehension in Second Order Peano Arithmetic.
Studia Logica,
Vol. 113,
Issue. 1,
p.
109.