Definable FN bases

Extract

This paper is a sequel to [4]. Our main concern here is to study the FN bases, which correspond to classical notions like heirs and definable extensions. We also attempt to characterize these notions in our context. This leads to the use of tools like ultrapower constructions.

We continue to work under the assumptions and using the notation of [4, §1]. For example, we require a sufficiently saturated model 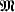of a fixed complete theory T in a language 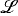, and ℒ and A and B are used to denote (not necessarily small) subsets of M. The concept of FN basis is defined in [4, Definition 3.2]. Nonforking is defined in [4, Definitions 2.2 and 3.7].

This paper is organized as follows: §1 deals with heirs and definability. The classical result stating that definability is equivalent to the uniqueness of an heir is generalized (Theorem 1.7). §2 uses an ultrapower to prove the existence of an heir (Corollary 2.6). We also determine exactly when embeddability into an ultrapower is possible. §3 relates ultrapowers to flatness and nonforking. In sharp contrast to the classical case, ultrapowers of FN bases need not be nonforking; but some criteria are established (Propositions 3.2 and 3.3, and Theorem 3.4). Finally, definability is characterized as the flatness of all ultrapowers (Theorem 3.6).