Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T21:43:13.739Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DEFINABILITY STRENGTH OF COMBINATORIAL PRINCIPLES

Published online by Cambridge University Press:  01 December 2016

WEI WANG
WEI WANG*
Affiliation:
INSTITUTE OF LOGIC AND COGNITION AND DEPARTMENT OF PHILOSOPHY SUN YAT-SEN UNIVERSITY, 135 XINGANG XI ROAD GUANGZHOU 510275, P.R. CHINAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the definability strength of combinatorial principles. In terms of definability strength, a combinatorial principle is strong if solving a corresponding combinatorial problem could help in simplifying the definition of a definable set. We prove that some consequences of Ramsey’s Theorem for colorings of pairs could help in simplifying the definitions of some 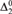${\rm{\Delta }}_2^0$ sets, while some others could not. We also investigate some consequences of Ramsey’s Theorem for colorings of longer tuples. These results of definability strength have some interesting consequences in reverse mathematics, including strengthening of known theorems in a more uniform way and also new theorems.

Keywords

03B3003F35reverse mathematicsdefinability strengthRamsey’s theoremfree setthin setrainbow Ramsey theorem
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 4 , December 2016 , pp. 1531 - 1554
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cholak, P. A., Giusto, M., Hirst, J. L., and Jockusch, C. G. Jr., Free sets and reverse mathematics , Reverse Mathematics 2001, Lecture Notes in Logic, vol. 21, Association for Symbolic Logic, La Jolla, CA, 2005, pp. 104–119.Google Scholar
[2] Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey’s theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
[3] Csima, B. and Mileti, J., The strength of the rainbow Ramsey theorem, this Journal, vol. 74 (2009), no. 4, pp. 1310–1324.Google Scholar
Dorais, F. G., Dzhafarov, D. D., Hirst, J. L., Mileti, J. R., and Shafer, P., On uniform relationships between combinatorial problems . Transactions of the American Mathematical Society, vol. 368 (2016), no. 2, pp. 1321–1359.Google Scholar
Downey, R. and Hirschfeldt, D., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Harizanov, V. S., Turing degrees of certain isomorphic images of computable relations . Annals of Pure and Applied Logic, vol. 93 (1998), no. 1–3, pp. 103–113.Google Scholar
Hirschfeldt, D. R., Slicing the Truth, Lecture Notes Series. Institute for Mathematical Sciences. National University of Singapore, vol. 28, World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2015.Google Scholar
[8] Hirschfeldt, D. R. and Shore, R. A., Combinatorial principles weaker than Ramsey’s theorem for pairs, this Journal, vol. 72 (2007), no. 1, pp. 171–206.Google Scholar
Hirschfeldt, D. R., Shore, R. A., and Slaman, T. A., The atomic model theorem and type omitting , Transactions of the American Mathematical Society, vol. 361 (2009), no. 11, pp. 5805–5837.Google Scholar
[10] Jockusch, C. G. Jr., Ramsey’s theorem and recursion theory, this Journal, vol. 37 (1972), no. 2, pp. 268–280.Google Scholar
Kang, X., Combinatorial principles between ${\rm{RRT}}_2^2$ and ${\rm{RT}}_2^2$ , preprint.Google Scholar
[12] Kurtz, S., Randomness and Genericty in the Degrees of Unsolvability , Ph.D thesis, University of Illinios at Urbana-Champaign, 1981.Google Scholar
Lerman, M., Solomon, R., and Towsner, H., Separating principles below Ramsey’s theorem for pairs . Journal of Mathematical Logic, vol. 13 (2013), no. 2, p. 1350007, 44.Google Scholar
Patey, L., Controlling iterated jumps of solutions to combinatorial problems, Computability , to appear.Google Scholar
[15] Patey, L., Somewhere over the rainbow Ramsey theorem for pairs, to appear, 2015.Google Scholar
Seetapun, D. and Slaman, T. A., On the strength of Ramsey’s theorem . Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 570–582.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Perspectives in Logic, second edition, Cambridge University Press, Cambridge; Association for Symbolic Logic, Poughkeepsie, NY, 2009.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Omega Series. Springer–Verlag, Heidelberg, 1987.Google Scholar
[19] Wang, W., Rainbow Ramsey Theorem for triples is strictly weaker than the Arithmetic Comprehension Axiom, this Journal, vol. 78 (2013), no. 3, 824–836.Google Scholar
Wang, W., Cohesive sets and rainbows . Annals of Pure and Applied Logic, vol. 165 (2014), no. 2, 389–408.Google Scholar
Wang, W., Some logically weak Ramseyan theorems . Advances in Mathematics, vol. 261 (2014), pp. 1–25.Google Scholar