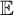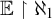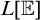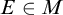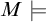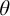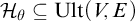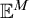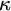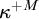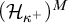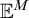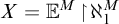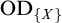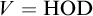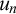1 Introduction
Let M be a premouse.Footnote
1
Write
![]() $\mathbb {E}^M$
for the extender sequence of M, not including the active extender
$\mathbb {E}^M$
for the extender sequence of M, not including the active extender
![]() $F^M$
of M. Write
$F^M$
of M. Write
![]() $\mathbb {E}_+^M=\mathbb {E}^M\ \widehat {\ }\ \left <F^M\right>$
. Write
$\mathbb {E}_+^M=\mathbb {E}^M\ \widehat {\ }\ \left <F^M\right>$
. Write
![]() $\left \lfloor M\right \rfloor $
for the universe of M. Write
$\left \lfloor M\right \rfloor $
for the universe of M. Write ![]() . Write
. Write
![]() $\mathrm {PS}$
for the Power Set Axiom.
$\mathrm {PS}$
for the Power Set Axiom.
We consider here the following questions:
-
– Given
 $E\in M$
such that
$E\in M$
such that
 $M\models $
“E is an extender”, is
$M\models $
“E is an extender”, is
 $E\in \mathbb {E}^M$
?
$E\in \mathbb {E}^M$
? -
– (Steel) Suppose
 $M\models \mathrm {ZFC}$
. Does
$M\models \mathrm {ZFC}$
. Does
 $M\models $
“There is
$M\models $
“There is
 $X\subseteq \aleph _1$
such that
$X\subseteq \aleph _1$
such that
 $V=\mathrm {HOD}_{\{X\}}$
”?
$V=\mathrm {HOD}_{\{X\}}$
”? -
– Is
 $\mathbb {E}^M$
definable over
$\mathbb {E}^M$
definable over
 $\left \lfloor M\right \rfloor $
, possibly from some (small) parameter?
$\left \lfloor M\right \rfloor $
, possibly from some (small) parameter?
Throughout the paper, when we write “
![]() $\mathbb {E}^M$
is definable (within some complexity class)”, we literally mean that the class
$\mathbb {E}^M$
is definable (within some complexity class)”, we literally mean that the class
![]() $\{\mathbb {E}^M\!\upharpoonright \!\alpha \mid \alpha <\mathrm {Ord}^M\}$
is so definable. Given a definability class
$\{\mathbb {E}^M\!\upharpoonright \!\alpha \mid \alpha <\mathrm {Ord}^M\}$
is so definable. Given a definability class
![]() $\Sigma $
, We write
$\Sigma $
, We write
![]() $\Sigma ^N(X)$
for the class of relations which are
$\Sigma ^N(X)$
for the class of relations which are
![]() $\Sigma $
-definable over the structure N from parameters in X, or just
$\Sigma $
-definable over the structure N from parameters in X, or just
![]() $\Sigma ^N$
for
$\Sigma ^N$
for
![]() $\Sigma ^N(\emptyset )$
. As usual,
$\Sigma ^N(\emptyset )$
. As usual,
![]() $\Delta _n^N(X)$
denotes
$\Delta _n^N(X)$
denotes
![]() $\Sigma _n^N(X)\cap \Pi ^N_n(X)$
.
$\Sigma _n^N(X)\cap \Pi ^N_n(X)$
.
Answers to certain instances of the above questions have been known for some time. Kunen proved that
![]() $L[U]$
satisfies “U is the unique normal measure”, and therefore satisfies “
$L[U]$
satisfies “U is the unique normal measure”, and therefore satisfies “
![]() $V=\mathrm {HOD}$
”. Recall that
$V=\mathrm {HOD}$
”. Recall that
![]() $M_n$
is the minimal proper class mouse with n Woodin cardinals. Steel proved [Reference Schindler5] that for
$M_n$
is the minimal proper class mouse with n Woodin cardinals. Steel proved [Reference Schindler5] that for
![]() $n\leq \omega $
,
$n\leq \omega $
,
![]() $\mathbb {E}^{M_n}$
is definable over
$\mathbb {E}^{M_n}$
is definable over
![]() $\left \lfloor M_n\right \rfloor $
without parameters.Footnote
2
The author proved similar results for larger, sufficiently self-iterable mice in [Reference Schlutzenberg6] and [Reference Schlutzenberg11]. The proofs of these earlier results depended on the mice in question being sufficiently self-iterable. But non-meek mice typically fail to have such self-iterability, making it difficult to generalize these kinds of arguments to models with higher large cardinals.
$\left \lfloor M_n\right \rfloor $
without parameters.Footnote
2
The author proved similar results for larger, sufficiently self-iterable mice in [Reference Schlutzenberg6] and [Reference Schlutzenberg11]. The proofs of these earlier results depended on the mice in question being sufficiently self-iterable. But non-meek mice typically fail to have such self-iterability, making it difficult to generalize these kinds of arguments to models with higher large cardinals.
The main result of the paper is the following, Theorem 1.1. It answers Steel’s question above positively, in fact with ![]() .Footnote
3
.Footnote
3
Theorem 1.1. Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse satisfying
$(0,\omega _1+1)$
-iterable premouse satisfying
![]() $\mathrm {PS}$
and
$\mathrm {PS}$
and ![]() . Then
. Then
Therefore if
![]() $\left \lfloor M\right \rfloor \models \mathrm {ZFC}$
then
$\left \lfloor M\right \rfloor \models \mathrm {ZFC}$
then
![]() $\left \lfloor M\right \rfloor \models $
“
$\left \lfloor M\right \rfloor \models $
“![]() ” and
” and
![]() $M\models \mathrm {ZFC}$
.Footnote
4
$M\models \mathrm {ZFC}$
.Footnote
4
Note that the only large cardinal restriction on the mice involved is the paper’s global assumption that all premice considered have only short extenders on their sequence. This means that we need to deal with mice which are significantly non-self-iterable, for which the earlier arguments mentioned above do not seem to apply.
For the proof, we will use a method which avoids any self-iterability, and is more focused on condensation properties. The first proof we give, in Section 3, will actually yield a more general and local version, in which the mouse can have a largest cardinal, but in which case we must allow somewhat higher complexity in the definition of
![]() $\mathbb {E}^M$
from the parameter
$\mathbb {E}^M$
from the parameter ![]() . We will also give a variant proof in Section 4, which uses the same main idea, but is a little simpler. (However, it does not give all of the information provided by the first proof.) The argument in Section 3 was discovered in 2015, and that in Section 4 in 2019. The argument in Section 4 is used in the preprint [Reference Sargsyan, Schindler and Schlutzenberg2].
. We will also give a variant proof in Section 4, which uses the same main idea, but is a little simpler. (However, it does not give all of the information provided by the first proof.) The argument in Section 3 was discovered in 2015, and that in Section 4 in 2019. The argument in Section 4 is used in the preprint [Reference Sargsyan, Schindler and Schlutzenberg2].
We easily get the following corollary, which does involve some self-iterability:
Corollary 3.15.
Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse. Suppose M satisfies
$(0,\omega _1+1)$
-iterable premouse. Suppose M satisfies
![]() $\mathrm {PS}+$
“
$\mathrm {PS}+$
“![]() is
is
![]() $(\omega ,\omega _1+1)$
-iterable”. Then
$(\omega ,\omega _1+1)$
-iterable”. Then
![]() $\mathbb {E}^M$
is (lightface)
$\mathbb {E}^M$
is (lightface)
![]() $\Delta _2^{\left \lfloor M\right \rfloor }$
-definable and
$\Delta _2^{\left \lfloor M\right \rfloor }$
-definable and
![]() $\left \lfloor M\right \rfloor \models $
“Every set is
$\left \lfloor M\right \rfloor \models $
“Every set is
![]() $\mathrm {OD}$
”.Footnote
5
$\mathrm {OD}$
”.Footnote
5
To prove the more local version of Theorem 1.1 we will use certain extender maximality properties of
![]() $\mathbb {E}^M$
, Theorems 1.2 and 1.4, which are refinements of results from [Reference Schlutzenberg6], with similar proofs.
$\mathbb {E}^M$
, Theorems 1.2 and 1.4, which are refinements of results from [Reference Schlutzenberg6], with similar proofs.
Theorem 1.2 (Steel, Schlutzenberg).
Let M be an
![]() $(0,\omega _1+1)$
-iterable premouse. Let
$(0,\omega _1+1)$
-iterable premouse. Let
![]() $E\in M$
be such that
$E\in M$
be such that
![]() $M\models $
“E is a short, total, countably complete extender”,
$M\models $
“E is a short, total, countably complete extender”,
![]() $\nu _E$
is a cardinal of M and
$\nu _E$
is a cardinal of M and
![]() $\mathcal {H}_{\nu _E}^M\subseteq \mathrm {Ult}(M,E)$
. Then (the trivial completion of) E is in
$\mathcal {H}_{\nu _E}^M\subseteq \mathrm {Ult}(M,E)$
. Then (the trivial completion of) E is in
![]() $\mathbb {E}^M$
.
$\mathbb {E}^M$
.
Remark 1.3. Steel first proved that
![]() $E\in \mathbb {E}^M$
under the assumptions of 1.2 together with the added assumptions that
$E\in \mathbb {E}^M$
under the assumptions of 1.2 together with the added assumptions that
![]() $M\models \mathrm {PS}$
+ “
$M\models \mathrm {PS}$
+ “
![]() $\nu _E$
is regular” and
$\nu _E$
is regular” and
![]() $\mathrm {Ult}(M,E)|\nu _E=M|\nu _E$
. The author then generalized Steel’s proof to obtain 1.2.
$\mathrm {Ult}(M,E)|\nu _E=M|\nu _E$
. The author then generalized Steel’s proof to obtain 1.2.
Recall that if
![]() $M\models $
“E is a normal measure” then
$M\models $
“E is a normal measure” then
![]() $\nu _E=\mathrm {cr}(E)^{+M}$
, so the requirement that
$\nu _E=\mathrm {cr}(E)^{+M}$
, so the requirement that
![]() $\mathcal {H}_{\nu _E}^M\subseteq \mathrm {Ult}(M,E)$
holds automatically, and therefore
$\mathcal {H}_{\nu _E}^M\subseteq \mathrm {Ult}(M,E)$
holds automatically, and therefore
![]() $E\in \mathbb {E}^M$
(given M is iterable).
$E\in \mathbb {E}^M$
(given M is iterable).
Theorem 1.4. Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse. Let
$(0,\omega _1+1)$
-iterable premouse. Let
![]() $E,R\in M$
and
$E,R\in M$
and
![]() ${\tau \in \mathrm {Ord}^M}$
be such that
${\tau \in \mathrm {Ord}^M}$
be such that
![]() $\tau $
is a cardinal of M, R is a premouse,
$\tau $
is a cardinal of M, R is a premouse,
![]() $\rho _\omega ^R=\tau $
and
$\rho _\omega ^R=\tau $
and
![]() $M\models $
“E is a short extender,
$M\models $
“E is a short extender,
![]() $\mathcal {H}_\tau \subseteq \mathrm {Ult}(M,E)$
and
$\mathcal {H}_\tau \subseteq \mathrm {Ult}(M,E)$
and
![]() $R\triangleleft \mathrm {Ult}(M,E)$
”. Then
$R\triangleleft \mathrm {Ult}(M,E)$
”. Then
![]() $R\triangleleft M$
.
$R\triangleleft M$
.
Slightly less general versions of 1.2 and 1.4 were obtained by the author in 2006 [Reference Schlutzenberg6]. Prior to this, Woodin had conjectured that if M is a mouse,
![]() $\kappa $
is uncountable in M and
$\kappa $
is uncountable in M and
![]() $\kappa ^{+M}<\mathrm {Ord}^M$
, then
$\kappa ^{+M}<\mathrm {Ord}^M$
, then
![]() $L(\mathcal {P}(\kappa )^M)\models \mathrm {AC}$
. Woodin’s conjecture follows immediately from the following corollary (1.5) to the preceding theorems. Steel noticed that 1.5 follows from 1.4 combined with an argument of Woodin’s.Footnote
6
$L(\mathcal {P}(\kappa )^M)\models \mathrm {AC}$
. Woodin’s conjecture follows immediately from the following corollary (1.5) to the preceding theorems. Steel noticed that 1.5 follows from 1.4 combined with an argument of Woodin’s.Footnote
6
Corollary 1.5. Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse and
$(0,\omega _1+1)$
-iterable premouse and
![]() $\kappa \in \mathrm {Ord}^M$
be such that
$\kappa \in \mathrm {Ord}^M$
be such that
![]() $M\models $
“
$M\models $
“
![]() $\kappa $
is uncountable” and
$\kappa $
is uncountable” and
![]() $\kappa ^{+M}<\mathrm {Ord}^M$
. Then
$\kappa ^{+M}<\mathrm {Ord}^M$
. Then
![]() $M|\kappa ^{+M}$
is definable from parameters over
$M|\kappa ^{+M}$
is definable from parameters over
![]() $\mathcal {H}_{\kappa ^{+M}}^M$
.
$\mathcal {H}_{\kappa ^{+M}}^M$
.
In Section 5 we also describe a simplification to Mitchell–Steel fine structure of [Reference Mitchell and Steel1], making do without the parameters
![]() $u_n$
. One could just use the standard fine structure, but the simplification removes some complications, and we will officially make use of it throughout the paper.
$u_n$
. One could just use the standard fine structure, but the simplification removes some complications, and we will officially make use of it throughout the paper.
1.1 Conventions and notation
Note that some notation was introduced on page 1.
Most non-standard conventions are as in [Reference Schlutzenberg9, Section 1.1] or [Reference Schlutzenberg10, Section 1.1] (and mostly, but not completely, as in [Reference Schlutzenberg11, Section 1.1]). In particular, premice M have Mitchell–Steel indexing, except that we allow extenders of superstrong type in the extender sequence
![]() $\mathbb {E}_+^M$
(see [Reference Schlutzenberg9, Sections 1.1.2 and 1.1.6], [Reference Schlutzenberg and Trang12, Section 2]), and we adopt a simplified version of the Mitchell–Steel fine structure of [Reference Mitchell and Steel1], which avoids the parameters
$\mathbb {E}_+^M$
(see [Reference Schlutzenberg9, Sections 1.1.2 and 1.1.6], [Reference Schlutzenberg and Trang12, Section 2]), and we adopt a simplified version of the Mitchell–Steel fine structure of [Reference Mitchell and Steel1], which avoids the parameters
![]() $u_n$
, as explained in Section 5. By 5.8, this change actually has no impact on the fine structural notions such as standard parameters, k-soundness, etc. In Sections 1–4, when we write
$u_n$
, as explained in Section 5. By 5.8, this change actually has no impact on the fine structural notions such as standard parameters, k-soundness, etc. In Sections 1–4, when we write
![]() $p_k$
(the kth standard parameter), we mean the object defined as
$p_k$
(the kth standard parameter), we mean the object defined as
![]() $q_k$
in Section 5, as opposed to what is defined as
$q_k$
in Section 5, as opposed to what is defined as
![]() $p_k$
in Section 5. Moreover, we drop the “q-” from the fine structure terminology introduced in Section 5. Because of the change, we use the notation
$p_k$
in Section 5. Moreover, we drop the “q-” from the fine structure terminology introduced in Section 5. Because of the change, we use the notation
![]() $\mathrm {Hull}_{k+1}^M(X)$
and
$\mathrm {Hull}_{k+1}^M(X)$
and
![]() $\mathrm {cHull}_{k+1}^M(X)$
as defined in 5.1, not as in [Reference Schlutzenberg11].
$\mathrm {cHull}_{k+1}^M(X)$
as defined in 5.1, not as in [Reference Schlutzenberg11].
For a structure M,
![]() $\left \lfloor M\right \rfloor $
denotes the universe of M, and
$\left \lfloor M\right \rfloor $
denotes the universe of M, and
![]() $\mathcal {J}(M)$
denotes the rudimentary closure of
$\mathcal {J}(M)$
denotes the rudimentary closure of
![]() $M\cup \{M\}$
.
$M\cup \{M\}$
.
Let N be a premouse,
![]() $\mathbb {E}=\mathbb {E}^N$
and
$\mathbb {E}=\mathbb {E}^N$
and
![]() $\mathbb {E}_+=\mathbb {E}_+^N$
. Given
$\mathbb {E}_+=\mathbb {E}_+^N$
. Given
![]() $\alpha \leq \mathrm {Ord}^N$
, we write
$\alpha \leq \mathrm {Ord}^N$
, we write
![]() $N|\alpha =(\mathcal {J}_\alpha ^{\mathbb {E}},\mathbb {E}\!\upharpoonright \!\alpha ,\mathbb {E}_+(\alpha ))$
for the initial segment of N of ordinal height
$N|\alpha =(\mathcal {J}_\alpha ^{\mathbb {E}},\mathbb {E}\!\upharpoonright \!\alpha ,\mathbb {E}_+(\alpha ))$
for the initial segment of N of ordinal height
![]() $\alpha $
, including its active extender
$\alpha $
, including its active extender
![]() $\mathbb {E}_+(\alpha )$
, and
$\mathbb {E}_+(\alpha )$
, and
![]() $N||\alpha $
for its passivization
$N||\alpha $
for its passivization
![]() $(\mathcal {J}_\alpha ^{\mathbb {E}},\mathbb {E}\!\upharpoonright \!\alpha ,\emptyset )$
. If N is passive, then working inside N,
$(\mathcal {J}_\alpha ^{\mathbb {E}},\mathbb {E}\!\upharpoonright \!\alpha ,\emptyset )$
. If N is passive, then working inside N,
![]() $\mathcal {J}^{\mathbb {E}}$
also denotes N. We write
$\mathcal {J}^{\mathbb {E}}$
also denotes N. We write
![]() $\mathbb {e}^N=\mathbb {E}\!\upharpoonright \!\omega _1^N$
and
$\mathbb {e}^N=\mathbb {E}\!\upharpoonright \!\omega _1^N$
and ![]() .
.
Let
![]() $n<\omega $
. We say that N satisfies
$n<\omega $
. We say that N satisfies
![]() $(n+1)$
-condensation iff N is n-sound and whenever H is
$(n+1)$
-condensation iff N is n-sound and whenever H is
![]() $(n+1)$
-sound and
$(n+1)$
-sound and
![]() $\pi :H\to N$
is n-lifting (see [Reference Schlutzenberg9, Definition 2.1]) and
$\pi :H\to N$
is n-lifting (see [Reference Schlutzenberg9, Definition 2.1]) and
![]() $\rho _{n+1}^H\leq \mathrm {cr}(\pi )$
, then either
$\rho _{n+1}^H\leq \mathrm {cr}(\pi )$
, then either
![]() $H=\mathfrak {C}_{n+1}(N)$
or
$H=\mathfrak {C}_{n+1}(N)$
or
![]() $H\triangleleft N$
or, letting
$H\triangleleft N$
or, letting
![]() $\rho =\rho _{n+1}^H$
,
$\rho =\rho _{n+1}^H$
,
![]() $N|\rho $
is active with extender E and
$N|\rho $
is active with extender E and
![]() $H\triangleleft \mathrm {Ult}(N|\rho ,E)$
(see [Reference Schlutzenberg9, Theorem 5.2]). We say N satisfies
$H\triangleleft \mathrm {Ult}(N|\rho ,E)$
(see [Reference Schlutzenberg9, Theorem 5.2]). We say N satisfies
![]() $\omega $
-condensation iff it satisfies
$\omega $
-condensation iff it satisfies
![]() $(n+1)$
-condensation for all
$(n+1)$
-condensation for all
![]() $n<\omega $
.
$n<\omega $
.
Regarding (generalized) solidity, see Definition 2.1 and [Reference Schlutzenberg9, Section 1.1.3].
We say that N is an
![]() $\omega $
-premouse iff N is
$\omega $
-premouse iff N is
![]() $\omega $
-sound and
$\omega $
-sound and
![]() $\rho _\omega ^N=\omega $
; in this case we let
$\rho _\omega ^N=\omega $
; in this case we let
![]() $\deg (N)$
denote the least n such that
$\deg (N)$
denote the least n such that
![]() $\rho _{n+1}^N=\omega $
. An
$\rho _{n+1}^N=\omega $
. An
![]() $\omega $
-mouse is an
$\omega $
-mouse is an
![]() $(\omega ,\omega _1+1)$
-iterable
$(\omega ,\omega _1+1)$
-iterable
![]() $\omega $
-premouse. If N is an
$\omega $
-premouse. If N is an
![]() $\omega $
-mouse, we write
$\omega $
-mouse, we write
![]() $\Sigma _N$
for the unique
$\Sigma _N$
for the unique
![]() $(\omega ,\omega _1+1)$
-strategy for N.
$(\omega ,\omega _1+1)$
-strategy for N.
For
![]() $\alpha <\mathrm {Ord}^N$
, recall that
$\alpha <\mathrm {Ord}^N$
, recall that
![]() $\alpha $
is a cutpoint of N iff for all
$\alpha $
is a cutpoint of N iff for all
![]() $E\in \mathbb {E}_+^N$
, if
$E\in \mathbb {E}_+^N$
, if
![]() $\mathrm {cr}(E)<\alpha $
then
$\mathrm {cr}(E)<\alpha $
then
![]() $\mathrm {lh}(E)\leq \alpha $
.
$\mathrm {lh}(E)\leq \alpha $
.
For an extender E,
![]() $t_E$
and
$t_E$
and
![]() $\tau _E$
denote the Dodd parameter and Dodd projectum of E respectively, if they are defined.
$\tau _E$
denote the Dodd parameter and Dodd projectum of E respectively, if they are defined.
2 Extender maximality
In this section we prove Theorems 1.2 and 1.4. The proofs are refinements of less general results proved in [Reference Schlutzenberg6]. Toward these proofs, we begin with a lemma which helps us to find sound hulls of premice; the proof is basically as in [Reference Schlutzenberg11, Lemma 3.1], but here we use the fact that condensation follows from normal iterability in order to reduce our assumptions.
Definition 2.1. Let
![]() $k<\omega $
, let H be k-sound,
$k<\omega $
, let H be k-sound,
![]() $q\in [\rho _0^H]^{<\omega }$
and
$q\in [\rho _0^H]^{<\omega }$
and
![]() $\alpha \in \mathrm {Ord}^H$
. The
$\alpha \in \mathrm {Ord}^H$
. The
![]() $(k+1)$
-solidity witness for
$(k+1)$
-solidity witness for
![]() $(H,q,\alpha )$
, (or just for
$(H,q,\alpha )$
, (or just for
![]() $(q,\alpha )$
), is
$(q,\alpha )$
), is
Letting
![]() $q=\{q_0,\ldots ,q_{\mathrm {lh}(q)-1}\}$
with
$q=\{q_0,\ldots ,q_{\mathrm {lh}(q)-1}\}$
with
![]() $q_i>q_{i+1}$
, the (set of all)
$q_i>q_{i+1}$
, the (set of all)
![]() $(k+1)$
-solidity witnesses for
$(k+1)$
-solidity witnesses for
![]() $(H,q)$
(or just for q) is
$(H,q)$
(or just for q) is
where
![]() $q\!\upharpoonright \! i=\{q_0,\ldots ,q_{i-1}\}$
. The (set of all)
$q\!\upharpoonright \! i=\{q_0,\ldots ,q_{i-1}\}$
. The (set of all)
![]() $(k+1)$
-solidity witnesses for H is
$(k+1)$
-solidity witnesses for H is
Note that in the preceding definition, we are not assuming that the solidity witnesses in consideration are in H.
Definition 2.2. Let
![]() $k<\omega $
, let H be
$k<\omega $
, let H be
![]() $(k+1)$
-sound,
$(k+1)$
-sound,
![]() $q\in \mathfrak {C}_0(H)$
,
$q\in \mathfrak {C}_0(H)$
,
![]() $\theta <\rho _0^H$
,
$\theta <\rho _0^H$
,
![]() $\pi :{\bar {H}}\to H$
be the uncollapse and
$\pi :{\bar {H}}\to H$
be the uncollapse and
![]() $\pi ({\bar {q}})=q$
. We say that
$\pi ({\bar {q}})=q$
. We say that
![]() $(\theta ,q)$
is
$(\theta ,q)$
is
![]() $(k+1)$
-self-solid (for H) iff
$(k+1)$
-self-solid (for H) iff
![]() ${\bar {H}}$
is
${\bar {H}}$
is
![]() $k+1$
-sound and
$k+1$
-sound and
![]() $\rho _{k+1}^{\bar {H}}=\theta $
and
$\rho _{k+1}^{\bar {H}}=\theta $
and
![]() $p_{k+1}^{\bar {H}}=\bar {q}$
.
$p_{k+1}^{\bar {H}}=\bar {q}$
.
Let
![]() $x\in \mathfrak {C}_0(H)$
and
$x\in \mathfrak {C}_0(H)$
and
![]() $r\in [\rho _0^H]^{<\omega }$
. We say that r is an
$r\in [\rho _0^H]^{<\omega }$
. We say that r is an
![]() $\mathrm {r}\Sigma _{k+1}^H(\{x\})$
-generator iff for every
$\mathrm {r}\Sigma _{k+1}^H(\{x\})$
-generator iff for every
![]() $\gamma \in r$
, we have
$\gamma \in r$
, we have
Lemma 2.3. Let
![]() $k<\omega $
and let H be
$k<\omega $
and let H be
![]() $(k+1)$
-sound and
$(k+1)$
-sound and
![]() $(k,\omega _1+1)$
-iterable. Let
$(k,\omega _1+1)$
-iterable. Let
![]() $r\in \mathfrak {C}_0(H)$
and
$r\in \mathfrak {C}_0(H)$
and
![]() $\theta \leq \rho _{k+1}^H$
be a cardinal of H. Then there is
$\theta \leq \rho _{k+1}^H$
be a cardinal of H. Then there is
![]() $q\in H$
such that
$q\in H$
such that
![]() $:$
$:$
-
–
 $(\theta ,q)$
is
$(\theta ,q)$
is
 $(k+1)$
-self-solid for H,
$(k+1)$
-self-solid for H, -
–
 $p_{k+1}^H=q\backslash \min (p_{k+1}^H)$
,
$p_{k+1}^H=q\backslash \min (p_{k+1}^H)$
, -
–
 $r\in \mathrm {Hull}_{k+1}^H(\theta \cup \{\vec {p}_k^H,q\})$
, and
$r\in \mathrm {Hull}_{k+1}^H(\theta \cup \{\vec {p}_k^H,q\})$
, and -
–
 ${\bar {H}}=\mathrm {cHull}_{k+1}^H(\theta \cup \{\vec {p}_k^H,q\})\trianglelefteq H$
.
${\bar {H}}=\mathrm {cHull}_{k+1}^H(\theta \cup \{\vec {p}_k^H,q\})\trianglelefteq H$
.
Proof We may assume H is countable and
![]() $\theta <\rho _{k+1}^H$
. We will define
$\theta <\rho _{k+1}^H$
. We will define
![]() $m<\omega $
and
$m<\omega $
and
with
![]() $q_i>q_{i+1}$
for
$q_i>q_{i+1}$
for
![]() $i+1<m$
. Let
$i+1<m$
. Let
![]() $p=p_{k+1}^H$
. We start with
$p=p_{k+1}^H$
. We start with
![]() $q\!\upharpoonright \!\mathrm {lh}(p)=p$
. We define
$q\!\upharpoonright \!\mathrm {lh}(p)=p$
. We define
![]() $q_i$
for
$q_i$
for
![]() $i\geq \mathrm {lh}(p)$
by induction on i, with
$i\geq \mathrm {lh}(p)$
by induction on i, with
![]() $q_i<\rho _{k+1}^H$
. We simultaneously define an H-cardinal
$q_i<\rho _{k+1}^H$
. We simultaneously define an H-cardinal
![]() $\gamma _i$
, with
$\gamma _i$
, with
![]() $\gamma _{\mathrm {lh}(p)}=\rho _{k+1}^H$
and
$\gamma _{\mathrm {lh}(p)}=\rho _{k+1}^H$
and
![]() $\theta \leq \gamma _{i}\leq q_{i-1}$
for
$\theta \leq \gamma _{i}\leq q_{i-1}$
for
![]() $i>\mathrm {lh}(p)$
, and
$i>\mathrm {lh}(p)$
, and
where
![]() $u_i$
is the set of
$u_i$
is the set of
![]() $(k+1)$
-solidity witnesses for
$(k+1)$
-solidity witnesses for
![]() $(H,q\!\upharpoonright \! i)$
. Now let
$(H,q\!\upharpoonright \! i)$
. Now let
![]() $i\geq \mathrm {lh}(p)$
, and let
$i\geq \mathrm {lh}(p)$
, and let
![]() $q\!\upharpoonright \! i$
,
$q\!\upharpoonright \! i$
,
![]() $\gamma _i$
be given. If
$\gamma _i$
be given. If
![]() $\gamma _i=\theta $
then we set
$\gamma _i=\theta $
then we set
![]() $m=i$
, so
$m=i$
, so
![]() $q=q\!\upharpoonright \! i$
and we are done. So suppose
$q=q\!\upharpoonright \! i$
and we are done. So suppose
![]() $\gamma _i>\theta $
. Let
$\gamma _i>\theta $
. Let
![]() $\eta <\gamma _i$
be least such that
$\eta <\gamma _i$
be least such that
![]() $\eta>\theta $
and
$\eta>\theta $
and
![]() $\eta $
is not a cardinal of H and
$\eta $
is not a cardinal of H and
and
Let
![]() $q_i=\min (\mathrm {Ord}\backslash H_i)=\gamma _i^{+H}\cap H_i$
and let
$q_i=\min (\mathrm {Ord}\backslash H_i)=\gamma _i^{+H}\cap H_i$
and let
![]() $\gamma _i=\mathrm {card}^H(q_i)=\mathrm {card}^H(\eta )$
.
$\gamma _i=\mathrm {card}^H(q_i)=\mathrm {card}^H(\eta )$
.
Clearly
so it suffices to see that
![]() $u_{i+1}\in H_i'$
. Note that the transitive collapse
$u_{i+1}\in H_i'$
. Note that the transitive collapse
![]() $W_i$
of
$W_i$
of
![]() $H_i$
is (equivalent to) the
$H_i$
is (equivalent to) the
![]() $(k+1)$
-solidity witness for
$(k+1)$
-solidity witness for
![]() $(q\!\upharpoonright \! i,q_i)$
, so it suffices to see that
$(q\!\upharpoonright \! i,q_i)$
, so it suffices to see that
![]() $W_i\in H_i'$
. For this, noting that
$W_i\in H_i'$
. For this, noting that
![]() $q_i=\gamma _i^{+W_i}$
, it suffices to see that
$q_i=\gamma _i^{+W_i}$
, it suffices to see that
![]() $W_i\triangleleft H$
, since then
$W_i\triangleleft H$
, since then
![]() $W_i$
is the least segment W of H such that
$W_i$
is the least segment W of H such that
![]() $\mathrm {Ord}^W\geq q_i$
and
$\mathrm {Ord}^W\geq q_i$
and
![]() $\rho _\omega ^W=\gamma _i=\mathrm {lgcd}(H|q_i)$
.
$\rho _\omega ^W=\gamma _i=\mathrm {lgcd}(H|q_i)$
.
Let
![]() $\rho =q_i$
and
$\rho =q_i$
and
![]() $\gamma =\gamma _i$
and
$\gamma =\gamma _i$
and
![]() $W=W_i$
. Let
$W=W_i$
. Let
![]() $\pi :W\to H$
be the uncollapse. Then
$\pi :W\to H$
be the uncollapse. Then
![]() $\pi (p_{k+1}^W\backslash \rho )=q\!\upharpoonright \! i$
and W is
$\pi (p_{k+1}^W\backslash \rho )=q\!\upharpoonright \! i$
and W is
![]() $\rho $
-sound and
$\rho $
-sound and
![]() $\mathrm {cr}(\pi )=\rho $
and
$\mathrm {cr}(\pi )=\rho $
and
(
![]() $\rho _{k+1}^{W}\geq \gamma $
because
$\rho _{k+1}^{W}\geq \gamma $
because
![]() $W\in H$
, and
$W\in H$
, and
![]() $\rho _{k+1}^W<\rho $
because
$\rho _{k+1}^W<\rho $
because
![]() $\eta <\rho $
and by line (1)). So by condensation as stated in [Reference Schlutzenberg9, Theorem 5.2], either (a)
$\eta <\rho $
and by line (1)). So by condensation as stated in [Reference Schlutzenberg9, Theorem 5.2], either (a)
![]() $W\triangleleft H$
or (b) letting
$W\triangleleft H$
or (b) letting
![]() $J\triangleleft H$
be least such that
$J\triangleleft H$
be least such that
![]() $q_i\leq \mathrm {Ord}^J$
and
$q_i\leq \mathrm {Ord}^J$
and
![]() $\rho _\omega ^J=\gamma $
, then
$\rho _\omega ^J=\gamma $
, then
![]() $\rho _{k+1}^J=\gamma <\rho _k^J$
and there is a type 1 extender F over J with
$\rho _{k+1}^J=\gamma <\rho _k^J$
and there is a type 1 extender F over J with
![]() $\mathrm {cr}(F)=\gamma $
and
$\mathrm {cr}(F)=\gamma $
and
![]() $W=\mathrm {Ult}_k(J,F)$
. But since
$W=\mathrm {Ult}_k(J,F)$
. But since
![]() $\eta>\gamma $
and because of line (2), we have
$\eta>\gamma $
and because of line (2), we have
and therefore (b) is false. So
![]() $W\triangleleft H$
, as required.
$W\triangleleft H$
, as required.
Since
![]() $\gamma _{i+1}<\gamma _i$
, the construction terminates successfully.
$\gamma _{i+1}<\gamma _i$
, the construction terminates successfully.
Finally, the fact that
![]() ${\bar {H}}\trianglelefteq H$
(where
${\bar {H}}\trianglelefteq H$
(where
![]() ${\bar {H}}$
is defined in the statement of the theorem) follows from condensation.
${\bar {H}}$
is defined in the statement of the theorem) follows from condensation.
Related calculations also give the following:
Lemma 2.4. Let
![]() $k<\omega $
and let H be
$k<\omega $
and let H be
![]() $(k+1)$
-sound and
$(k+1)$
-sound and
![]() $(k,\omega _1+1)$
-iterable. Suppose
$(k,\omega _1+1)$
-iterable. Suppose
![]() $\rho =\rho _{k+1}^H=\kappa ^{+H}>\omega $
and
$\rho =\rho _{k+1}^H=\kappa ^{+H}>\omega $
and
![]() $\kappa $
is an H-cardinal. For
$\kappa $
is an H-cardinal. For
![]() $\gamma <\rho $
let
$\gamma <\rho $
let
and
![]() $W_\gamma $
be the transitive collapse of
$W_\gamma $
be the transitive collapse of
![]() $H_\gamma $
. Then
$H_\gamma $
. Then
![]() $:$
$:$
-
(i) For all sufficiently large
 $\gamma \in (\kappa ,\rho )$
, either
$\gamma \in (\kappa ,\rho )$
, either
 $:$
$:$
-
–
 $W_\gamma \triangleleft H$
, or
$W_\gamma \triangleleft H$
, or -
–
 $\kappa ^{+W_\gamma }=\rho _\omega ^{W_\gamma }=\gamma $
,
$\kappa ^{+W_\gamma }=\rho _\omega ^{W_\gamma }=\gamma $
,
 $H|\gamma $
is active with E
Footnote
7
and
$H|\gamma $
is active with E
Footnote
7
and
 $W_\gamma \triangleleft \mathrm {Ult}(H,E)$
.
$W_\gamma \triangleleft \mathrm {Ult}(H,E)$
.
-
-
(ii) For cofinally many
 $\gamma <\rho $
, we have
$\gamma <\rho $
, we have
 $W_\gamma \triangleleft H$
and
$W_\gamma \triangleleft H$
and
 $\rho _{k+1}^{W_\gamma }=\kappa $
.
$\rho _{k+1}^{W_\gamma }=\kappa $
.
Proof For
![]() $\gamma \in (\kappa ,\rho )$
, say that
$\gamma \in (\kappa ,\rho )$
, say that
![]() $\gamma $
is a generator iff
$\gamma $
is a generator iff
![]() $\gamma \notin H_\gamma $
. We say that a generator is a limit generator iff it is a limit of generators, and is otherwise a successor generator. Note that the set of generators above
$\gamma \notin H_\gamma $
. We say that a generator is a limit generator iff it is a limit of generators, and is otherwise a successor generator. Note that the set of generators above
![]() $\kappa $
is club in
$\kappa $
is club in
![]() $\rho $
. Let
$\rho $
. Let
![]() $\gamma>\kappa $
be a generator. Then note that
$\gamma>\kappa $
be a generator. Then note that
![]() $W_\gamma \in H$
and
$W_\gamma \in H$
and
![]() $\gamma =\kappa ^{+W_\gamma }$
so
$\gamma =\kappa ^{+W_\gamma }$
so
![]() $\rho _{k+1}^{W_\gamma }\in \{\kappa ,\gamma \}$
; moreover, if
$\rho _{k+1}^{W_\gamma }\in \{\kappa ,\gamma \}$
; moreover, if
![]() $\gamma $
is a successor generator then
$\gamma $
is a successor generator then
![]() $\rho _{k+1}^{W_\gamma }=\kappa $
.
$\rho _{k+1}^{W_\gamma }=\kappa $
.
Now let
![]() $\eta _0$
be the least generator
$\eta _0$
be the least generator
![]() $\gamma>\kappa $
such that
$\gamma>\kappa $
such that
![]() $w_{k+1}^H\in H_\gamma $
. We claim that the conclusion of (i) holds for all generators
$w_{k+1}^H\in H_\gamma $
. We claim that the conclusion of (i) holds for all generators
![]() $\gamma>\eta _0$
. We proceed by induction on
$\gamma>\eta _0$
. We proceed by induction on
![]() $\gamma $
.
$\gamma $
.
First suppose that
![]() $\gamma $
is a limit generator. Then by induction, for eventually all successor generators
$\gamma $
is a limit generator. Then by induction, for eventually all successor generators
![]() $\gamma '<\gamma $
, we have
$\gamma '<\gamma $
, we have
![]() $W_{\gamma '}\triangleleft H$
and
$W_{\gamma '}\triangleleft H$
and
![]() $\gamma '=\kappa ^{+W_{\gamma '}}$
and
$\gamma '=\kappa ^{+W_{\gamma '}}$
and
![]() $W_{\gamma '}$
projects to
$W_{\gamma '}$
projects to
![]() $\kappa $
. It follows that
$\kappa $
. It follows that
![]() $W_{\gamma '}\in H_\gamma $
, so
$W_{\gamma '}\in H_\gamma $
, so
![]() $W_{\gamma '}\in W_\gamma $
, which implies that
$W_{\gamma '}\in W_\gamma $
, which implies that
![]() $\rho _{k+1}^{W_{\gamma }}=\gamma $
, and therefore
$\rho _{k+1}^{W_{\gamma }}=\gamma $
, and therefore
![]() $W_\gamma $
is
$W_\gamma $
is
![]() $(k+1)$
-sound. So the conclusion for
$(k+1)$
-sound. So the conclusion for
![]() $W_\gamma $
follows from
$W_\gamma $
follows from
![]() $(k+1)$
-condensation.
$(k+1)$
-condensation.
Now suppose that
![]() $\gamma $
is a successor generator. Then there is a largest generator
$\gamma $
is a successor generator. Then there is a largest generator
![]() $\eta <\gamma $
, and we have
$\eta <\gamma $
, and we have
![]() $\kappa <\eta _0\leq \eta <\gamma $
, and
$\kappa <\eta _0\leq \eta <\gamma $
, and
![]() $W_\gamma $
projects to
$W_\gamma $
projects to
![]() $\kappa $
. So using condensation (as stated in [Reference Schlutzenberg9, Theorem 5.2]) as in the proof of 2.3, we get
$\kappa $
. So using condensation (as stated in [Reference Schlutzenberg9, Theorem 5.2]) as in the proof of 2.3, we get
![]() $W_\gamma \triangleleft H$
.
$W_\gamma \triangleleft H$
.
Part (ii) now easily follows; in fact its conclusion holds for every sufficiently large successor generator.
Remark 2.5. Let M be an m-sound premouse. Recall that a (putative) iteration tree on M is m-maximal given that (i)
![]() $\mathcal {T}$
satisfies the monotone length condition
$\mathcal {T}$
satisfies the monotone length condition
and for each
![]() $\alpha +1<\mathrm {lh}(\mathcal {T})$
, (ii)
$\alpha +1<\mathrm {lh}(\mathcal {T})$
, (ii)
![]() $\gamma =\mathrm {pred}^{\mathcal {T}}(\alpha +1)$
is least such that
$\gamma =\mathrm {pred}^{\mathcal {T}}(\alpha +1)$
is least such that
![]() $\mathrm {cr}(E^{\mathcal {T}}_\alpha )<\nu (E^{\mathcal {T}}_\gamma )$
, (iii)
$\mathrm {cr}(E^{\mathcal {T}}_\alpha )<\nu (E^{\mathcal {T}}_\gamma )$
, (iii)
![]() $M^{*\mathcal {T}}_{\alpha +1}\trianglelefteq M^{\mathcal {T}}_\gamma $
is as large as possible, and (iv)
$M^{*\mathcal {T}}_{\alpha +1}\trianglelefteq M^{\mathcal {T}}_\gamma $
is as large as possible, and (iv)
![]() $k=\deg ^{\mathcal {T}}_{\alpha +1}$
is as large as possible subject to the choice of
$k=\deg ^{\mathcal {T}}_{\alpha +1}$
is as large as possible subject to the choice of
![]() $M^{*\mathcal {T}}_{\alpha +1}$
(with
$M^{*\mathcal {T}}_{\alpha +1}$
(with
![]() $k\leq \deg ^{\mathcal {T}}_\gamma $
if
$k\leq \deg ^{\mathcal {T}}_\gamma $
if
![]() $M^{*\mathcal {T}}_{\alpha +1}=M^{\mathcal {T}}_\gamma $
).
$M^{*\mathcal {T}}_{\alpha +1}=M^{\mathcal {T}}_\gamma $
).
Definition 2.6. Let M be an m-sound premouse. An essentially m-maximal tree on M satisfies the requirements of m-maximality, except that we drop the monotone length condition, replacing it with the monotone
![]() $\nu $
condition, that is, that
$\nu $
condition, that is, that
Remark 2.7. It is easy to see that, for example,
![]() $(m,\omega _1+1)$
-iterability is equivalent to essential-
$(m,\omega _1+1)$
-iterability is equivalent to essential-
![]() $(m,\omega _1+1)$
-iterability.
$(m,\omega _1+1)$
-iterability.
Definition 2.8. Let
![]() $\pi :\mathfrak {C}_0(M)\to \mathfrak {C}_0(N)$
be
$\pi :\mathfrak {C}_0(M)\to \mathfrak {C}_0(N)$
be
![]() $\Sigma _0$
-elementary between premice
$\Sigma _0$
-elementary between premice
![]() $M,N$
of the same type.
$M,N$
of the same type.
If
![]() $M,N$
are passive then
$M,N$
are passive then
![]() $\psi _\pi $
denotes
$\psi _\pi $
denotes
![]() $\pi $
. If
$\pi $
. If
![]() $M,N$
are active,
$M,N$
are active,
![]() $\mu =\mathrm {cr}(F^M)$
and
$\mu =\mathrm {cr}(F^M)$
and
![]() $\kappa =\mathrm {cr}(F^N)$
, then
$\kappa =\mathrm {cr}(F^N)$
, then
denotes the embedding induced by the Shift Lemma from
![]() $\pi $
. So in both cases,
$\pi $
. So in both cases,
![]() $\pi \subseteq \psi _\pi $
and
$\pi \subseteq \psi _\pi $
and
![]() $\psi _\pi $
is fully elementary.
$\psi _\pi $
is fully elementary.
Now we say that
![]() $\pi $
is:
$\pi $
is:
-
–
 $\nu $
-low iff
$\nu $
-low iff
 $M,N$
are type 3 and
$M,N$
are type 3 and
 $\psi _\pi (\nu ^M)<\nu ^N$
,
$\psi _\pi (\nu ^M)<\nu ^N$
, -
–
 $\nu $
-preserving iff [if
$\nu $
-preserving iff [if
 $M,N$
are type 3 then
$M,N$
are type 3 then
 $\psi _\pi (\nu ^M)=\nu ^N$
], and
$\psi _\pi (\nu ^M)=\nu ^N$
], and -
–
 $\nu $
-high iff
$\nu $
-high iff
 $M,N$
are type 3 and
$M,N$
are type 3 and
 $\psi _\pi (\nu ^M)>\nu ^N$
.
$\psi _\pi (\nu ^M)>\nu ^N$
.
Remark 2.9. Suppose
![]() $\pi ,M,N$
are as above and
$\pi ,M,N$
are as above and
![]() $M,N$
are type 3. It is easy to see that if
$M,N$
are type 3. It is easy to see that if
![]() $\pi $
is
$\pi $
is
![]() $\mathrm {r}\Sigma _2$
-elementary then
$\mathrm {r}\Sigma _2$
-elementary then
![]() $\pi $
is
$\pi $
is
![]() $\nu $
-preserving, and if
$\nu $
-preserving, and if
![]() $\pi $
is
$\pi $
is
![]() $\mathrm {r}\Sigma _1$
-elementary then
$\mathrm {r}\Sigma _1$
-elementary then
![]() $\pi $
is non-
$\pi $
is non-
![]() $\nu $
-low. Moreover, one can show that if
$\nu $
-low. Moreover, one can show that if
![]() $\pi =\pi _0$
is a
$\pi =\pi _0$
is a
![]() $\nu $
-preserving near k-embedding, then the copying construction for k-maximal (or essentially k-maximal) trees with
$\nu $
-preserving near k-embedding, then the copying construction for k-maximal (or essentially k-maximal) trees with
![]() $\pi $
preserves tree order, and for each
$\pi $
preserves tree order, and for each
![]() $\alpha $
,
$\alpha $
,
![]() $\pi _\alpha $
is a
$\pi _\alpha $
is a
![]() $\nu $
-preserving near
$\nu $
-preserving near
![]() $\deg ^{\mathcal {T}}_\alpha $
-embedding. (Here if
$\deg ^{\mathcal {T}}_\alpha $
-embedding. (Here if
![]() $M^{\mathcal {T}}_\alpha $
is type 3 and
$M^{\mathcal {T}}_\alpha $
is type 3 and
![]() $\rho _0(M^{\mathcal {T}}_\alpha )<\mathrm {lh}(E^{\mathcal {T}}_\alpha )<\mathrm {Ord}(M^{\mathcal {T}}_\alpha )$
then we copy
$\rho _0(M^{\mathcal {T}}_\alpha )<\mathrm {lh}(E^{\mathcal {T}}_\alpha )<\mathrm {Ord}(M^{\mathcal {T}}_\alpha )$
then we copy
![]() $E^{\mathcal {T}}_\alpha $
to
$E^{\mathcal {T}}_\alpha $
to
![]() $E^{\mathcal {U}}_\alpha =\psi _{\pi _\alpha }(E^{\mathcal {T}}_\alpha )$
.)
$E^{\mathcal {U}}_\alpha =\psi _{\pi _\alpha }(E^{\mathcal {T}}_\alpha )$
.)
Definition 2.10. Let M be an active premouse,
![]() $F=F^M$
and
$F=F^M$
and
![]() $\kappa =\mathrm {cr}(F)$
. We say F is of superstrong type iff
$\kappa =\mathrm {cr}(F)$
. We say F is of superstrong type iff
![]() $i^M_F(\kappa )$
is the largest cardinal of M. We say a premouse N is below superstrong iff no
$i^M_F(\kappa )$
is the largest cardinal of M. We say a premouse N is below superstrong iff no
![]() $E\in \mathbb {E}_+^N$
is of superstrong type.
$E\in \mathbb {E}_+^N$
is of superstrong type.
We will primarily be interested in extenders whose support is of form
![]() $\sigma \cup t$
where
$\sigma \cup t$
where
![]() $\sigma \in \mathrm {Ord}$
and t is a finite set of ordinals. However, we do not want to assume explicitly that the “ordinals” in t are in fact wellfounded, and we want to allow that there are other “ordinals” of the ultrapower below “
$\sigma \in \mathrm {Ord}$
and t is a finite set of ordinals. However, we do not want to assume explicitly that the “ordinals” in t are in fact wellfounded, and we want to allow that there are other “ordinals” of the ultrapower below “
![]() $\max (t)$
” which are not themselves in the support. (This can be the case, for example, for an extender of form
$\max (t)$
” which are not themselves in the support. (This can be the case, for example, for an extender of form
![]() $E\!\upharpoonright \!(\tau _E\cup t_E)$
.) Toward this we adopt the following terminology:
$E\!\upharpoonright \!(\tau _E\cup t_E)$
.) Toward this we adopt the following terminology:
Definition 2.11. Say a short extender E over
![]() $\kappa =\mathrm {cr}(E)$
is standard if it has support
$\kappa =\mathrm {cr}(E)$
is standard if it has support
![]() $\sigma +n$
for some limit ordinal
$\sigma +n$
for some limit ordinal
![]() $\sigma $
and
$\sigma $
and
![]() $n<\omega $
, (so
$n<\omega $
, (so
![]() $E=\left <E_a\right>_{a\in [\sigma +n]^{<\omega }}$
),
$E=\left <E_a\right>_{a\in [\sigma +n]^{<\omega }}$
),
![]() $[\kappa ]^{|a|}\in E_a$
for each
$[\kappa ]^{|a|}\in E_a$
for each
![]() $a\in [\sigma +n]^{<\omega }$
, and letting
$a\in [\sigma +n]^{<\omega }$
, and letting
![]() $\mathrm {id}':[\kappa ]^1\to \kappa $
be the function
$\mathrm {id}':[\kappa ]^1\to \kappa $
be the function
![]() $\mathrm {id}'(\{\alpha \})=\alpha $
, for each
$\mathrm {id}'(\{\alpha \})=\alpha $
, for each
![]() $\alpha <\sigma $
, we have
$\alpha <\sigma $
, we have
![]() $[\{\alpha \},\mathrm {id}']_E=\alpha $
. (We follow the usual conventions regarding how
$[\{\alpha \},\mathrm {id}']_E=\alpha $
. (We follow the usual conventions regarding how
![]() $E_{a\cup b}$
projects to
$E_{a\cup b}$
projects to
![]() $E_a$
when
$E_a$
when
![]() $a,b\in [\sigma +n]^{<\omega }$
. So for each
$a,b\in [\sigma +n]^{<\omega }$
. So for each
![]() $\alpha <\sigma $
and
$\alpha <\sigma $
and
![]() $m_0\leq m_1<n$
,
$m_0\leq m_1<n$
,
![]() $[\{\sigma +m_i\},\mathrm {id}']_E$
represents an “ordinal”
$[\{\sigma +m_i\},\mathrm {id}']_E$
represents an “ordinal”
![]() $\beta _i$
of the ultrapower and the ultrapower satisfies “
$\beta _i$
of the ultrapower and the ultrapower satisfies “
![]() $\alpha <\beta _0<\beta _1$
”, though we do not assume that
$\alpha <\beta _0<\beta _1$
”, though we do not assume that
![]() $\beta _0,\beta _1$
are in the wellfounded part of the ultrapower.)
$\beta _0,\beta _1$
are in the wellfounded part of the ultrapower.)
In what follows, in the above context, when
![]() $n>0$
, we typically write t for
$n>0$
, we typically write t for
![]() $\{\sigma ,\ldots ,\sigma {\kern-1pt}+{\kern-1pt}n{\kern-1pt}-{\kern-1pt}1\}$
, but may also identify t with the finite set
$\{\sigma ,\ldots ,\sigma {\kern-1pt}+{\kern-1pt}n{\kern-1pt}-{\kern-1pt}1\}$
, but may also identify t with the finite set
![]() $\{[\{\sigma {\kern-1pt}+{\kern-1pt}m\},\mathrm {id}']_E\bigm |m{\kern-1pt}<{\kern-1pt}n\}$
of ordinals of the ultrapower.
$\{[\{\sigma {\kern-1pt}+{\kern-1pt}m\},\mathrm {id}']_E\bigm |m{\kern-1pt}<{\kern-1pt}n\}$
of ordinals of the ultrapower.
We will deduce Theorems 1.2 and 1.4 from the following:
Theorem 2.12. Let N be a
![]() $(0,\omega _1+1)$
-iterable premouse,
$(0,\omega _1+1)$
-iterable premouse,
![]() $F\in N$
and
$F\in N$
and
![]() $\mu ,\sigma \in \mathrm {Ord}^N$
,
$\mu ,\sigma \in \mathrm {Ord}^N$
,
![]() $\ell <\omega $
and W be such that
$\ell <\omega $
and W be such that
![]() $:$
$:$
-
–
 $\sigma $
is an N-cardinal,
$\sigma $
is an N-cardinal, -
– F is a standard short N-extender with support
 $\sigma +\ell $
, weakly amenable to N, coded as a subset of
$\sigma +\ell $
, weakly amenable to N, coded as a subset of
 $N|\sigma $
, such that
$N|\sigma $
, such that
 $N\models $
“F is countably complete”,
$N\models $
“F is countably complete”, -
–
 $W=\mathrm {Ult}_0(N,F)$
,
$W=\mathrm {Ult}_0(N,F)$
,
 $\mu =\mathrm {cr}(F)<\sigma $
and
$\mu =\mathrm {cr}(F)<\sigma $
and
 $\mathcal {H}_\sigma ^N\subseteq W$
.
$\mathcal {H}_\sigma ^N\subseteq W$
.
Then (i)
![]() $W|\sigma ^{+W}=N||\sigma ^{+W}$
and if
$W|\sigma ^{+W}=N||\sigma ^{+W}$
and if
![]() $\ell =0$
then (ii)
$\ell =0$
then (ii)
![]() $F\in \mathbb {E}_+^{N}$
.
$F\in \mathbb {E}_+^{N}$
.
Proof We may assume that
![]() $N=\mathcal {J}(R)$
where F is definable from parameters over R and
$N=\mathcal {J}(R)$
where F is definable from parameters over R and
![]() $\rho _\omega ^R=\sigma $
. Say that F is
$\rho _\omega ^R=\sigma $
. Say that F is
![]() $\mathrm {r}\Sigma _{n+1}^R(\{r\})$
. We may also assume inductively that all segments of R satisfy the theorem.
$\mathrm {r}\Sigma _{n+1}^R(\{r\})$
. We may also assume inductively that all segments of R satisfy the theorem.
Let
![]() $n\ll m<\omega $
and
$n\ll m<\omega $
and
![]() $M=\mathrm {cHull}_{m+1}^R(\{s\})$
where
$M=\mathrm {cHull}_{m+1}^R(\{s\})$
where
![]() $(\omega ,s)$
is
$(\omega ,s)$
is
![]() $(m+1)$
-self-solid for R and
$(m+1)$
-self-solid for R and
![]() $r\in \mathrm {rg}(\pi _{MR})$
where
$r\in \mathrm {rg}(\pi _{MR})$
where
![]() $\pi _{MR}:M\to R$
is the uncollapse.
$\pi _{MR}:M\to R$
is the uncollapse.
Let
![]() $E=(\pi _{MR}^{-1})"F$
. So E is a standard M-extender with support
$E=(\pi _{MR}^{-1})"F$
. So E is a standard M-extender with support
![]() $\tau +\ell $
, where either
$\tau +\ell $
, where either
![]() $\tau <\rho _0^M$
and
$\tau <\rho _0^M$
and
![]() $\pi _{MR}(\tau )=\sigma $
, or
$\pi _{MR}(\tau )=\sigma $
, or
![]() $\tau =\rho _0^M$
and
$\tau =\rho _0^M$
and
![]() $\rho _0^R=\sigma $
. And E is
$\rho _0^R=\sigma $
. And E is ![]() -definable, M is
-definable, M is
![]() $(m+1)$
-sound,
$(m+1)$
-sound,
![]() $n+10< m$
and
$n+10< m$
and
Other relevant properties of
![]() $(R,F)$
also reflect to
$(R,F)$
also reflect to
![]() $(M,E)$
. Moreover,
$(M,E)$
. Moreover,
by the countable completeness of F in N and the
![]() $(\omega ,\omega _1+1)$
-iterability of R.
$(\omega ,\omega _1+1)$
-iterability of R.
Now
![]() $\tau <\mathrm {Ord}^M$
. For suppose
$\tau <\mathrm {Ord}^M$
. For suppose
![]() $\tau =\mathrm {Ord}^M$
. Since
$\tau =\mathrm {Ord}^M$
. Since
![]() $\rho _{n+10}^M=\tau $
, therefore M is passive. If
$\rho _{n+10}^M=\tau $
, therefore M is passive. If
![]() $\tau =\kappa ^{+M}$
(that is,
$\tau =\kappa ^{+M}$
(that is,
![]() $\kappa $
is the largest cardinal of M), then we have
$\kappa $
is the largest cardinal of M), then we have
![]() ${U|\kappa ^{+M}=M|\kappa ^{+M}=M}$
(by condensation for M), but then
${U|\kappa ^{+M}=M|\kappa ^{+M}=M}$
(by condensation for M), but then
![]() $E\in U$
, which is impossible. So
$E\in U$
, which is impossible. So
![]() $\tau>\kappa ^{+M}$
. Then
$\tau>\kappa ^{+M}$
. Then
![]() $E\!\upharpoonright \!\eta \in M$
for all
$E\!\upharpoonright \!\eta \in M$
for all
![]() $\eta <\tau $
(since
$\eta <\tau $
(since
![]() $\rho _{n+10}^M=\tau $
), so by induction (with conclusion (i) of the theorem),
$\rho _{n+10}^M=\tau $
), so by induction (with conclusion (i) of the theorem),
![]() $U|\tau =M|\tau =M$
, so again,
$U|\tau =M|\tau =M$
, so again,
![]() $E\in U$
, a contradiction.
$E\in U$
, a contradiction.
Let
![]() $\theta $
be the largest M-cardinal
$\theta $
be the largest M-cardinal
![]() $\leq \tau $
such that
$\leq \tau $
such that
![]() $M|\theta =U|\theta $
.Footnote
8
Let t be
$M|\theta =U|\theta $
.Footnote
8
Let t be
![]() $(m,\omega )$
-self-solid for M, and such that letting
$(m,\omega )$
-self-solid for M, and such that letting
and
![]() $\pi :\bar {M}\to M$
be the uncollapse, then
$\pi :\bar {M}\to M$
be the uncollapse, then
![]() $r,s\in \mathrm {rg}(\pi _{MR}\circ \pi )$
, and
$r,s\in \mathrm {rg}(\pi _{MR}\circ \pi )$
, and
![]() $\tau \in \mathrm {rg}(\pi )$
if
$\tau \in \mathrm {rg}(\pi )$
if
![]() $\tau <\rho _0^M$
, and
$\tau <\rho _0^M$
, and
![]() $\theta \in \mathrm {rg}(\pi )$
if
$\theta \in \mathrm {rg}(\pi )$
if
![]() $\theta <\rho _0^M$
. Let
$\theta <\rho _0^M$
. Let
![]() $\pi (\bar {t})=t$
, etc., and
$\pi (\bar {t})=t$
, etc., and
![]() $\bar {E}=(\pi ^{-1})"E$
, etc. So
$\bar {E}=(\pi ^{-1})"E$
, etc. So
![]() $\bar {E}$
is defined over
$\bar {E}$
is defined over
![]() $\bar {M}$
from
$\bar {M}$
from
![]() $\bar {t}$
just as E is over M from t, and the relevant properties of
$\bar {t}$
just as E is over M from t, and the relevant properties of
![]() $(M,E,U)$
reflect to
$(M,E,U)$
reflect to
![]() $(\bar {M},\bar {E},\bar {U})$
, where
$(\bar {M},\bar {E},\bar {U})$
, where
![]() $\bar {U}=\mathrm {Ult}_{m-1}(\bar {M},\bar {E})$
.
$\bar {U}=\mathrm {Ult}_{m-1}(\bar {M},\bar {E})$
.
Let
![]() $\pi (\bar {\theta })=\theta $
if
$\pi (\bar {\theta })=\theta $
if
![]() $\theta <\rho _0^M$
, and otherwise
$\theta <\rho _0^M$
, and otherwise
![]() $\bar {\theta }=\rho _0^{\bar {M}}$
. Likewise for
$\bar {\theta }=\rho _0^{\bar {M}}$
. Likewise for
![]() $\bar {\tau }$
. So
$\bar {\tau }$
. So
![]() $\bar {\theta },\bar {\tau }$
have the same defining properties with respect to
$\bar {\theta },\bar {\tau }$
have the same defining properties with respect to
![]() $\bar {M},\bar {U}$
. Define the phalanx (see [Reference Schlutzenberg11, Section 1.1] for the notation)
$\bar {M},\bar {U}$
. Define the phalanx (see [Reference Schlutzenberg11, Section 1.1] for the notation)
Claim 1.
![]() $\mathfrak {P}$
is
$\mathfrak {P}$
is
![]() $(\omega _1+1)$
-iterable.
$(\omega _1+1)$
-iterable.
Proof We will lift trees on
![]() $\mathfrak {P}$
to essentially m-maximal trees on U, which by 2.7 and line (3) suffices. Let
$\mathfrak {P}$
to essentially m-maximal trees on U, which by 2.7 and line (3) suffices. Let
![]() $\psi :\bar {U}\to U$
be the Shift Lemma map. Let
$\psi :\bar {U}\to U$
be the Shift Lemma map. Let
![]() $\theta '=\sup \pi "\bar {\theta }$
.
$\theta '=\sup \pi "\bar {\theta }$
.
Case 1.
![]() $\theta '<\theta $
.
$\theta '<\theta $
.
Let
![]() $\gamma =\mathrm {card}^{M}(\theta ')$
, so
$\gamma =\mathrm {card}^{M}(\theta ')$
, so
![]() $\gamma <\theta $
. Let
$\gamma <\theta $
. Let
![]() $t'$
be such that
$t'$
be such that
![]() $(\gamma ,t')$
is m-self-solid for M, with
$(\gamma ,t')$
is m-self-solid for M, with
and
![]() $\widetilde {\pi }:M'\to M$
be the uncollapse, such that
$\widetilde {\pi }:M'\to M$
be the uncollapse, such that
![]() $t\in \mathrm {rg}(\widetilde {\pi })$
. Let
$t\in \mathrm {rg}(\widetilde {\pi })$
. Let
![]() $\pi ':\bar {M}\to M'$
be
$\pi ':\bar {M}\to M'$
be
![]() ${\pi '=\widetilde {\pi }^{-1}\circ \pi }$
. So
${\pi '=\widetilde {\pi }^{-1}\circ \pi }$
. So
Note that
![]() $\mathrm {Ord}^{M'}<\theta $
, so
$\mathrm {Ord}^{M'}<\theta $
, so
![]() $M'\triangleleft U$
.
$M'\triangleleft U$
.
We can use
![]() $(\pi ',\psi )$
to lift trees
$(\pi ',\psi )$
to lift trees
![]() $\mathcal {T}$
on
$\mathcal {T}$
on
![]() $\mathfrak {P}$
to essentially m-maximal trees
$\mathfrak {P}$
to essentially m-maximal trees
![]() $\mathcal {U}$
on U. In case
$\mathcal {U}$
on U. In case
![]() $\theta $
is a limit cardinal of M then everything here is routine (and we actually get m-maximal trees on U). So assume that
$\theta $
is a limit cardinal of M then everything here is routine (and we actually get m-maximal trees on U). So assume that
![]() $\theta =\gamma ^{+M}$
. Most of the details of the copying process are routine, but we explain enough that we can point out how the wrinkles are dealt with. Let
$\theta =\gamma ^{+M}$
. Most of the details of the copying process are routine, but we explain enough that we can point out how the wrinkles are dealt with. Let
![]() $\pi (\bar {\gamma })=\gamma $
. For
$\pi (\bar {\gamma })=\gamma $
. For
![]() $\alpha <\mathrm {lh}(\mathcal {T})$
with
$\alpha <\mathrm {lh}(\mathcal {T})$
with
![]() $\alpha>0$
, let
$\alpha>0$
, let
![]() $\mathrm {root}^{\mathcal {T}}_\alpha =0$
if
$\mathrm {root}^{\mathcal {T}}_\alpha =0$
if
![]() $M^{\mathcal {T}}_\alpha $
is above
$M^{\mathcal {T}}_\alpha $
is above
![]() $\bar {U}$
, and
$\bar {U}$
, and
![]() $\mathrm {root}^{\mathcal {T}}_\alpha =-1$
if above
$\mathrm {root}^{\mathcal {T}}_\alpha =-1$
if above
![]() $\bar {M}$
. Let
$\bar {M}$
. Let
![]() $\alpha <\mathrm {lh}(\mathcal {T})$
. If
$\alpha <\mathrm {lh}(\mathcal {T})$
. If
![]() $\mathrm {root}^{\mathcal {T}}_\alpha =0$
then the copy map
$\mathrm {root}^{\mathcal {T}}_\alpha =0$
then the copy map
is produced routinely. Suppose
![]() $\mathrm {root}^{\mathcal {T}}_\alpha =-1$
. If
$\mathrm {root}^{\mathcal {T}}_\alpha =-1$
. If
![]() $(-1,\alpha ]_{\mathcal {T}}$
does not drop in model and
$(-1,\alpha ]_{\mathcal {T}}$
does not drop in model and
(note this does not include
![]() $\beta =-1$
, so we are allowing
$\beta =-1$
, so we are allowing
![]() $\bar {\gamma }=\mathrm {cr}(i^{\mathcal {T}}_{-1,\alpha })$
), then
$\bar {\gamma }=\mathrm {cr}(i^{\mathcal {T}}_{-1,\alpha })$
), then
![]() $[0,\alpha ]_{\mathcal {U}}$
does not drop in model or degree and
$[0,\alpha ]_{\mathcal {U}}$
does not drop in model or degree and
and
![]() $\pi _\alpha $
is an
$\pi _\alpha $
is an
![]() $(m-1)$
-lifting embedding which is produced in the obvious manner via the Shift Lemma. Otherwise,
$(m-1)$
-lifting embedding which is produced in the obvious manner via the Shift Lemma. Otherwise,
![]() $(0,\alpha ]_{\mathcal {U}}$
drops in model, and
$(0,\alpha ]_{\mathcal {U}}$
drops in model, and
![]() $\pi _\alpha :M^{\mathcal {T}}_\alpha \to M^{\mathcal {U}}_\alpha $
, which is again produced in the obvious manner. We copy extenders using these maps. There is a wrinkle when
$\pi _\alpha :M^{\mathcal {T}}_\alpha \to M^{\mathcal {U}}_\alpha $
, which is again produced in the obvious manner. We copy extenders using these maps. There is a wrinkle when
![]() $\mathrm {pred}^{\mathcal {T}}(\alpha +1)=-1$
and
$\mathrm {pred}^{\mathcal {T}}(\alpha +1)=-1$
and
![]() $\mathrm {cr}(E^{\mathcal {T}}_\alpha )=\bar {\gamma }$
, so consider this case. We have then
$\mathrm {cr}(E^{\mathcal {T}}_\alpha )=\bar {\gamma }$
, so consider this case. We have then
![]() $\mathrm {cr}(E^{\mathcal {U}}_\alpha )=\gamma $
. Because
$\mathrm {cr}(E^{\mathcal {U}}_\alpha )=\gamma $
. Because
and
we get
![]() $M^{*\mathcal {T}}_{\alpha +1}=\bar {M}$
, and
$M^{*\mathcal {T}}_{\alpha +1}=\bar {M}$
, and
![]() $M^{*\mathcal {U}}_{\alpha +1}=U$
(not
$M^{*\mathcal {U}}_{\alpha +1}=U$
(not
![]() $M'$
), and
$M'$
), and
![]() $M'\triangleleft U|\theta $
. Now if
$M'\triangleleft U|\theta $
. Now if
![]() $E^{\mathcal {U}}_\alpha $
is not of superstrong type then
$E^{\mathcal {U}}_\alpha $
is not of superstrong type then
and
and things are standard. However, if
![]() $E^{\mathcal {U}}_\alpha $
is of superstrong type, then
$E^{\mathcal {U}}_\alpha $
is of superstrong type, then
so when we lift
![]() $E^{\mathcal {T}}_{\alpha +1}$
, we get
$E^{\mathcal {T}}_{\alpha +1}$
, we get
![]() $\mathrm {lh}(E^{\mathcal {U}}_{\alpha +1})<\mathrm {lh}(E^{\mathcal {U}}_\alpha )$
. However,
$\mathrm {lh}(E^{\mathcal {U}}_{\alpha +1})<\mathrm {lh}(E^{\mathcal {U}}_\alpha )$
. However,
Now we claim that
![]() $E^{\mathcal {T}}_\alpha $
is also superstrong, and therefore
$E^{\mathcal {T}}_\alpha $
is also superstrong, and therefore
![]() $\nu (E^{\mathcal {T}}_\alpha )=\lambda (E^{\mathcal {T}}_\alpha )$
and
$\nu (E^{\mathcal {T}}_\alpha )=\lambda (E^{\mathcal {T}}_\alpha )$
and
![]() ${\nu (E^{\mathcal {U}}_\alpha )=\lambda (E^{\mathcal {U}}_\alpha )}$
, and then it follows that
${\nu (E^{\mathcal {U}}_\alpha )=\lambda (E^{\mathcal {U}}_\alpha )}$
, and then it follows that
as required for the monotone
![]() $\nu $
-condition.
$\nu $
-condition.
So suppose
![]() $E^{\mathcal {T}}_\alpha $
is not superstrong. So
$E^{\mathcal {T}}_\alpha $
is not superstrong. So
![]() $\nu (E^{\mathcal {T}}_\alpha )<\lambda (E^{\mathcal {T}}_\alpha )$
, so
$\nu (E^{\mathcal {T}}_\alpha )<\lambda (E^{\mathcal {T}}_\alpha )$
, so
which implies that
![]() $E^{\mathcal {T}}_\alpha =F(M^{\mathcal {T}}_\alpha )$
and
$E^{\mathcal {T}}_\alpha =F(M^{\mathcal {T}}_\alpha )$
and
![]() $\pi _\alpha $
is
$\pi _\alpha $
is
![]() $\nu $
-low. In particular,
$\nu $
-low. In particular,
![]() $\pi _\alpha $
is not
$\pi _\alpha $
is not
![]() $\mathrm {r}\Sigma _1$
-elementary, so is not a near
$\mathrm {r}\Sigma _1$
-elementary, so is not a near
![]() $0$
-embedding. Let
$0$
-embedding. Let
![]() $j=\mathrm {root}^{\mathcal {T}}_\alpha \in \{-1,0\}$
. By the proof that the copying construction propagates near embeddings (see [Reference Schimmerling and Steel4]),
$j=\mathrm {root}^{\mathcal {T}}_\alpha \in \{-1,0\}$
. By the proof that the copying construction propagates near embeddings (see [Reference Schimmerling and Steel4]),
![]() $(j,\alpha ]_{\mathcal {T}}$
does not drop in model, and so
$(j,\alpha ]_{\mathcal {T}}$
does not drop in model, and so
![]() $\bar {M},\bar {U}$
are active. But because
$\bar {M},\bar {U}$
are active. But because
![]() $\bar {U}=\mathrm {Ult}_{m-1}(\bar {M},\bar {E})$
and
$\bar {U}=\mathrm {Ult}_{m-1}(\bar {M},\bar {E})$
and
we have
![]() $\bar {\gamma }\neq \mathrm {cr}(F^{\bar {U}})$
, and then similarly, as
$\bar {\gamma }\neq \mathrm {cr}(F^{\bar {U}})$
, and then similarly, as
![]() $\bar {\theta }\leq \lambda (E^{\mathcal {T}}_0)$
, it easily follows that
$\bar {\theta }\leq \lambda (E^{\mathcal {T}}_0)$
, it easily follows that
![]() $j={-}1$
. But then
$j={-}1$
. But then
![]() $\mathrm {cr}(i^{\mathcal {T}}_{j\alpha })\leq \bar {\gamma }$
and
$\mathrm {cr}(i^{\mathcal {T}}_{j\alpha })\leq \bar {\gamma }$
and
![]() $\bar {\theta }\leq \lambda (E^{\mathcal {T}}_0)$
, so
$\bar {\theta }\leq \lambda (E^{\mathcal {T}}_0)$
, so
![]() $\bar {\gamma }\neq \mathrm {cr}(F(M^{\mathcal {T}}_\alpha ))$
, contradiction.
$\bar {\gamma }\neq \mathrm {cr}(F(M^{\mathcal {T}}_\alpha ))$
, contradiction.
So
![]() $\nu (E^{\mathcal {T}}_\alpha )\leq \nu (E^{\mathcal {T}}_{\alpha +1})$
, as desired. This is the only situation in which the monotone length condition can fail. We leave the remaining details of the lifting process to the reader.
$\nu (E^{\mathcal {T}}_\alpha )\leq \nu (E^{\mathcal {T}}_{\alpha +1})$
, as desired. This is the only situation in which the monotone length condition can fail. We leave the remaining details of the lifting process to the reader.
Case 2.
![]() $\pi "\bar {\theta }$
is unbounded in
$\pi "\bar {\theta }$
is unbounded in
![]() $\theta $
.
$\theta $
.
In this case we do not see how to produce a single map lifting
![]() $\bar {M}$
, and instead produce a sequence of maps. Note that
$\bar {M}$
, and instead produce a sequence of maps. Note that
![]() $\theta $
is a limit cardinal of M (by the case hypothesis we have an
$\theta $
is a limit cardinal of M (by the case hypothesis we have an ![]() -singularization of
-singularization of
![]() $\theta $
, and if
$\theta $
, and if
![]() $\theta =\gamma ^{+M}$
this routinely implies that
$\theta =\gamma ^{+M}$
this routinely implies that
![]() $\rho _m^M<\theta $
, a contradiction), and so
$\rho _m^M<\theta $
, a contradiction), and so
![]() $\bar {\theta }$
is a limit cardinal of
$\bar {\theta }$
is a limit cardinal of
![]() $\bar {M}$
. For each
$\bar {M}$
. For each
![]() $\bar {M}$
-cardinal
$\bar {M}$
-cardinal
![]() $\gamma <\bar {\theta }$
, let
$\gamma <\bar {\theta }$
, let
![]() $(M^{\prime }_\gamma ,\sigma _\gamma )$
be such that
$(M^{\prime }_\gamma ,\sigma _\gamma )$
be such that
![]() $M^{\prime }_\gamma \triangleleft M|\theta $
and
$M^{\prime }_\gamma \triangleleft M|\theta $
and
![]() $\sigma _\gamma :\bar {M}\to M^{\prime }_\gamma $
is a near
$\sigma _\gamma :\bar {M}\to M^{\prime }_\gamma $
is a near
![]() $(m-1)$
-embedding with
$(m-1)$
-embedding with
and
![]() $\rho _m^{M^{\prime }_\gamma }=\sigma _\gamma (\gamma )^{+M}$
; we get such pairs by taking appropriate hulls much as in the previous case.
$\rho _m^{M^{\prime }_\gamma }=\sigma _\gamma (\gamma )^{+M}$
; we get such pairs by taking appropriate hulls much as in the previous case.
Now for each
![]() $\gamma $
we have
$\gamma $
we have
![]() $M^{\prime }_\gamma \triangleleft U$
. So we can use
$M^{\prime }_\gamma \triangleleft U$
. So we can use
![]() $(\left <\sigma _\gamma \right>_{\gamma <\bar {\theta }},\psi )$
to lift trees on
$(\left <\sigma _\gamma \right>_{\gamma <\bar {\theta }},\psi )$
to lift trees on
![]() $\mathfrak {P}$
to m-maximal trees on U. This is much as in the previous case, but this time when
$\mathfrak {P}$
to m-maximal trees on U. This is much as in the previous case, but this time when
![]() $\mathrm {cr}(E^{\mathcal {T}}_\alpha )=\gamma <\bar {\theta }$
, then we define
$\mathrm {cr}(E^{\mathcal {T}}_\alpha )=\gamma <\bar {\theta }$
, then we define
![]() $Q_{\alpha +1}=i^{\mathcal {U}}_{0,\alpha +1}(M^{\prime }_\gamma )$
and define
$Q_{\alpha +1}=i^{\mathcal {U}}_{0,\alpha +1}(M^{\prime }_\gamma )$
and define
![]() $\pi _{\alpha +1}$
via the Shift Lemma from
$\pi _{\alpha +1}$
via the Shift Lemma from
![]() $\sigma _\gamma $
and
$\sigma _\gamma $
and
![]() $\pi _\alpha $
. We get the monotone length condition here, because
$\pi _\alpha $
. We get the monotone length condition here, because
![]() $\sigma _\gamma (\gamma )^{+}<\mathrm {Ord}^{M^{\prime }_\gamma }$
. The details are left to the reader.
$\sigma _\gamma (\gamma )^{+}<\mathrm {Ord}^{M^{\prime }_\gamma }$
. The details are left to the reader.
Using the claim, we can now complete the proof. We get a successful comparison
![]() $(\mathcal {T},\mathcal {U})$
of
$(\mathcal {T},\mathcal {U})$
of
![]() $(\bar {M},\mathfrak {P})$
, with
$(\bar {M},\mathfrak {P})$
, with
![]() $\mathcal {T}$
being
$\mathcal {T}$
being
![]() $(m-1)$
-maximal. Note that all extenders used in the comparison have length
$(m-1)$
-maximal. Note that all extenders used in the comparison have length
![]() $>\bar {\theta }$
. Standard fine structural arguments show that
$>\bar {\theta }$
. Standard fine structural arguments show that
![]() $b^{\mathcal {U}}$
is above
$b^{\mathcal {U}}$
is above
![]() $\bar {U}$
and
$\bar {U}$
and
![]() $b^{\mathcal {T}},b^{\mathcal {U}}$
are non-model-dropping,
$b^{\mathcal {T}},b^{\mathcal {U}}$
are non-model-dropping,
![]() $M^{\mathcal {T}}_\infty =Q=M^{\mathcal {U}}_\infty $
and
$M^{\mathcal {T}}_\infty =Q=M^{\mathcal {U}}_\infty $
and
![]() $\deg ^{\mathcal {T}}_\infty =m-1=\deg ^{\mathcal {U}}_\infty $
. So
$\deg ^{\mathcal {T}}_\infty =m-1=\deg ^{\mathcal {U}}_\infty $
. So
![]() $\bar {\theta }\leq \mathrm {cr}(i^{\mathcal {U}})$
, so
$\bar {\theta }\leq \mathrm {cr}(i^{\mathcal {U}})$
, so
![]() $\bar {U}|\bar {\theta }^{+\bar {U}}=Q|\bar {\theta }^{+Q}$
, and since
$\bar {U}|\bar {\theta }^{+\bar {U}}=Q|\bar {\theta }^{+Q}$
, and since
![]() $\mathrm {lh}(E^{\mathcal {T}}_0)>\bar {\theta }$
, therefore
$\mathrm {lh}(E^{\mathcal {T}}_0)>\bar {\theta }$
, therefore
But if
![]() $\bar {\theta }<\bar {\tau }$
then because
$\bar {\theta }<\bar {\tau }$
then because
![]() $\mathcal {H}_{\bar {\tau }}^{\bar {M}}\subseteq \bar {U}$
, it follows that
$\mathcal {H}_{\bar {\tau }}^{\bar {M}}\subseteq \bar {U}$
, it follows that
![]() $\bar {U}|\bar {\theta }^{+\bar {U}}=\bar {M}|\bar {\theta }^{+\bar {M}}$
, which contradicts the choice of
$\bar {U}|\bar {\theta }^{+\bar {U}}=\bar {M}|\bar {\theta }^{+\bar {M}}$
, which contradicts the choice of
![]() $\bar {\theta }$
. So
$\bar {\theta }$
. So
![]() $\bar {\theta }=\bar {\tau }$
, which with line (4) gives the statement of conclusion (i) of the theorem but with
$\bar {\theta }=\bar {\tau }$
, which with line (4) gives the statement of conclusion (i) of the theorem but with
![]() $\bar {M}$
instead of N. However, this statement is preserved by
$\bar {M}$
instead of N. However, this statement is preserved by
![]() $\pi ,\pi _{MR}$
, so part (i) for N follows.
$\pi ,\pi _{MR}$
, so part (i) for N follows.
Assuming also that
![]() $\ell =0$
, so
$\ell =0$
, so
![]() $\bar {E}$
is generated by
$\bar {E}$
is generated by
![]() $\bar {\tau }$
, then standard arguments show that
$\bar {\tau }$
, then standard arguments show that
![]() $\bar {E}$
is just the
$\bar {E}$
is just the
![]() $(\bar {\kappa },\bar {\tau })$
-extender derived from
$(\bar {\kappa },\bar {\tau })$
-extender derived from
![]() $i^{\mathcal {T}}$
, and therefore that in fact
$i^{\mathcal {T}}$
, and therefore that in fact
![]() $\bar {E}\in \mathbb {E}^{\bar {M}}$
. But this reflects back to N, giving part (ii).
$\bar {E}\in \mathbb {E}^{\bar {M}}$
. But this reflects back to N, giving part (ii).
Proof of Theorems 1.2 and 1.4
Theorem 2.12 directly implies 1.2. For 1.4 note that we may replace the given extender with a sub-extender derived from a set of form
![]() $\tau \cup t$
, where t is a finite set of ordinals, and then appeal to 2.12.
$\tau \cup t$
, where t is a finite set of ordinals, and then appeal to 2.12.
From 1.2 we immediately get:
Corollary 2.13. Let N be a
![]() $(0,\omega _1+1)$
-iterable premouse and
$(0,\omega _1+1)$
-iterable premouse and
![]() $\mu ,\delta ,\kappa \in N$
. Then
$\mu ,\delta ,\kappa \in N$
. Then
![]() $:$
$:$
-
– If
 $N\models $
“
$N\models $
“
 $\mu $
is a normal measure” then
$\mu $
is a normal measure” then
 $\mu \in \mathbb {E}^N$
.
$\mu \in \mathbb {E}^N$
. -
– If
 $N\models $
“
$N\models $
“
 $\delta $
is Woodin” then
$\delta $
is Woodin” then
 $N\models $
“
$N\models $
“
 $\delta $
is Woodin via extenders in
$\delta $
is Woodin via extenders in
 $\mathbb {E}^N$
”.
$\mathbb {E}^N$
”. -
– If
 $N\models \mathrm {PS}+$
“
$N\models \mathrm {PS}+$
“
 $\kappa $
is strong” then
$\kappa $
is strong” then
 $N\models $
“
$N\models $
“
 $\kappa $
is strong via extenders in
$\kappa $
is strong via extenders in
 $\mathbb {E}^N$
”.
$\mathbb {E}^N$
”.
We next prove a finer variant of Theorem 2.12. However, we do not actually need the variant in later sections of the paper.
Recall the Dodd projectum and parameter
![]() $\tau _E$
and
$\tau _E$
and
![]() $t_E$
of a short extender E (see [Reference Schimmerling3] or [Reference Schlutzenberg11, Section 2] for background). The most important fact we use in this section regarding this notion is the following:
$t_E$
of a short extender E (see [Reference Schimmerling3] or [Reference Schlutzenberg11, Section 2] for background). The most important fact we use in this section regarding this notion is the following:
Fact 2.14 (Steel).
Let M be a
![]() $1$
-sound,
$1$
-sound,
![]() $(0,\omega _1+1)$
-iterable premouse which is below superstrong. Then every
$(0,\omega _1+1)$
-iterable premouse which is below superstrong. Then every
![]() $E\in \mathbb {E}_+^M$
is Dodd-sound.
$E\in \mathbb {E}_+^M$
is Dodd-sound.
Remark 2.15. Note that 2.14 and all results in this paper are for mice with Mitchell–Steel indexing. A theorem analogous to 2.14 has been proven by Zeman for mice with Jensen indexing, without the superstrong restriction (see [Reference Zeman15]). Further, 2.14 has also been generalized for mice in Mitchell–Steel indexing, to allow extenders of superstrong type in
![]() $\mathbb {E}_+^M$
(see [Reference Schlutzenberg7]).Footnote
9
With this, Theorem 2.17 should also generalize accordingly in a straightforward manner. However, as of at the time of publication of this paper, [Reference Schlutzenberg7] is only at the preprint stage, so we have only formally stated 2.17 “below superstrong”.
$\mathbb {E}_+^M$
(see [Reference Schlutzenberg7]).Footnote
9
With this, Theorem 2.17 should also generalize accordingly in a straightforward manner. However, as of at the time of publication of this paper, [Reference Schlutzenberg7] is only at the preprint stage, so we have only formally stated 2.17 “below superstrong”.
Note that in 2.17, we allow E itself to ostensibly be of “superstrong type”, but then it follows that
![]() $t=\emptyset $
and
$t=\emptyset $
and
![]() $E\in \mathbb {E}_+^M$
, so in fact, E is not of such type (because M is assumed to be below superstrong).
$E\in \mathbb {E}_+^M$
, so in fact, E is not of such type (because M is assumed to be below superstrong).
Definition 2.16. Let M be a premouse and E a standard short M-extender, with support
![]() $\tau +\ell $
where
$\tau +\ell $
where
![]() $\tau $
is a limit ordinal and
$\tau $
is a limit ordinal and
![]() $\ell <\omega $
. Suppose E is weakly amenable (to M). Let
$\ell <\omega $
. Suppose E is weakly amenable (to M). Let
![]() $U=\mathrm {Ult}_0(M,E)$
(we don’t assume U is wellfounded). Let
$U=\mathrm {Ult}_0(M,E)$
(we don’t assume U is wellfounded). Let
![]() $\kappa =\mathrm {cr}(E)$
. We say that E is amenably
$\kappa =\mathrm {cr}(E)$
. We say that E is amenably ![]() iff
iff
![]() $\tau <\rho _0^M$
and
$\tau <\rho _0^M$
and
![]() $\tau ^{+U}$
is wellfounded and
$\tau ^{+U}$
is wellfounded and
![]() $U|\tau ^{+U}\subseteq M$
, and the standard coding of E as an amenable subset of
$U|\tau ^{+U}\subseteq M$
, and the standard coding of E as an amenable subset of
![]() $U|\tau ^{+U}$
is
$U|\tau ^{+U}$
is ![]() . Here the coding consists of tuples
. Here the coding consists of tuples
![]() $(\xi ,\alpha _\xi ,E_\xi ),$
where
$(\xi ,\alpha _\xi ,E_\xi ),$
where
![]() $\xi <\kappa ^{+M}$
and
$\xi <\kappa ^{+M}$
and
![]() $E_\xi $
is the natural coding of the extender fragment
$E_\xi $
is the natural coding of the extender fragment
as a subset of
![]() $M|\tau $
, and
$M|\tau $
, and
![]() $\alpha _\xi $
is the least
$\alpha _\xi $
is the least
![]() $\alpha $
such that
$\alpha $
such that
![]() $E_\xi \in U|(\alpha _\xi +\omega )$
. (By the usual proof (see [Reference Mitchell and Steel1, Section 2]),
$E_\xi \in U|(\alpha _\xi +\omega )$
. (By the usual proof (see [Reference Mitchell and Steel1, Section 2]),
![]() $E_\xi \in U$
and the
$E_\xi \in U$
and the
![]() $\alpha _\xi $
’s are cofinal in
$\alpha _\xi $
’s are cofinal in
![]() $\tau ^{+U}$
.) We say that E is explicitly Dodd-solid above
$\tau ^{+U}$
.) We say that E is explicitly Dodd-solid above
![]() $\tau $
iff, letting
$\tau $
iff, letting
![]() $j:M\to U$
be the ultrapower map and
$j:M\to U$
be the ultrapower map and
we have
![]() $E_j\!\upharpoonright \!(\alpha \cup (t\backslash \{\alpha \}))\in U$
for each
$E_j\!\upharpoonright \!(\alpha \cup (t\backslash \{\alpha \}))\in U$
for each
![]() $\alpha \in t$
.
$\alpha \in t$
.
Theorem 2.17. Let
![]() $m<\omega $
and let M be an
$m<\omega $
and let M be an
![]() $(m+1)$
-sound,
$(m+1)$
-sound,
![]() $(m,\omega _1+1)$
-iterable premouse which is below superstrong. Let E be a standard short
$(m,\omega _1+1)$
-iterable premouse which is below superstrong. Let E be a standard short
![]() $M^{\mathrm {sq}}$
-extender, with support
$M^{\mathrm {sq}}$
-extender, with support
![]() $\tau +\ell $
where
$\tau +\ell $
where
![]() $\tau $
is a limit ordinal and
$\tau $
is a limit ordinal and
![]() $\ell <\omega $
. Suppose E is weakly amenable to M,
$\ell <\omega $
. Suppose E is weakly amenable to M,
![]() $\kappa =\mathrm {cr}(E)<\rho _{m}^M$
, E is amenably
$\kappa =\mathrm {cr}(E)<\rho _{m}^M$
, E is amenably ![]() ,
,
![]() $\tau \leq \rho _{m+1}^M$
and
$\tau \leq \rho _{m+1}^M$
and
![]() $\tau $
is an M-cardinal with
$\tau $
is an M-cardinal with
![]() $\mathcal {H}_\tau ^M\subseteq U$
, where
$\mathcal {H}_\tau ^M\subseteq U$
, where
![]() $U=\mathrm {Ult}_m(M,E)$
. Then
$U=\mathrm {Ult}_m(M,E)$
. Then
![]() $:$
$:$
-
(i)
 $U|\tau ^{+U}=M||\tau ^{+U}$
and
$U|\tau ^{+U}=M||\tau ^{+U}$
and -
(ii) if E is explicitly Dodd-solid above
 $\tau $
then
$\tau $
then
 $E\in \mathbb {E}_+^M$
.
$E\in \mathbb {E}_+^M$
.
Proof Let
![]() $j:M\to U$
be the ultrapower map. Let t be as in Definition 2.16. So
$j:M\to U$
be the ultrapower map. Let t be as in Definition 2.16. So
![]() $E\equiv E_j\!\upharpoonright \!\tau \cup t$
, and we will identify these two extenders in what follows.
$E\equiv E_j\!\upharpoonright \!\tau \cup t$
, and we will identify these two extenders in what follows.
If
![]() $U||\tau =M||\tau $
then let
$U||\tau =M||\tau $
then let
![]() $\theta =\tau $
, and otherwise let
$\theta =\tau $
, and otherwise let
![]() $\lambda $
be least such that
$\lambda $
be least such that
![]() $U|\lambda \neq M|\lambda $
and let
$U|\lambda \neq M|\lambda $
and let
![]() $\theta =\mathrm {card}^M(\lambda )$
. So
$\theta =\mathrm {card}^M(\lambda )$
. So
![]() $\theta $
is an M-cardinal and
$\theta $
is an M-cardinal and
![]() $\theta \leq \tau $
, and by condensation and weak amenability,
$\theta \leq \tau $
, and by condensation and weak amenability,
![]() $\kappa ^{+M}=\kappa ^{+U} \leq \theta $
. Note that if E is explicitly Dodd-solid above
$\kappa ^{+M}=\kappa ^{+U} \leq \theta $
. Note that if E is explicitly Dodd-solid above
![]() $\tau $
then E is Dodd-sound. (For suppose
$\tau $
then E is Dodd-sound. (For suppose
![]() $\kappa ^{+M}<\tau $
. As
$\kappa ^{+M}<\tau $
. As
![]() $E\!\upharpoonright \!(\tau \cup t)$
is amenably
$E\!\upharpoonright \!(\tau \cup t)$
is amenably ![]() and
and
![]() $\tau \leq \rho _{m+1}^M$
, then
$\tau \leq \rho _{m+1}^M$
, then
![]() $E\!\upharpoonright \!(\alpha \cup t)\in M$
for each
$E\!\upharpoonright \!(\alpha \cup t)\in M$
for each
![]() $\alpha <\tau $
. But
$\alpha <\tau $
. But
![]() $\mathcal {H}_\tau ^M\subseteq U$
, so
$\mathcal {H}_\tau ^M\subseteq U$
, so
![]() $E\!\upharpoonright \!(\alpha \cup t)\in U$
.) Let
$E\!\upharpoonright \!(\alpha \cup t)\in U$
.) Let
![]() $e\in [\mathfrak {C}_0(M)]^{<\omega }$
be such that:
$e\in [\mathfrak {C}_0(M)]^{<\omega }$
be such that:
-
1.
 $\theta ,\tau \in e$
(recall that
$\theta ,\tau \in e$
(recall that
 $\tau <\rho _0^M$
by 2.16).
$\tau <\rho _0^M$
by 2.16). -
2. If
 $\mathfrak {C}_0(M)$
has largest cardinal
$\mathfrak {C}_0(M)$
has largest cardinal
 $\Omega $
then
$\Omega $
then
 $\Omega \in e$
.
$\Omega \in e$
. -
3. The amenable coding of
 $E\!\upharpoonright \!(\tau \cup t)$
(described in 2.16) is
$E\!\upharpoonright \!(\tau \cup t)$
(described in 2.16) is
 $\mathrm {r}\Sigma _{m+1}^M(\{e\})$
.
$\mathrm {r}\Sigma _{m+1}^M(\{e\})$
. -
4. If
 $\theta <\tau $
then
$\theta <\tau $
then
 $\chi \in e$
where
$\chi \in e$
where
 $\chi <\tau $
is least such that
$\chi <\tau $
is least such that
 $U|\chi \neq M|\chi $
.
$U|\chi \neq M|\chi $
. -
5. If
 $\tau ^{+U}<\tau ^{+M}$
then
$\tau ^{+U}<\tau ^{+M}$
then
 $\tau ^{+U}\in e$
.
$\tau ^{+U}\in e$
. -
6. If
 $\tau ^{+U}=\tau ^{+M}$
but
$\tau ^{+U}=\tau ^{+M}$
but
 $U|\tau ^{+U}\neq M||\tau ^{+M}$
then
$U|\tau ^{+U}\neq M||\tau ^{+M}$
then
 $\lambda \in e$
where
$\lambda \in e$
where
 $\lambda \in (\tau ,\tau ^{+U}]$
is least such that
$\lambda \in (\tau ,\tau ^{+U}]$
is least such that
 $U|\lambda \neq M|\lambda $
(note that in fact,
$U|\lambda \neq M|\lambda $
(note that in fact,
 $\lambda <\tau ^{+U}$
, because
$\lambda <\tau ^{+U}$
, because
 $\tau ^{+U}<\mathrm {Ord}^U$
, because
$\tau ^{+U}<\mathrm {Ord}^U$
, because
 $\kappa ^{+M}\leq \tau <\rho _0^M$
).
$\kappa ^{+M}\leq \tau <\rho _0^M$
). -
7. If E is explicitly Dodd-solid above
 $\tau $
then there are
$\tau $
then there are
 $a,f\in e$
such that
$a,f\in e$
such that
 $a\in [\tau ]^{<\omega }$
and
$a\in [\tau ]^{<\omega }$
and
 $[a\cup t,f]^{M,m}_E$
is the (finite) set of Dodd-solidity witnesses (for t).
$[a\cup t,f]^{M,m}_E$
is the (finite) set of Dodd-solidity witnesses (for t). -
8. Footnote 10 If E is explicitly Dodd-solid above
 $\tau $
and
$\tau $
and
 $\theta =\tau $
and and
$\theta =\tau $
and and $$\begin{align*}\varsigma=\tau^{+U}<\tau^{+M} \end{align*}$$
$$\begin{align*}\varsigma=\tau^{+U}<\tau^{+M} \end{align*}$$
 $U|\varsigma =M||\varsigma $
but
$U|\varsigma =M||\varsigma $
but
 $M|\varsigma $
is active with an extender F such that
$M|\varsigma $
is active with an extender F such that
 $\kappa <\mathrm {cr}(F)$
, then there are
$\kappa <\mathrm {cr}(F)$
, then there are
 $a,f\in e$
with
$a,f\in e$
with
 $a\in [\tau ]^{<\omega }$
and such that
$a\in [\tau ]^{<\omega }$
and such that  $$\begin{align*}[a\cup t,f]^{M,m}_E=E\!\upharpoonright\!(\mathrm{cr}(F)\cup t).\end{align*}$$
$$\begin{align*}[a\cup t,f]^{M,m}_E=E\!\upharpoonright\!(\mathrm{cr}(F)\cup t).\end{align*}$$
Let q be such that
![]() $(\omega ,q)$
is
$(\omega ,q)$
is
![]() $(m+1)$
-self-solid for M and
$(m+1)$
-self-solid for M and
![]() $e\in \mathrm {rg}(\pi ),$
where
$e\in \mathrm {rg}(\pi ),$
where
![]() ${{\bar {M}}=\mathrm {cHull}_{m+1}^M(\{\vec {p}_m^M,q\})}$
and
${{\bar {M}}=\mathrm {cHull}_{m+1}^M(\{\vec {p}_m^M,q\})}$
and
![]() $\pi :{\bar {M}}\to M$
is the uncollapse (q exists by 2.3).
$\pi :{\bar {M}}\to M$
is the uncollapse (q exists by 2.3).
Let
![]() $\pi ({\bar {q}})=q$
,
$\pi ({\bar {q}})=q$
,
![]() $\pi ({\bar {\theta }})=\theta $
, etc. Also write
$\pi ({\bar {\theta }})=\theta $
, etc. Also write
![]() ${\bar {t}}$
for the preimage of t “in the codes”; but note we did not demand that
${\bar {t}}$
for the preimage of t “in the codes”; but note we did not demand that
![]() $t\subseteq \mathrm {Ord}^M$
. So
$t\subseteq \mathrm {Ord}^M$
. So
![]() ${\bar {M}}$
is
${\bar {M}}$
is
![]() $(m+1)$
-sound with
$(m+1)$
-sound with
![]() $\rho _{m+1}^{\bar {M}}=\omega $
and
$\rho _{m+1}^{\bar {M}}=\omega $
and
![]() ${\bar {q}}=p_{m+1}^{{\bar {M}}}$
. Let
${\bar {q}}=p_{m+1}^{{\bar {M}}}$
. Let
![]() ${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$
be defined over
${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$
be defined over
![]() ${\bar {M}}$
from
${\bar {M}}$
from
![]() ${\bar {e}}$
as
${\bar {e}}$
as
![]() $E\!\upharpoonright \!\tau \cup t$
is defined over M from e. Then the usual proof that
$E\!\upharpoonright \!\tau \cup t$
is defined over M from e. Then the usual proof that
![]() $\Sigma _1$
-substructures of premice are premiceFootnote
11
and some similar considerations show that most of the facts reflect to
$\Sigma _1$
-substructures of premice are premiceFootnote
11
and some similar considerations show that most of the facts reflect to
![]() ${\bar {M}},{\bar {E}}$
, etc., and in particular:
${\bar {M}},{\bar {E}}$
, etc., and in particular:
-
1’.
 ${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$
is a weakly amenable short
${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$
is a weakly amenable short
 ${\bar {M}}$
-extender with
${\bar {M}}$
-extender with
 ${\bar {\kappa }}=\mathrm {cr}({\bar {E}})<\rho _m^{\bar {M}}$
.
${\bar {\kappa }}=\mathrm {cr}({\bar {E}})<\rho _m^{\bar {M}}$
.
Let
![]() ${\bar {E}}$
be the short
${\bar {E}}$
be the short
![]() $\bar {M}$
-extender generated by
$\bar {M}$
-extender generated by
![]() ${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$
and let
${\bar {E}}\!\upharpoonright \!{\bar {\tau }}\cup {\bar {t}}$
and let
-
2’. If M has largest cardinal
 $\Omega $
then
$\Omega $
then
 ${\bar {M}}$
has largest cardinal
${\bar {M}}$
has largest cardinal
 $\bar {\Omega }$
.
$\bar {\Omega }$
. -
3’.
 ${\bar {\theta }},{\bar {\tau }}$
are
${\bar {\theta }},{\bar {\tau }}$
are
 ${\bar {M}}$
-cardinals,
${\bar {M}}$
-cardinals,
 $\mathcal {H}^{\bar {M}}_{{\bar {\tau }}}\subseteq {\bar {U}}$
and
$\mathcal {H}^{\bar {M}}_{{\bar {\tau }}}\subseteq {\bar {U}}$
and
 ${\bar {M}}|{\bar {\theta }}={\bar {U}}|{\bar {\theta }}$
.
${\bar {M}}|{\bar {\theta }}={\bar {U}}|{\bar {\theta }}$
. -
4’. If
 $\theta <\tau $
then
$\theta <\tau $
then
 ${\bar {M}}|{\bar {\theta }}^{+{\bar {M}}}\neq {\bar {U}}|{\bar {\theta }}^{+{\bar {U}}}$
, and
${\bar {M}}|{\bar {\theta }}^{+{\bar {M}}}\neq {\bar {U}}|{\bar {\theta }}^{+{\bar {U}}}$
, and
 $\bar {\chi }$
is least such that
$\bar {\chi }$
is least such that
 ${\bar {M}}|\bar {\chi }\neq {\bar {U}}|\bar {\chi }$
.
${\bar {M}}|\bar {\chi }\neq {\bar {U}}|\bar {\chi }$
. -
5’. If
 $\theta =\tau $
then:
$\theta =\tau $
then:-
– If
 $\tau ^{+U}<\tau ^{+M}$
then
$\tau ^{+U}<\tau ^{+M}$
then
 ${\bar {\tau }}^{+{\bar {U}}}<{\bar {\tau }}^{+{\bar {M}}}$
and
${\bar {\tau }}^{+{\bar {U}}}<{\bar {\tau }}^{+{\bar {M}}}$
and
 $\pi ({\bar {\tau }}^{+{\bar {U}}})=\tau ^{+U}$
.
$\pi ({\bar {\tau }}^{+{\bar {U}}})=\tau ^{+U}$
. -
– If
 $\tau ^{+U}=\tau ^{+M}$
then
$\tau ^{+U}=\tau ^{+M}$
then
 ${\bar {\tau }}^{+{\bar {U}}}={\bar {\tau }}^{+{\bar {M}}}$
.
${\bar {\tau }}^{+{\bar {U}}}={\bar {\tau }}^{+{\bar {M}}}$
.
-
-
6’. If
 $\theta =\tau $
then:
$\theta =\tau $
then:-
– If
 $U|\tau ^{+U}=M||\tau ^{+U}$
then
$U|\tau ^{+U}=M||\tau ^{+U}$
then
 ${\bar {U}}|{\bar {\tau }}^{+{\bar {U}}}={\bar {M}}||{\bar {\tau }}^{+{\bar {U}}}$
.
${\bar {U}}|{\bar {\tau }}^{+{\bar {U}}}={\bar {M}}||{\bar {\tau }}^{+{\bar {U}}}$
. -
– If
 $U|\tau ^{+U}\neq M||\tau ^{+U}$
then
$U|\tau ^{+U}\neq M||\tau ^{+U}$
then
 ${\bar {\tau }}<\bar {\lambda }<{\bar {\tau }}^{+{\bar {U}}}$
and
${\bar {\tau }}<\bar {\lambda }<{\bar {\tau }}^{+{\bar {U}}}$
and
 $\bar {\lambda }$
is least such that
$\bar {\lambda }$
is least such that
 ${\bar {U}}|\bar {\lambda }\neq {\bar {M}}|\bar {\lambda }$
.
${\bar {U}}|\bar {\lambda }\neq {\bar {M}}|\bar {\lambda }$
.
-
-
7’. If E is explicitly Dodd-solid above
 $\tau $
then
$\tau $
then
 ${\bar {E}}$
is Dodd-solid with respect to
${\bar {E}}$
is Dodd-solid with respect to
 ${\bar {t}}$
. That is, for each
${\bar {t}}$
. That is, for each
 $\alpha \in {\bar {t}}$
, we have
$\alpha \in {\bar {t}}$
, we have
 ${\bar {E}}\!\upharpoonright \!(\alpha \cup ({\bar {t}}\backslash (\alpha +1)))\in {\bar {U}}$
.
${\bar {E}}\!\upharpoonright \!(\alpha \cup ({\bar {t}}\backslash (\alpha +1)))\in {\bar {U}}$
. -
8’. If E is explicitly Dodd-solid above
 $\tau $
and
$\tau $
and
 $U,M,\varsigma ,F$
are as in condition 8, then
$U,M,\varsigma ,F$
are as in condition 8, then
 $\bar {\varsigma }={\bar {\tau }}^{+{\bar {U}}}$
and
$\bar {\varsigma }={\bar {\tau }}^{+{\bar {U}}}$
and
 ${\bar {M}}|\bar {\varsigma }$
is active with
${\bar {M}}|\bar {\varsigma }$
is active with
 ${\bar {F}}$
and the Dodd-soundness witness
${\bar {F}}$
and the Dodd-soundness witness
 ${\bar {E}}\!\upharpoonright \!(\mathrm {cr}({\bar {F}})\cup {\bar {t}})$
is in
${\bar {E}}\!\upharpoonright \!(\mathrm {cr}({\bar {F}})\cup {\bar {t}})$
is in
 ${\bar {U}}$
.
${\bar {U}}$
.
(We do not yet know that
![]() ${\bar {U}}$
is wellfounded.) Let
${\bar {U}}$
is wellfounded.) Let
![]() ${\bar {j}}:{\bar {M}}\to {\bar {U}}$
be the ultrapower map. Let
${\bar {j}}:{\bar {M}}\to {\bar {U}}$
be the ultrapower map. Let
![]() $\psi :{\bar {U}}\to U$
be the Shift Lemma map. Define the phalanx
$\psi :{\bar {U}}\to U$
be the Shift Lemma map. Define the phalanx
![]() $\mathfrak {P}=(({\bar {M}},m,{\bar {\theta }}), ({\bar {U}},m), {\bar {\theta }})$
.
$\mathfrak {P}=(({\bar {M}},m,{\bar {\theta }}), ({\bar {U}},m), {\bar {\theta }})$
.
Claim 1.
![]() ${\bar {U}}$
is wellfounded and
${\bar {U}}$
is wellfounded and
![]() $\mathfrak {P}$
is
$\mathfrak {P}$
is
![]() $(\omega _1+1)$
-iterable.
$(\omega _1+1)$
-iterable.
Proof The argument is mostly similar to that in the proof of 2.12. We will lift m-maximal trees
![]() $\mathcal {T}$
on
$\mathcal {T}$
on
![]() $\mathfrak {P}$
to m-maximal trees on M.Footnote
12
For this we will find embeddings from
$\mathfrak {P}$
to m-maximal trees on M.Footnote
12
For this we will find embeddings from
![]() ${\bar {M}}$
and
${\bar {M}}$
and
![]() ${\bar {U}}$
into segments of M with appropriate agreement. As before, in one case we only see how to find an infinite sequence of embeddings from
${\bar {U}}$
into segments of M with appropriate agreement. As before, in one case we only see how to find an infinite sequence of embeddings from
![]() $\bar {M}$
into various segments of M, and use of all these together as base copy maps. We will initially find such a system of maps inside U, and then deduce that there is also such a system in M via the elementarity of j. We first make some general observations that will lead to finding the system of embeddings in U.
$\bar {M}$
into various segments of M, and use of all these together as base copy maps. We will initially find such a system of maps inside U, and then deduce that there is also such a system in M via the elementarity of j. We first make some general observations that will lead to finding the system of embeddings in U.
Let
![]() $R\triangleleft M$
. Note that M satisfies condensation with respect to premice embedded into R; in particular,
$R\triangleleft M$
. Note that M satisfies condensation with respect to premice embedded into R; in particular,
![]() $M\models $
“For every
$M\models $
“For every
![]() $s<\omega $
and every premouse
$s<\omega $
and every premouse
![]() $S\in R$
such that S is
$S\in R$
such that S is
![]() $(s+1)$
-sound and
$(s+1)$
-sound and
![]() $\pi :S\to R$
is s-lifting and and
$\pi :S\to R$
is s-lifting and and
![]() $\mathrm {cr}(\pi )\geq \rho _{s+1}^S$
, either (i)
$\mathrm {cr}(\pi )\geq \rho _{s+1}^S$
, either (i)
![]() $S\triangleleft R$
or (ii)
$S\triangleleft R$
or (ii)
![]() $\alpha =_{\mathrm {def}}\mathrm {cr}(\pi )=\rho _{s+1}^S$
and
$\alpha =_{\mathrm {def}}\mathrm {cr}(\pi )=\rho _{s+1}^S$
and
![]() $R|\alpha $
is active and
$R|\alpha $
is active and
![]() $S\triangleleft \mathrm {Ult}_0(R|\alpha ,F^{R|\alpha })$
”. Therefore U satisfies the same statement regarding its proper segments.
$S\triangleleft \mathrm {Ult}_0(R|\alpha ,F^{R|\alpha })$
”. Therefore U satisfies the same statement regarding its proper segments.
Let
![]() $M_\kappa =\mathrm {cHull}_{m+1}^M(\kappa \cup \{q\})$
. Let
$M_\kappa =\mathrm {cHull}_{m+1}^M(\kappa \cup \{q\})$
. Let
![]() $\sigma _\kappa :{\bar {M}}\to M_\kappa $
and
$\sigma _\kappa :{\bar {M}}\to M_\kappa $
and
![]() $\pi _\kappa :M_\kappa \to M$
be the natural maps and
$\pi _\kappa :M_\kappa \to M$
be the natural maps and
![]() $\pi _\kappa (q_\kappa )=q$
. Note that
$\pi _\kappa (q_\kappa )=q$
. Note that
![]() $M_\kappa $
is sound and
$M_\kappa $
is sound and
![]() $M_\kappa \in M$
. So
$M_\kappa \in M$
. So
![]() $\rho _{m+1}^{M_\kappa }=\kappa \leq \mathrm {cr}(\pi _\kappa )$
. By condensation,
$\rho _{m+1}^{M_\kappa }=\kappa \leq \mathrm {cr}(\pi _\kappa )$
. By condensation,
![]() $M_\kappa \triangleleft M$
.
$M_\kappa \triangleleft M$
.
Now
![]() $\tau $
is a U-cardinal with
$\tau $
is a U-cardinal with
![]() $\kappa <\tau \leq j(\kappa )$
. Working in U, let
$\kappa <\tau \leq j(\kappa )$
. Working in U, let
with
![]() $r\in [\mathrm {Ord}^{j(M_\kappa)}]^{<\omega }$
chosen such that
$r\in [\mathrm {Ord}^{j(M_\kappa)}]^{<\omega }$
chosen such that
![]() $U\models $
“
$U\models $
“
![]() $(\tau ,r)$
is
$(\tau ,r)$
is
![]() $(m+1)$
-self-solid for
$(m+1)$
-self-solid for
![]() $j(M_\kappa )$
and letting
$j(M_\kappa )$
and letting
![]() $\varrho _\tau :U'\to j(M_\kappa )$
be the uncollapse, then
$\varrho _\tau :U'\to j(M_\kappa )$
be the uncollapse, then
![]() $j(q_\kappa ),t\in \mathrm {rg}(\varrho _\tau )$
”. Such an r exists by the elementarity of j and by 2.3. (Note that
$j(q_\kappa ),t\in \mathrm {rg}(\varrho _\tau )$
”. Such an r exists by the elementarity of j and by 2.3. (Note that
![]() $U\models $
“
$U\models $
“
![]() $j(M_\kappa )$
is wellfounded”; the transitive collapse
$j(M_\kappa )$
is wellfounded”; the transitive collapse
![]() $U'$
is computed inside U, where it is well-defined.) Note that if
$U'$
is computed inside U, where it is well-defined.) Note that if
![]() $\tau =j(\kappa )$
then
$\tau =j(\kappa )$
then
![]() $t=\emptyset $
and
$t=\emptyset $
and
![]() $U'=j(M_\kappa )$
and
$U'=j(M_\kappa )$
and
![]() $r=j(q_\kappa )$
. And if
$r=j(q_\kappa )$
. And if
![]() $\tau <j(\kappa )$
then
$\tau <j(\kappa )$
then
![]() $\rho _{m+1}^{U'}=\tau $
, so
$\rho _{m+1}^{U'}=\tau $
, so
![]() $U'\triangleleft j(M_\kappa )$
by condensation in U. In fact,
$U'\triangleleft j(M_\kappa )$
by condensation in U. In fact,
![]() $U'\triangleleft U|\tau ^{+U}$
, and we assumed that
$U'\triangleleft U|\tau ^{+U}$
, and we assumed that
![]() $U|\tau ^{+U}$
is wellfounded, so
$U|\tau ^{+U}$
is wellfounded, so
![]() $U'$
is wellfounded.
$U'$
is wellfounded.
Let
![]() $\psi :{\bar {U}}\to j(M_\kappa )$
be the Shift Lemma map induced by
$\psi :{\bar {U}}\to j(M_\kappa )$
be the Shift Lemma map induced by
![]() $\sigma _\kappa $
and
$\sigma _\kappa $
and
![]() $\pi $
. That is, givenFootnote
13
$\pi $
. That is, givenFootnote
13
where
![]() $\tau $
is an
$\tau $
is an
![]() $\mathrm {r}\Sigma _m$
term,
$\mathrm {r}\Sigma _m$
term,
![]() $z\in \mathfrak {C}_0({\bar {M}})$
and
$z\in \mathfrak {C}_0({\bar {M}})$
and
![]() $a\in [\bar {\tau }]^{<\omega }$
, thenFootnote
14
$a\in [\bar {\tau }]^{<\omega }$
, thenFootnote
14
 $$ \begin{align*} \psi(x)&=[\pi(a)\cup t,f^{M_\kappa}_{\tau,\sigma_\kappa(z)}]^{M,m}_E\\ &=j(f^{M_\kappa}_{\tau,\sigma_\kappa(z)})(\pi(a)\cup t)\\ &=(\tau^{j(M_\kappa)}(j(\sigma_\kappa(z)),\pi(a)\cup t))^U.\end{align*} $$
$$ \begin{align*} \psi(x)&=[\pi(a)\cup t,f^{M_\kappa}_{\tau,\sigma_\kappa(z)}]^{M,m}_E\\ &=j(f^{M_\kappa}_{\tau,\sigma_\kappa(z)})(\pi(a)\cup t)\\ &=(\tau^{j(M_\kappa)}(j(\sigma_\kappa(z)),\pi(a)\cup t))^U.\end{align*} $$
Now
![]() $\mathrm {rg}(\psi )\subseteq \mathrm {rg}(\varrho _\tau )$
, for given x, etc. as above, we have
$\mathrm {rg}(\psi )\subseteq \mathrm {rg}(\varrho _\tau )$
, for given x, etc. as above, we have
![]() $\pi (a)\subseteq \tau \subseteq \mathrm {rg}(\varrho _\tau )$
,
$\pi (a)\subseteq \tau \subseteq \mathrm {rg}(\varrho _\tau )$
,
![]() ${t\in \mathrm {rg}(\varrho _\tau )}$
, and
${t\in \mathrm {rg}(\varrho _\tau )}$
, and
![]() $j(\sigma _\kappa (z))\in \mathrm {rg}(\varrho _\tau )$
since
$j(\sigma _\kappa (z))\in \mathrm {rg}(\varrho _\tau )$
since
and
![]() $j(q_\kappa )\in \mathrm {rg}(\varrho _\tau )$
. So
$j(q_\kappa )\in \mathrm {rg}(\varrho _\tau )$
. So
![]() $\psi (x)\in \mathrm {rg}(\varrho _\tau )$
.
$\psi (x)\in \mathrm {rg}(\varrho _\tau )$
.
So we can define
![]() $\psi ':{\bar {U}}\to U'$
by
$\psi ':{\bar {U}}\to U'$
by
![]() $\psi '=\varrho ^{-1}_\tau \circ \psi $
. Then
$\psi '=\varrho ^{-1}_\tau \circ \psi $
. Then
![]() $\psi '$
is m-lifting, because if
$\psi '$
is m-lifting, because if
![]() $\varphi $
is
$\varphi $
is
![]() $\mathrm {r}\Sigma _{m+1}$
and
$\mathrm {r}\Sigma _{m+1}$
and
![]() ${\bar {U}}\models \varphi (x)$
then easily
${\bar {U}}\models \varphi (x)$
then easily
so
![]() $U\models \text {"}U'\models \varphi (\psi '(x))\text {"}$
, so
$U\models \text {"}U'\models \varphi (\psi '(x))\text {"}$
, so
![]() $U'\models \varphi (\psi '(x))$
. Also
$U'\models \varphi (\psi '(x))$
. Also
![]() $\psi '\!\upharpoonright \!{\bar {\tau }}=\pi \!\upharpoonright \!{\bar {\tau }}$
. And
$\psi '\!\upharpoonright \!{\bar {\tau }}=\pi \!\upharpoonright \!{\bar {\tau }}$
. And
![]() $\psi '$
is c-preserving; if
$\psi '$
is c-preserving; if
![]() $m=0$
and M has largest cardinal
$m=0$
and M has largest cardinal
![]() $\Omega $
, this follows easily from commutativity and the fact that we put
$\Omega $
, this follows easily from commutativity and the fact that we put
![]() $\Omega \in \mathrm {rg}(\pi )$
, and if
$\Omega \in \mathrm {rg}(\pi )$
, and if
![]() $m=0$
and M has no largest cardinal then it is because then for any M-cardinal
$m=0$
and M has no largest cardinal then it is because then for any M-cardinal
![]() $\xi $
, we have
$\xi $
, we have
![]() $M|\xi \preccurlyeq _1 M$
by condensation, and hence,
$M|\xi \preccurlyeq _1 M$
by condensation, and hence,
![]() $\kappa <\max (q)$
(as
$\kappa <\max (q)$
(as
![]() $\kappa \in \mathrm {rg}(\pi )$
), and so
$\kappa \in \mathrm {rg}(\pi )$
), and so
![]() ${\bar {M}},M_\kappa $
have largest cardinals
${\bar {M}},M_\kappa $
have largest cardinals
![]() $\Psi _\omega ,\Psi _\kappa $
respectively, with
$\Psi _\omega ,\Psi _\kappa $
respectively, with
![]() $\pi (\Psi _\omega )=\pi _\kappa (\Psi _\kappa )=\mathrm {card}^M(\max (q))$
.
$\pi (\Psi _\omega )=\pi _\kappa (\Psi _\kappa )=\mathrm {card}^M(\max (q))$
.
For
![]() $\eta <\theta $
, let
$\eta <\theta $
, let
and
![]() $\pi _\eta :M_\eta \to M$
be the uncollapse and
$\pi _\eta :M_\eta \to M$
be the uncollapse and
![]() $\sigma _\eta :{\bar {M}}\to M_\eta $
the natural map, so
$\sigma _\eta :{\bar {M}}\to M_\eta $
the natural map, so
![]() ${\pi _\eta \circ \sigma _\eta =\pi }$
. Since
${\pi _\eta \circ \sigma _\eta =\pi }$
. Since
![]() $\eta <\theta \leq \tau \leq \rho _{m+1}^M$
, we have
$\eta <\theta \leq \tau \leq \rho _{m+1}^M$
, we have
![]() $M_\eta \in M$
. Note that if
$M_\eta \in M$
. Note that if
![]() $\eta $
is an M-cardinal then
$\eta $
is an M-cardinal then
![]() $M_\eta $
is
$M_\eta $
is
![]() $(m+1)$
-sound with
$(m+1)$
-sound with
![]() $\eta =\rho _{m+1}^{M_\eta }$
and
$\eta =\rho _{m+1}^{M_\eta }$
and
![]() $p_{m+1}^{M_\eta }=\sigma _\eta ({\bar {q}})\backslash \eta $
, so
$p_{m+1}^{M_\eta }=\sigma _\eta ({\bar {q}})\backslash \eta $
, so
![]() $M_\eta \triangleleft M|\theta $
.
$M_\eta \triangleleft M|\theta $
.
Now as before, we consider two cases.
Case 1.
![]() $\pi "{\bar {\theta }}$
is bounded in
$\pi "{\bar {\theta }}$
is bounded in
![]() $\theta $
. Let
$\theta $
. Let
![]() $\eta =\sup \pi "{\bar {\theta }}$
. We have
$\eta =\sup \pi "{\bar {\theta }}$
. We have
![]() $M_\eta $
, etc., as above. Note that either:
$M_\eta $
, etc., as above. Note that either:
-
–
 $\eta $
is a limit cardinal of M (hence the comments above apply), or
$\eta $
is a limit cardinal of M (hence the comments above apply), or -
–
 $M||\eta $
has largest cardinal
$M||\eta $
has largest cardinal
 $\xi $
where
$\xi $
where
 $\xi $
is an M-cardinal and
$\xi $
is an M-cardinal and
 $\xi \in \mathrm {rg}(\pi )$
, and because
$\xi \in \mathrm {rg}(\pi )$
, and because $$\begin{align*}\eta\subseteq\mathrm{Hull}_{m+1}^M(\xi\cup\{q\})=\mathrm{Hull}_{m+1}^M(\eta\cup\{q\}), \end{align*}$$
$$\begin{align*}\eta\subseteq\mathrm{Hull}_{m+1}^M(\xi\cup\{q\})=\mathrm{Hull}_{m+1}^M(\eta\cup\{q\}), \end{align*}$$
 $\mathrm {rg}(\pi )=\mathrm {Hull}_{m+1}^M(\{q\})$
is cofinal in
$\mathrm {rg}(\pi )=\mathrm {Hull}_{m+1}^M(\{q\})$
is cofinal in
 $\eta $
; therefore,
$\eta $
; therefore,
 $\rho _{m+1}^{M_\eta }=\xi $
and
$\rho _{m+1}^{M_\eta }=\xi $
and
 $p_{m+1}^{M_\eta }=\sigma _\eta ({\bar {q}})\backslash \xi $
.
$p_{m+1}^{M_\eta }=\sigma _\eta ({\bar {q}})\backslash \xi $
.
It follows that
![]() $M_\eta $
is sound, and
$M_\eta $
is sound, and
![]() $\mathrm {cr}(\pi _\eta )\geq \eta $
. Since
$\mathrm {cr}(\pi _\eta )\geq \eta $
. Since
![]() $\eta <\theta \leq \rho _{m+1}^M$
, condensation (see [Reference Schlutzenberg9, Theorem 5.2]) gives
$\eta <\theta \leq \rho _{m+1}^M$
, condensation (see [Reference Schlutzenberg9, Theorem 5.2]) gives
![]() $M_\eta \triangleleft M|\theta $
. Note that
$M_\eta \triangleleft M|\theta $
. Note that
![]() $\sigma _\eta \!\upharpoonright \!{\bar {\theta }}=\pi \!\upharpoonright \!{\bar {\theta }}$
and
$\sigma _\eta \!\upharpoonright \!{\bar {\theta }}=\pi \!\upharpoonright \!{\bar {\theta }}$
and
![]() $\sigma _\eta \in M|\theta $
. Since
$\sigma _\eta \in M|\theta $
. Since
![]() $M|\theta =U|\theta $
, therefore
$M|\theta =U|\theta $
, therefore
![]() $M_\eta \triangleleft U|\theta $
and
$M_\eta \triangleleft U|\theta $
and
![]() $\sigma _\eta \in U|\theta $
. Note that
$\sigma _\eta \in U|\theta $
. Note that
![]() $M_\eta \triangleleft \mathfrak {C}_0(U')$
as
$M_\eta \triangleleft \mathfrak {C}_0(U')$
as
![]() $\eta <\tau $
.
$\eta <\tau $
.
Now
![]() $\sigma _\eta \!\upharpoonright \!{\bar {\theta }}=\pi \!\upharpoonright \!{\bar {\theta }}=\psi '\!\upharpoonright \!{\bar {\theta }}$
and
$\sigma _\eta \!\upharpoonright \!{\bar {\theta }}=\pi \!\upharpoonright \!{\bar {\theta }}=\psi '\!\upharpoonright \!{\bar {\theta }}$
and
![]() $\sigma _\eta ,{\bar {U}},U'\in U$
, with
$\sigma _\eta ,{\bar {U}},U'\in U$
, with
![]() ${\bar {U}}\in \mathrm {HC}^U$
, and moreover,
${\bar {U}}\in \mathrm {HC}^U$
, and moreover,
![]() $U|(\mathrm {Ord}^{U'})^{+U}$
is wellfounded. So by absoluteness, in U there is some c-preserving m-lifting embedding
$U|(\mathrm {Ord}^{U'})^{+U}$
is wellfounded. So by absoluteness, in U there is some c-preserving m-lifting embedding
![]() $\widetilde {\psi }:{\bar {U}}\to U'$
with
$\widetilde {\psi }:{\bar {U}}\to U'$
with
![]() $\widetilde {\psi }\!\upharpoonright \!{\bar {\theta }}=\sigma _\eta \!\upharpoonright \!{\bar {\theta }}$
.
$\widetilde {\psi }\!\upharpoonright \!{\bar {\theta }}=\sigma _\eta \!\upharpoonright \!{\bar {\theta }}$
.
So
![]() $U\models \varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$
, where
$U\models \varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$
, where
![]() $\varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$
asserts “There are proper segments
$\varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$
asserts “There are proper segments
![]() $M^*$
and
$M^*$
and
![]() $U^*$
of me, with
$U^*$
of me, with
![]() $M^*\triangleleft \mathfrak {C}_0(U^*)$
, and there are c-preserving m-lifting embeddings
$M^*\triangleleft \mathfrak {C}_0(U^*)$
, and there are c-preserving m-lifting embeddings
such that
![]() $\pi ^*\!\upharpoonright \!{\bar {\theta }}=\psi ^*\!\upharpoonright \!{\bar {\theta }}$
and if
$\pi ^*\!\upharpoonright \!{\bar {\theta }}=\psi ^*\!\upharpoonright \!{\bar {\theta }}$
and if
![]() $\bar {M}|\bar {\theta }$
has largest cardinal
$\bar {M}|\bar {\theta }$
has largest cardinal
![]() $\bar {\xi }$
then
$\bar {\xi }$
then
![]() $\rho _{m+1}^{M^*}=\pi ^*(\bar {\xi })$
”.
$\rho _{m+1}^{M^*}=\pi ^*(\bar {\xi })$
”.
So by elementarity,
![]() $M\models \varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$
. Let
$M\models \varphi ^+({\bar {M}},{\bar {U}},{\bar {\theta }})$
. Let
![]() $M^*,U^*,\pi ^*,\psi ^*$
witness this in M. These embeddings are enough to copy m-maximal trees on
$M^*,U^*,\pi ^*,\psi ^*$
witness this in M. These embeddings are enough to copy m-maximal trees on
![]() $\mathfrak {P}$
to m-maximal trees on M. Let us point out one detail of the copying process. Suppose
$\mathfrak {P}$
to m-maximal trees on M. Let us point out one detail of the copying process. Suppose
![]() $\bar {M}|{\bar {\theta }}$
has largest cardinal
$\bar {M}|{\bar {\theta }}$
has largest cardinal
![]() $\bar {\xi }$
and let
$\bar {\xi }$
and let
![]() $\xi ^*=\pi ^*(\bar {\xi })$
. Then
$\xi ^*=\pi ^*(\bar {\xi })$
. Then
![]() $\rho _{m+1}^{M^*}=\xi ^*$
and
$\rho _{m+1}^{M^*}=\xi ^*$
and
When iterating
![]() $\mathfrak {P}$
, extenders G with
$\mathfrak {P}$
, extenders G with
![]() $\mathrm {cr}(G)=\bar {\xi }$
apply to
$\mathrm {cr}(G)=\bar {\xi }$
apply to
![]() ${\bar {M}}$
. Let
${\bar {M}}$
. Let
![]() $G^*$
be the lift of G. Then
$G^*$
be the lift of G. Then
![]() $\mathrm {cr}(G^*)=\xi ^*$
and
$\mathrm {cr}(G^*)=\xi ^*$
and
![]() $G^*$
is
$G^*$
is
![]() $U^*$
-total. From line (5), it follows that we can define a copy map
$U^*$
-total. From line (5), it follows that we can define a copy map
in the usual manner. Otherwise the copying is routine.Footnote 15
Case 2.
![]() $\pi "{\bar {\theta }}$
is unbounded in
$\pi "{\bar {\theta }}$
is unbounded in
![]() $\theta $
.
$\theta $
.
Then
![]() $\theta $
is a limit cardinal of M, because
$\theta $
is a limit cardinal of M, because
![]() $\theta $
is an M-cardinal
$\theta $
is an M-cardinal
![]() ${\leq \rho _{m+1}^M}$
and there is an
${\leq \rho _{m+1}^M}$
and there is an ![]() -definable cofinal partial map
-definable cofinal partial map
![]() $\omega \to \sup \pi "{\bar {\theta }}$
. For each M-cardinal
$\omega \to \sup \pi "{\bar {\theta }}$
. For each M-cardinal
![]() $\mu <\theta $
we have
$\mu <\theta $
we have
![]() $M_\mu ,\sigma _\mu \in M|\theta =U|\theta $
. We have
$M_\mu ,\sigma _\mu \in M|\theta =U|\theta $
. We have
![]() $M_\mu ,\sigma _\mu ,U'\in U|\tau ^{+U}$
.
$M_\mu ,\sigma _\mu ,U'\in U|\tau ^{+U}$
.
Let C be the set of
![]() ${\bar {M}}$
-cardinals
${\bar {M}}$
-cardinals
![]() ${<{\bar {\theta }}}$
. Working in U, let T be the tree searching for
${<{\bar {\theta }}}$
. Working in U, let T be the tree searching for
![]() $\widetilde {\psi },\widetilde {U}$
and a sequence
$\widetilde {\psi },\widetilde {U}$
and a sequence
![]() $\left <\widetilde {M}_{{\bar {\mu }}},\widetilde {\sigma }_{{\bar {\mu }}}\right>_{{\bar {\mu }}\in C}$
such that:
$\left <\widetilde {M}_{{\bar {\mu }}},\widetilde {\sigma }_{{\bar {\mu }}}\right>_{{\bar {\mu }}\in C}$
such that:
-
–
 $\widetilde {U}\triangleleft U|j(\kappa )^{+U},$
$\widetilde {U}\triangleleft U|j(\kappa )^{+U},$
-
–
 $\widetilde {\psi }:{\bar {U}}\to \widetilde {U}$
is c-preserving m-lifting,
$\widetilde {\psi }:{\bar {U}}\to \widetilde {U}$
is c-preserving m-lifting, -
– for each
 ${\bar {\mu }}\in C$
:
${\bar {\mu }}\in C$
:-
–
 $\widetilde {U}|\widetilde {\psi }({\bar {\mu }})\trianglelefteq \widetilde {M}_{\bar {\mu }}\triangleleft \widetilde {U}$
,
$\widetilde {U}|\widetilde {\psi }({\bar {\mu }})\trianglelefteq \widetilde {M}_{\bar {\mu }}\triangleleft \widetilde {U}$
, -
–
 $\widetilde {\sigma }_{\bar {\mu }}:{\bar {M}}\to \widetilde {M}_{\bar {\mu }}$
is c-preserving m-lifting,
$\widetilde {\sigma }_{\bar {\mu }}:{\bar {M}}\to \widetilde {M}_{\bar {\mu }}$
is c-preserving m-lifting, -
–
 $\widetilde {\sigma }_{\bar {\mu }}\!\upharpoonright \!({\bar {\mu }}+1)\subseteq \widetilde {\psi }$
.
$\widetilde {\sigma }_{\bar {\mu }}\!\upharpoonright \!({\bar {\mu }}+1)\subseteq \widetilde {\psi }$
.
-
We have that
![]() $U\models $
“T is illfounded”, because
$U\models $
“T is illfounded”, because
![]() $\psi ',U',\left <M_\mu ,\sigma _\mu \right>_\mu $
exist and
$\psi ',U',\left <M_\mu ,\sigma _\mu \right>_\mu $
exist and
![]() $U|\tau ^{+U}$
is wellfounded and models
$U|\tau ^{+U}$
is wellfounded and models
![]() $\mathrm {ZFC}^-$
.
$\mathrm {ZFC}^-$
.
Now
![]() $T=j(T^M)$
for some
$T=j(T^M)$
for some
![]() $T^M\in M$
, so
$T^M\in M$
, so
![]() $M\models $
“
$M\models $
“
![]() $T^M$
is illfounded”. But then letting
$T^M$
is illfounded”. But then letting
![]() $\widetilde {U},\widetilde {\psi },\left <\widetilde {M}_{\bar {\mu }},\widetilde {\sigma }_{\bar {\mu }}\right>_{{\bar {\mu }}\in C}$
witness this, these objects allow us to lift m-maximal trees on
$\widetilde {U},\widetilde {\psi },\left <\widetilde {M}_{\bar {\mu }},\widetilde {\sigma }_{\bar {\mu }}\right>_{{\bar {\mu }}\in C}$
witness this, these objects allow us to lift m-maximal trees on
![]() $\mathfrak {P}$
to m-maximal trees on M. (Here when we use an extender G with
$\mathfrak {P}$
to m-maximal trees on M. (Here when we use an extender G with
![]() $\mathrm {cr}(G)={\bar {\gamma }}<{\bar {\theta }}$
, we apply it to
$\mathrm {cr}(G)={\bar {\gamma }}<{\bar {\theta }}$
, we apply it to
![]() ${\bar {M}}$
, and our next lifting map is of the form
${\bar {M}}$
, and our next lifting map is of the form
where
![]() ${\bar {\mu }}={\bar {\gamma }}^{+\bar {M}}$
and where i is the upper ultrapower map, and
${\bar {\mu }}={\bar {\gamma }}^{+\bar {M}}$
and where i is the upper ultrapower map, and
![]() $\varphi $
is defined as usual using
$\varphi $
is defined as usual using
![]() $\widetilde {\sigma }_{{\bar {\mu }}}$
.)
$\widetilde {\sigma }_{{\bar {\mu }}}$
.)
This completes both cases, and hence, the proof that
![]() $\mathfrak {P}$
is iterable.
$\mathfrak {P}$
is iterable.
![]() $\Box $
(Claim 1)
$\Box $
(Claim 1)
We have
![]() ${\bar {M}}|{\bar {\theta }}={\bar {U}}|{\bar {\theta }}$
. So comparison of
${\bar {M}}|{\bar {\theta }}={\bar {U}}|{\bar {\theta }}$
. So comparison of
![]() $(\mathfrak {P},{\bar {M}})$
uses only extenders indexed above
$(\mathfrak {P},{\bar {M}})$
uses only extenders indexed above
![]() ${\bar {\theta }}$
. So by the claim, there is a successful such comparison
${\bar {\theta }}$
. So by the claim, there is a successful such comparison
![]() $(\mathcal {U},\mathcal {T})$
.
$(\mathcal {U},\mathcal {T})$
.
Claim 2. We have
![]() $:$
$:$
-
1.
 $M^{\mathcal {U}}_\infty =M^{\mathcal {T}}_\infty $
,
$M^{\mathcal {U}}_\infty =M^{\mathcal {T}}_\infty $
,
 $b^{\mathcal {U}},b^{\mathcal {T}}$
do not drop in model or degree,
$b^{\mathcal {U}},b^{\mathcal {T}}$
do not drop in model or degree,
 $b^{\mathcal {U}}$
is above
$b^{\mathcal {U}}$
is above
 ${\bar {U}}$
and
${\bar {U}}$
and
 ${i^{\mathcal {U}}\circ {\bar {j}}=i^{\mathcal {T}}}$
.
${i^{\mathcal {U}}\circ {\bar {j}}=i^{\mathcal {T}}}$
. -
2.
 ${\bar {\theta }}={\bar {\tau }}$
, so
${\bar {\theta }}={\bar {\tau }}$
, so
 $\theta =\tau $
.
$\theta =\tau $
. -
3.
 ${\bar {U}}|{\bar {\tau }}^{+{\bar {U}}}={\bar {M}}||{\bar {\tau }}^{+{\bar {U}}}$
, so
${\bar {U}}|{\bar {\tau }}^{+{\bar {U}}}={\bar {M}}||{\bar {\tau }}^{+{\bar {U}}}$
, so
 $U|\tau ^{+U}=M||\tau ^{+M}$
.
$U|\tau ^{+U}=M||\tau ^{+M}$
. -
4. If E is explicitly Dodd-solid above
 $\tau $
then
$\tau $
then
 ${\bar {E}}\in \mathbb {E}_+^{{\bar {M}}}$
, so
${\bar {E}}\in \mathbb {E}_+^{{\bar {M}}}$
, so
 $E\in \mathbb {E}_+^M$
.
$E\in \mathbb {E}_+^M$
.
Proof Because
![]() ${\bar {M}}$
is
${\bar {M}}$
is
![]() $(m+1)$
-sound and
$(m+1)$
-sound and
![]() $\rho _{m+1}^{\bar {M}}=\omega $
, standard arguments give part 1.
$\rho _{m+1}^{\bar {M}}=\omega $
, standard arguments give part 1.
Part 2: Suppose that
![]() ${\bar {\theta }}<{\bar {\tau }}$
. Then since
${\bar {\theta }}<{\bar {\tau }}$
. Then since
![]() $\mathcal {H}_{\bar {\tau }}^{\bar {M}}\subseteq {\bar {U}}$
, we have
$\mathcal {H}_{\bar {\tau }}^{\bar {M}}\subseteq {\bar {U}}$
, we have
![]() ${\bar {\theta }}^{+{\bar {U}}}={\bar {\theta }}^{+{\bar {M}}}$
. But then since
${\bar {\theta }}^{+{\bar {U}}}={\bar {\theta }}^{+{\bar {M}}}$
. But then since
![]() $b^{\mathcal {U}}$
is above
$b^{\mathcal {U}}$
is above
![]() ${\bar {U}}$
and does not drop,
${\bar {U}}$
and does not drop,
contradicting the choice of
![]() $\theta $
(and hence
$\theta $
(and hence
![]() ${\bar {\theta }}$
).
${\bar {\theta }}$
).
Part 3: Much as in part 2, but now with
![]() ${\bar {\tau }}={\bar {\theta }}$
, so
${\bar {\tau }}={\bar {\theta }}$
, so
![]() $\mathrm {cr}(i^{\mathcal {U}})\geq {\bar {\tau }}$
. The conclusion that
$\mathrm {cr}(i^{\mathcal {U}})\geq {\bar {\tau }}$
. The conclusion that
![]() $U|\tau ^{+U}=M||\tau ^{+U}$
follows from the reflection between
$U|\tau ^{+U}=M||\tau ^{+U}$
follows from the reflection between
![]() ${\bar {M}}$
and M discussed earlier.
${\bar {M}}$
and M discussed earlier.
Part 4: If
![]() ${\bar {E}}\in \mathbb {E}^{\bar {M}}$
, note that
${\bar {E}}\in \mathbb {E}^{\bar {M}}$
, note that
![]() ${\bar {E}}\in \mathbb {E}(\mathfrak {C}_0({\bar {M}}))$
, since
${\bar {E}}\in \mathbb {E}(\mathfrak {C}_0({\bar {M}}))$
, since
![]() ${\bar {\tau }}<\rho _0^{\bar {M}}$
; it easily follows then that
${\bar {\tau }}<\rho _0^{\bar {M}}$
; it easily follows then that
![]() $E=\pi ({\bar {E}})$
, just by the elementarity of
$E=\pi ({\bar {E}})$
, just by the elementarity of
![]() $\pi $
. Similarly if
$\pi $
. Similarly if
![]() ${\bar {E}}=F^{\bar {M}}$
then
${\bar {E}}=F^{\bar {M}}$
then
![]() $E=F^M$
by elementarity. So we just need to see that
$E=F^M$
by elementarity. So we just need to see that
![]() ${\bar {E}}\in \mathbb {E}_+^{\bar {M}}$
, assuming that E is explicitly Dodd-solid above
${\bar {E}}\in \mathbb {E}_+^{\bar {M}}$
, assuming that E is explicitly Dodd-solid above
![]() $\tau $
.
$\tau $
.
If
![]() $t=\emptyset $
then this follows from the ISC as in the proof of the ISC for pseudo-mice. Suppose instead that E is explicitly Dodd-solid above
$t=\emptyset $
then this follows from the ISC as in the proof of the ISC for pseudo-mice. Suppose instead that E is explicitly Dodd-solid above
![]() $\tau $
and
$\tau $
and
![]() $t\neq \emptyset $
. So as discussed earlier,
$t\neq \emptyset $
. So as discussed earlier,
![]() ${\bar {E}}$
is Dodd-solid with respect to
${\bar {E}}$
is Dodd-solid with respect to
![]() ${\bar {t}}$
. Since
${\bar {t}}$
. Since
![]() ${\bar {M}}$
is
${\bar {M}}$
is
![]() $1$
-sound and iterable, by 2.14 and as in [Reference Schlutzenberg11, Section 2], we can analyse the Dodd-structure of the extenders used in
$1$
-sound and iterable, by 2.14 and as in [Reference Schlutzenberg11, Section 2], we can analyse the Dodd-structure of the extenders used in
![]() $\mathcal {T}$
, decomposing them into Dodd-sound extenders. As there, there is exactly one extender
$\mathcal {T}$
, decomposing them into Dodd-sound extenders. As there, there is exactly one extender
![]() $G=E^{\mathcal {T}}_\alpha $
used along
$G=E^{\mathcal {T}}_\alpha $
used along
![]() $b^{\mathcal {T}}$
, G has largest generator
$b^{\mathcal {T}}$
, G has largest generator
![]() $\gamma =i^{\mathcal {U}}(\max ({\bar {t}}))$
, and there is a unique
$\gamma =i^{\mathcal {U}}(\max ({\bar {t}}))$
, and there is a unique
![]() $\beta \leq _{\mathcal {T}}\alpha $
such that the Dodd-core D of G is in
$\beta \leq _{\mathcal {T}}\alpha $
such that the Dodd-core D of G is in
![]() $\mathbb {E}_+(M^{\mathcal {T}}_\beta )$
. Moreover,
$\mathbb {E}_+(M^{\mathcal {T}}_\beta )$
. Moreover,
![]() $\tau _D\leq {\bar {\tau }}$
, and if
$\tau _D\leq {\bar {\tau }}$
, and if
![]() $\beta <_{\mathcal {T}}\alpha $
, then letting
$\beta <_{\mathcal {T}}\alpha $
, then letting
![]() $\varepsilon +1=\mathrm {succ}^{\mathcal {T}}(\beta ,\alpha )$
, we have
$\varepsilon +1=\mathrm {succ}^{\mathcal {T}}(\beta ,\alpha )$
, we have
![]() $M^{*\mathcal {T}}_{\varepsilon +1}=M^{\mathcal {T}}_\beta |\mathrm {lh}(D)$
and
$M^{*\mathcal {T}}_{\varepsilon +1}=M^{\mathcal {T}}_\beta |\mathrm {lh}(D)$
and
![]() $\deg ^{\mathcal {T}}_{\varepsilon +1}=0$
, and letting
$\deg ^{\mathcal {T}}_{\varepsilon +1}=0$
, and letting
![]() $k=i^{*\mathcal {T}}_{\varepsilon +1,\alpha }$
, then
$k=i^{*\mathcal {T}}_{\varepsilon +1,\alpha }$
, then
![]() $\mathrm {cr}(k)\geq \tau _D$
,
$\mathrm {cr}(k)\geq \tau _D$
,
and
Note that
![]() $\rho _1(M^{\mathcal {T}}_\beta |\mathrm {lh}(D))\leq \tau _D\leq {\bar {\tau }}$
.
$\rho _1(M^{\mathcal {T}}_\beta |\mathrm {lh}(D))\leq \tau _D\leq {\bar {\tau }}$
.
Suppose
![]() $D\neq F^{M^{\mathcal {T}}_\beta }$
. Then
$D\neq F^{M^{\mathcal {T}}_\beta }$
. Then
![]() $\beta =0$
, as otherwise
$\beta =0$
, as otherwise
![]() ${\bar {\tau }}<\mathrm {lh}(E^{\mathcal {T}}_0)\leq \rho _1(M^{\mathcal {T}}_\beta |\mathrm {lh}(D))$
, contradiction. So
${\bar {\tau }}<\mathrm {lh}(E^{\mathcal {T}}_0)\leq \rho _1(M^{\mathcal {T}}_\beta |\mathrm {lh}(D))$
, contradiction. So
![]() $D\in \mathbb {E}^{{\bar {M}}}$
. Since
$D\in \mathbb {E}^{{\bar {M}}}$
. Since
![]() ${\bar {\tau }}$
is an
${\bar {\tau }}$
is an
![]() ${\bar {M}}$
-cardinal, therefore
${\bar {M}}$
-cardinal, therefore
![]() $\tau _D={\bar {\tau }}$
, so
$\tau _D={\bar {\tau }}$
, so
so
![]() $\bar {E}=D\in \mathbb {E}^{{\bar {M}}}$
, as desired.
$\bar {E}=D\in \mathbb {E}^{{\bar {M}}}$
, as desired.
Now suppose instead that
![]() $D=F^{M^{\mathcal {T}}_\beta }$
. Then again
$D=F^{M^{\mathcal {T}}_\beta }$
. Then again
![]() $\beta =0$
, since otherwise
$\beta =0$
, since otherwise
![]() ${\bar {\tau }}\leq \lambda (E^{\mathcal {T}}_0)<\tau _D$
, contradiction. So
${\bar {\tau }}\leq \lambda (E^{\mathcal {T}}_0)<\tau _D$
, contradiction. So
![]() $D=F^{\bar {M}}$
. We claim that
$D=F^{\bar {M}}$
. We claim that
![]() $\alpha =0$
, so
$\alpha =0$
, so
![]() $G=D$
is Dodd-sound, and it follows then (as in [Reference Schlutzenberg11]) that
$G=D$
is Dodd-sound, and it follows then (as in [Reference Schlutzenberg11]) that
![]() $\mathcal {U}$
is trivial and we are done. So suppose
$\mathcal {U}$
is trivial and we are done. So suppose
![]() $0<_{\mathcal {T}}\alpha $
; so
$0<_{\mathcal {T}}\alpha $
; so
![]() $(0,\alpha ]_{\mathcal {T}}$
does not drop in model. Let
$(0,\alpha ]_{\mathcal {T}}$
does not drop in model. Let
![]() $F^*$
be the first extender used along
$F^*$
be the first extender used along
![]() $(0,\alpha ]_{\mathcal {T}}$
. So
$(0,\alpha ]_{\mathcal {T}}$
. So
![]() ${\bar {\tau }}\leq \nu _{F^*}$
, as
${\bar {\tau }}\leq \nu _{F^*}$
, as
![]() ${\bar {\tau }}<\mathrm {lh}(E^{\mathcal {T}}_0)$
and
${\bar {\tau }}<\mathrm {lh}(E^{\mathcal {T}}_0)$
and
![]() ${\bar {\tau }}$
is an
${\bar {\tau }}$
is an
![]() ${\bar {M}}$
-cardinal. Note
${\bar {M}}$
-cardinal. Note
where
![]() $G'=F^{\mathrm {Ult}_0({\bar {M}},F^*\!\upharpoonright \!{\bar {\tau }})}$
. Therefore
$G'=F^{\mathrm {Ult}_0({\bar {M}},F^*\!\upharpoonright \!{\bar {\tau }})}$
. Therefore
![]() ${\bar {U}}$
is the iterate of
${\bar {U}}$
is the iterate of
![]() ${\bar {M}}$
given by the tree
${\bar {M}}$
given by the tree
![]() $\mathcal {T}'$
which uses exactly two extenders,
$\mathcal {T}'$
which uses exactly two extenders,
![]() $E^{\mathcal {T}'}_0=F^*\!\upharpoonright \!{\bar {\tau }}$
and
$E^{\mathcal {T}'}_0=F^*\!\upharpoonright \!{\bar {\tau }}$
and
![]() $E^{\mathcal {T}'}_1=G'$
. It follows that
$E^{\mathcal {T}'}_1=G'$
. It follows that
![]() $\mathcal {T}=\mathcal {T}'$
,
$\mathcal {T}=\mathcal {T}'$
,
![]() $\mathcal {U}$
is trivial,
$\mathcal {U}$
is trivial,
![]() $E^{\mathcal {T}}_0=F^*$
,
$E^{\mathcal {T}}_0=F^*$
,
![]() $\nu _{E^{\mathcal {T}}_0}={\bar {\tau }}$
,
$\nu _{E^{\mathcal {T}}_0}={\bar {\tau }}$
,
![]() $\tau _D\leq \mathrm {cr}(E^{\mathcal {T}}_0)<{\bar {\tau }}$
and
$\tau _D\leq \mathrm {cr}(E^{\mathcal {T}}_0)<{\bar {\tau }}$
and
![]() $E^{\mathcal {T}}_1=G=G'$
. So
$E^{\mathcal {T}}_1=G=G'$
. So
![]() $E^{\mathcal {T}}_0\neq F^{\bar {M}}$
(as
$E^{\mathcal {T}}_0\neq F^{\bar {M}}$
(as
![]() ${\bar {\kappa }}=\mathrm {cr}(E^{\mathcal {T}}_1)=\mathrm {cr}(D)$
and
${\bar {\kappa }}=\mathrm {cr}(E^{\mathcal {T}}_1)=\mathrm {cr}(D)$
and
![]() $D=F^{\bar {M}}$
), so
$D=F^{\bar {M}}$
), so
![]() $\mathrm {lh}(E^{\mathcal {T}}_0)={\bar {\tau }}^{+{\bar {U}}}=\bar {\varsigma }<{\bar {\tau }}^{+{\bar {M}}}$
,
$\mathrm {lh}(E^{\mathcal {T}}_0)={\bar {\tau }}^{+{\bar {U}}}=\bar {\varsigma }<{\bar {\tau }}^{+{\bar {M}}}$
,
![]() ${\bar {M}}|\bar {\varsigma }$
is active with
${\bar {M}}|\bar {\varsigma }$
is active with
![]() $E^{\mathcal {T}}_0$
, and
$E^{\mathcal {T}}_0$
, and
![]() ${\bar {\kappa }}<\mathrm {cr}(E^{\mathcal {T}}_0)$
. It follows that
${\bar {\kappa }}<\mathrm {cr}(E^{\mathcal {T}}_0)$
. It follows that
![]() $E^{\mathcal {T}}_0={\bar {F}}$
from property 8’ above. But then by that property,
$E^{\mathcal {T}}_0={\bar {F}}$
from property 8’ above. But then by that property,
Also
![]() ${\bar {t}}=k(t_D\backslash \mathrm {cr}(E^{\mathcal {T}}_0))$
and
${\bar {t}}=k(t_D\backslash \mathrm {cr}(E^{\mathcal {T}}_0))$
and
But then
![]() $D\in {\bar {M}}$
, contradiction.
$D\in {\bar {M}}$
, contradiction.
This completes the proof of the theorem.
3 Inductive condensation stack
In this section we prove Theorem 1.1. We first give the proofs of some older results, as their methods are then used in the proof of 1.1. The first is an observation due to Jensen.
Fact 3.1 (Jensen).
Let N be a premouse of height
![]() $\kappa>\omega $
, where
$\kappa>\omega $
, where
![]() $\kappa $
is regular. Let P be a sound premouse such that
$\kappa $
is regular. Let P be a sound premouse such that
![]() $N\trianglelefteq P$
,
$N\trianglelefteq P$
,
![]() $\rho _\omega ^P=\kappa $
, and
$\rho _\omega ^P=\kappa $
, and
![]() $\omega $
-condensation holds for P. Let Q be likewise. Then
$\omega $
-condensation holds for P. Let Q be likewise. Then
![]() $P\trianglelefteq Q$
or
$P\trianglelefteq Q$
or
![]() $Q\trianglelefteq P$
.
$Q\trianglelefteq P$
.
Proof Suppose not. Taking a hull of V, it is easy to find
![]() $\bar {P},\bar {Q}$
such that
$\bar {P},\bar {Q}$
such that
![]() ${\bar {P}\ntrianglelefteq \bar {Q}\ntrianglelefteq \bar {P}}$
and fully elementary maps
${\bar {P}\ntrianglelefteq \bar {Q}\ntrianglelefteq \bar {P}}$
and fully elementary maps
![]() $\pi :\bar {P}\to P$
and
$\pi :\bar {P}\to P$
and
![]() $\sigma :\bar {Q}\to Q$
and
$\sigma :\bar {Q}\to Q$
and
![]() $\bar {\kappa }$
such that
$\bar {\kappa }$
such that
and
![]() $\pi (\bar {\kappa })=\kappa =\sigma (\bar {\kappa })$
. So by condensation, either:
$\pi (\bar {\kappa })=\kappa =\sigma (\bar {\kappa })$
. So by condensation, either:
-
(i)
 $\bar {P}\trianglelefteq N$
and
$\bar {P}\trianglelefteq N$
and
 $\bar {Q}\trianglelefteq N$
, or
$\bar {Q}\trianglelefteq N$
, or -
(ii)
 $N|\bar {\kappa }$
is active and
$N|\bar {\kappa }$
is active and
 $\bar {P}\trianglelefteq U$
and
$\bar {P}\trianglelefteq U$
and
 $\bar {Q}\trianglelefteq U$
where
$\bar {Q}\trianglelefteq U$
where
 $U=\mathrm {Ult}(N|\bar {\kappa },F^{N|\bar {\kappa }})$
.
$U=\mathrm {Ult}(N|\bar {\kappa },F^{N|\bar {\kappa }})$
.
In either case, it follows that either
![]() $\bar {P}\trianglelefteq \bar {Q}$
or
$\bar {P}\trianglelefteq \bar {Q}$
or
![]() $\bar {Q}\trianglelefteq \bar {P}$
, a contradiction.
$\bar {Q}\trianglelefteq \bar {P}$
, a contradiction.
A slight adaptation gives:
Fact 3.2. Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse with no largest proper segment. Let
$(0,\omega _1+1)$
-iterable premouse with no largest proper segment. Let
![]() $\kappa>\omega $
be a regular cardinal of M. Let
$\kappa>\omega $
be a regular cardinal of M. Let
![]() $P\in M$
be a sound premouse such that
$P\in M$
be a sound premouse such that
![]() $M|\kappa \trianglelefteq P$
,
$M|\kappa \trianglelefteq P$
,
![]() $\rho _\omega ^P=\kappa $
, and
$\rho _\omega ^P=\kappa $
, and
![]() $\omega $
-condensation holds for P. Then
$\omega $
-condensation holds for P. Then
![]() $P\triangleleft M$
.
$P\triangleleft M$
.
Proof Use the proof above with
![]() $Q\trianglelefteq M$
such that
$Q\trianglelefteq M$
such that
![]() $P\in Q$
and
$P\in Q$
and
![]() $\rho _\omega ^Q=\kappa $
.
$\rho _\omega ^Q=\kappa $
.
A slight refinement of this argument gives:
Fact 3.3. Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse. Let
$(0,\omega _1+1)$
-iterable premouse. Let
![]() $\kappa>\omega $
be a regular cardinal of M. Let
$\kappa>\omega $
be a regular cardinal of M. Let
![]() $P\in M$
be a
$P\in M$
be a
![]() $(n+1)$
-sound premouse such that
$(n+1)$
-sound premouse such that
![]() $M|\kappa \trianglelefteq P$
,
$M|\kappa \trianglelefteq P$
,
![]() $\rho _{n+1}^P=\kappa $
, and
$\rho _{n+1}^P=\kappa $
, and
![]() $(n+1)$
-condensation holds for P. Then
$(n+1)$
-condensation holds for P. Then
![]() $P\triangleleft M$
.
$P\triangleleft M$
.
The second ingredient is an argument of Woodin’s, which is used in the proof of Corollary 1.5. Steel noticed that 1.5 follows from Theorem 1.4 combined with Woodin’s argument.
Proof of Corollary 1.5
We have that M is
![]() $(0,\omega _1+1)$
-iterable,
$(0,\omega _1+1)$
-iterable,
![]() $\kappa $
is an uncountable cardinal in M and
$\kappa $
is an uncountable cardinal in M and
![]() $\kappa ^{+M}<\mathrm {Ord}^M$
. We want to see that
$\kappa ^{+M}<\mathrm {Ord}^M$
. We want to see that
![]() $M|\kappa ^{+M}$
is definable from parameters over
$M|\kappa ^{+M}$
is definable from parameters over
![]() $\mathcal {H}=(\mathcal {H}_{\kappa ^+})^M$
. There are two cases.
$\mathcal {H}=(\mathcal {H}_{\kappa ^+})^M$
. There are two cases.
Case 1.
M has no cutpoint in
![]() $[\kappa ,\kappa ^{+M})$
.
$[\kappa ,\kappa ^{+M})$
.
Then there are unboundedly many
![]() $\gamma <\kappa ^{+M}$
indexing an M-total extender. So by 1.4, given a premouse
$\gamma <\kappa ^{+M}$
indexing an M-total extender. So by 1.4, given a premouse
![]() $P\in \mathcal {H}$
such that
$P\in \mathcal {H}$
such that
![]() $M|\kappa \trianglelefteq P$
and
$M|\kappa \trianglelefteq P$
and
![]() $\rho _\omega ^P=\kappa $
, we have
$\rho _\omega ^P=\kappa $
, we have
![]() $P\triangleleft M|\kappa ^{+M}$
iff there is
$P\triangleleft M|\kappa ^{+M}$
iff there is
![]() $E\in \mathcal {H}$
such that
$E\in \mathcal {H}$
such that
![]() $P\triangleleft \mathrm {Ult}(M|\kappa ,E)$
and
$P\triangleleft \mathrm {Ult}(M|\kappa ,E)$
and
![]() $\mathcal {H}\models $
“E is a countably complete short extender”. This gives a definition of
$\mathcal {H}\models $
“E is a countably complete short extender”. This gives a definition of
![]() $M|\kappa ^{+M}$
over
$M|\kappa ^{+M}$
over
![]() $\mathcal {H}$
from the parameter
$\mathcal {H}$
from the parameter
![]() $M|\kappa $
, which suffices.
$M|\kappa $
, which suffices.
Case 2. Otherwise (M has a cutpoint
![]() $\gamma _0\in [\kappa ,\kappa ^{+M})$
).
$\gamma _0\in [\kappa ,\kappa ^{+M})$
).
The proof in this case is due to Woodin, and was found earlier. Let X be the set of all
![]() $H\in \mathrm {HC}^M$
such that there is
$H\in \mathrm {HC}^M$
such that there is
![]() $P\triangleleft M|\kappa ^{+M}$
and
$P\triangleleft M|\kappa ^{+M}$
and
![]() $\pi \in M$
such that
$\pi \in M$
such that
![]() $\pi :H\to P$
is elementary. Since
$\pi :H\to P$
is elementary. Since
![]() $\kappa ^{+M}<\mathrm {Ord}^M$
, we have
$\kappa ^{+M}<\mathrm {Ord}^M$
, we have
![]() $X\in M$
and X is essentially a subset of
$X\in M$
and X is essentially a subset of
![]() $\omega _1^M$
in M. So
$\omega _1^M$
in M. So
![]() $X\in \mathcal {H}$
. Let
$X\in \mathcal {H}$
. Let
![]() $P\in M$
be a sound premouse such that
$P\in M$
be a sound premouse such that
![]() $M|\gamma _0\trianglelefteq P$
,
$M|\gamma _0\trianglelefteq P$
,
![]() $\gamma _0$
is a cutpoint of P and
$\gamma _0$
is a cutpoint of P and
![]() $\rho _\omega ^P\leq \gamma _0$
. We claim that the following are equivalent:
$\rho _\omega ^P\leq \gamma _0$
. We claim that the following are equivalent:
-
(i)
 $P\triangleleft M$
,
$P\triangleleft M$
, -
(ii)
 $\mathcal {H}\models \text {"Every countable elementary submodel of }P\text { is in }X\text {"}$
.
$\mathcal {H}\models \text {"Every countable elementary submodel of }P\text { is in }X\text {"}$
.
It follows that
![]() $M|\kappa ^{+M}$
is definable over
$M|\kappa ^{+M}$
is definable over
![]() $\mathcal {H}$
from the parameter
$\mathcal {H}$
from the parameter
![]() $(X,M|\gamma _0)$
, which suffices. Now (i) implies (ii) by definition. So suppose (ii) holds. Let Q be such that
$(X,M|\gamma _0)$
, which suffices. Now (i) implies (ii) by definition. So suppose (ii) holds. Let Q be such that
![]() $P\in Q\triangleleft M$
, with
$P\in Q\triangleleft M$
, with
![]() $\rho _\omega ^{Q}\leq \gamma _0$
. Working in M, let
$\rho _\omega ^{Q}\leq \gamma _0$
. Working in M, let
![]() $Y\preccurlyeq Q$
be countable, with
$Y\preccurlyeq Q$
be countable, with
![]() $P\in Y$
. The transitive collapses
$P\in Y$
. The transitive collapses
![]() ${\bar {P}}$
of
${\bar {P}}$
of
![]() $Y\cap P$
and
$Y\cap P$
and
![]() ${\bar {Q}}$
of Y are in X, so can be compared in V. But
${\bar {Q}}$
of Y are in X, so can be compared in V. But
![]() ${\bar {P}}|{\bar {\gamma }}_0={\bar {Q}}|{\bar {\gamma }}_0$
where
${\bar {P}}|{\bar {\gamma }}_0={\bar {Q}}|{\bar {\gamma }}_0$
where
![]() ${\bar {\gamma }}_0$
is a cutpoint of both
${\bar {\gamma }}_0$
is a cutpoint of both
![]() ${\bar {P}},{\bar {Q}}$
, and
${\bar {P}},{\bar {Q}}$
, and
![]() ${\bar {P}},{\bar {Q}}$
are sound and project
${\bar {P}},{\bar {Q}}$
are sound and project
![]() $\leq {\bar {\gamma }}_0$
. So standard calculations give that
$\leq {\bar {\gamma }}_0$
. So standard calculations give that
![]() ${\bar {P}}\trianglelefteq {\bar {Q}}$
, so
${\bar {P}}\trianglelefteq {\bar {Q}}$
, so
![]() $P\trianglelefteq Q$
.
$P\trianglelefteq Q$
.
Woodin’s argument above makes use of the parameter X. We can actually replace this parameter with ![]() :
:
Lemma 3.4. Let N be an
![]() $(0,\omega _1+1)$
-iterable premouse with no largest proper segment. Let
$(0,\omega _1+1)$
-iterable premouse with no largest proper segment. Let
![]() $M\triangleleft N$
and
$M\triangleleft N$
and
![]() $H\in \mathrm {HC}^N$
and
$H\in \mathrm {HC}^N$
and
![]() $\pi :H\to M$
be elementary with
$\pi :H\to M$
be elementary with
![]() $\pi \in N$
. Then there is
$\pi \in N$
. Then there is
![]() ${\bar {M}}\triangleleft N|\omega _1^N$
and an elementary
${\bar {M}}\triangleleft N|\omega _1^N$
and an elementary
![]() $\bar {\pi }:H\to {\bar {M}}$
with
$\bar {\pi }:H\to {\bar {M}}$
with
![]() $\bar {\pi }\in N$
.
$\bar {\pi }\in N$
.
Proof Let
![]() $M\triangleleft P\triangleleft N$
be such that
$M\triangleleft P\triangleleft N$
be such that
![]() $\pi \in P$
. Let
$\pi \in P$
. Let
![]() $q\in [\mathrm {Ord}^P]^{<\omega }$
be such that
$q\in [\mathrm {Ord}^P]^{<\omega }$
be such that
![]() $(\omega ,q)$
is
$(\omega ,q)$
is
![]() $1$
-self-solid for P and such that
$1$
-self-solid for P and such that
![]() $\pi ,H,M\in \mathrm {Hull}_1^P(\{q\})$
. Let
$\pi ,H,M\in \mathrm {Hull}_1^P(\{q\})$
. Let
![]() ${\bar {P}}=\mathrm {cHull}_1^P(\{q\})$
. Then by 2.3,
${\bar {P}}=\mathrm {cHull}_1^P(\{q\})$
. Then by 2.3,
![]() ${\bar {P}}\triangleleft N|\omega _1^N$
. Let
${\bar {P}}\triangleleft N|\omega _1^N$
. Let
![]() $\sigma :{\bar {P}}\to P$
be the uncollapse. Then
$\sigma :{\bar {P}}\to P$
be the uncollapse. Then
![]() $\sigma (H)=H$
. Let
$\sigma (H)=H$
. Let
![]() $\sigma (\bar {\pi })=\pi $
and
$\sigma (\bar {\pi })=\pi $
and
![]() $\sigma ({\bar {M}})=M$
. Then
$\sigma ({\bar {M}})=M$
. Then
![]() ${\bar {M}}\triangleleft {\bar {P}}$
and
${\bar {M}}\triangleleft {\bar {P}}$
and
![]() $\bar {\pi }:H\to {\bar {M}}$
elementarily, so we are done.
$\bar {\pi }:H\to {\bar {M}}$
elementarily, so we are done.
Similarly:
Lemma 3.5. Let N be a
![]() $(0,\omega _1+1)$
-iterable premouse. Let
$(0,\omega _1+1)$
-iterable premouse. Let
![]() $M\triangleleft N$
and
$M\triangleleft N$
and
![]() $H\in \mathrm {HC}^N$
and
$H\in \mathrm {HC}^N$
and
![]() $m<\omega $
and
$m<\omega $
and
![]() $\pi :H\to M$
be an m-lifting ((weak, near) m-embedding respectively) with
$\pi :H\to M$
be an m-lifting ((weak, near) m-embedding respectively) with
![]() $\pi \in N$
. Then there is
$\pi \in N$
. Then there is
![]() ${\bar {M}}\triangleleft N|\omega _1^N$
and an m-lifting ((weak, near) m-embedding respectively)
${\bar {M}}\triangleleft N|\omega _1^N$
and an m-lifting ((weak, near) m-embedding respectively)
![]() $\bar {\pi }:H\to {\bar {M}}$
with
$\bar {\pi }:H\to {\bar {M}}$
with
![]() $\bar {\pi }\in N$
.
$\bar {\pi }\in N$
.
Proof Consider the case that
![]() $N=\mathcal {J}(M)$
and
$N=\mathcal {J}(M)$
and
![]() $\pi :H\to M$
. Then there is
$\pi :H\to M$
. Then there is
![]() $k<\omega $
and
$k<\omega $
and
![]() $x\in M$
such that
$x\in M$
such that
![]() $\pi $
is
$\pi $
is
![]() $\mathrm {r}\Sigma _k^M(\{x\})$
. Argue as in the proof of 3.4, but at degree n instead of
$\mathrm {r}\Sigma _k^M(\{x\})$
. Argue as in the proof of 3.4, but at degree n instead of
![]() $1$
, with
$1$
, with
![]() $n>k+m+5$
.
$n>k+m+5$
.
Woodin’s argument above is abstracted into the following definition:
Definition 3.6. Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse satisfying “
$(0,\omega _1+1)$
-iterable premouse satisfying “
![]() $\omega _1$
exists”, with no largest proper segment. Then
$\omega _1$
exists”, with no largest proper segment. Then
![]() $\mathrm {css}^M$
(countable substructures) denotes the set of all
$\mathrm {css}^M$
(countable substructures) denotes the set of all
![]() $H\in \mathrm {HC}^M$
such that for some
$H\in \mathrm {HC}^M$
such that for some
![]() $Q\triangleleft M$
, there is
$Q\triangleleft M$
, there is
![]() $\pi \in M$
such that
$\pi \in M$
such that
![]() $\pi :H\to Q$
is elementary. (So by 3.4,
$\pi :H\to Q$
is elementary. (So by 3.4,
![]() $\mathrm {css}^M$
is definable over
$\mathrm {css}^M$
is definable over ![]() , uniformly in M.) Let
, uniformly in M.) Let
![]() $P,Q\in M$
be sound premice. Working in M, say that Q is
$P,Q\in M$
be sound premice. Working in M, say that Q is ![]() -verified iff the transitive collapse of every countable elementary substructure of Q is in
-verified iff the transitive collapse of every countable elementary substructure of Q is in
![]() $\mathrm {css}^M$
, and say that Q is an
$\mathrm {css}^M$
, and say that Q is an ![]() -lower part premouse iff
-lower part premouse iff
![]() $P\trianglelefteq Q$
, P is a cutpoint of Q,
$P\trianglelefteq Q$
, P is a cutpoint of Q,
![]() $\rho _\omega ^Q\leq \mathrm {Ord}^P$
and Q is
$\rho _\omega ^Q\leq \mathrm {Ord}^P$
and Q is ![]() -verified. The stack of all
-verified. The stack of all ![]() -lower part premice
-lower part premice
![]() $Q\in M$
is denoted
$Q\in M$
is denoted ![]() .
.
Note that ![]() is definable over
is definable over
![]() $\left \lfloor M\right \rfloor $
from
$\left \lfloor M\right \rfloor $
from ![]() ; the fact that it forms a stack follows from the proof of 1.5.
; the fact that it forms a stack follows from the proof of 1.5.
In order to prove Theorem 1.1, it easily suffices to prove that if M is passive,
![]() $(0,\omega _1+1)$
-iterable and satisfies
$(0,\omega _1+1)$
-iterable and satisfies
![]() $\mathrm {ZFC}^-+$
“
$\mathrm {ZFC}^-+$
“
![]() $\omega _1$
exists”, then
$\omega _1$
exists”, then
![]() $\mathbb {E}^M$
is definable over
$\mathbb {E}^M$
is definable over
![]() $\left \lfloor M\right \rfloor $
from
$\left \lfloor M\right \rfloor $
from
![]() $\mathbb {E}^M\!\upharpoonright \!\omega _1^M$
, uniformly in M. We will in fact prove a stronger fact, Theorem 3.11, making do with less than
$\mathbb {E}^M\!\upharpoonright \!\omega _1^M$
, uniformly in M. We will in fact prove a stronger fact, Theorem 3.11, making do with less than
![]() $\mathrm {ZFC}^-$
. We may assume that M has a largest cardinal
$\mathrm {ZFC}^-$
. We may assume that M has a largest cardinal
![]() $\theta $
. The proof breaks into different cases, depending on the nature of M above
$\theta $
. The proof breaks into different cases, depending on the nature of M above
![]() $\theta $
. Clearly the cases are not mutually exclusive (case (i) is in fact subsumed by case (iv)).
$\theta $
. Clearly the cases are not mutually exclusive (case (i) is in fact subsumed by case (iv)).
Definition 3.7. Let M be a premouse. Let
![]() $\kappa <\theta $
be cardinals of M. We say that
$\kappa <\theta $
be cardinals of M. We say that
![]() $\kappa $
is
$\kappa $
is
![]() $\mathcal {H}_\theta $
-strong in M iff there is
$\mathcal {H}_\theta $
-strong in M iff there is
![]() $E\in M$
such that
$E\in M$
such that
![]() $M\models $
“E is a countably complete short extender” and
$M\models $
“E is a countably complete short extender” and
![]() $\mathrm {cr}(E)=\kappa $
and
$\mathrm {cr}(E)=\kappa $
and
![]() $\mathcal {H}^M_\theta \subseteq \mathrm {Ult}_0(M,E)$
.
$\mathcal {H}^M_\theta \subseteq \mathrm {Ult}_0(M,E)$
.
Definition 3.8. A passive premouse M is eventually constructible iff
![]() $M=\mathcal {J}_\alpha (R)$
for some
$M=\mathcal {J}_\alpha (R)$
for some
![]() $R\triangleleft M$
and
$R\triangleleft M$
and
![]() $\alpha>0$
.
$\alpha>0$
.
Remark 3.9. In the theorem statement below, in each case we specify definability classes
![]() $\Gamma ,\Lambda $
. The case specification is
$\Gamma ,\Lambda $
. The case specification is
![]() $\Gamma ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
, meaning that there is a
$\Gamma ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
, meaning that there is a
![]() $\Gamma $
formula
$\Gamma $
formula
![]() $\varphi $
such that for any
$\varphi $
such that for any
![]() $(0,\omega _1+1)$
-iterable premouse M satisfying “
$(0,\omega _1+1)$
-iterable premouse M satisfying “
![]() $\omega _1$
exists and
$\omega _1$
exists and
![]() $\theta $
is the largest cardinal”, the case hypothesis holds of M iff
$\theta $
is the largest cardinal”, the case hypothesis holds of M iff
![]() $\left \lfloor M\right \rfloor \models \varphi (M|\theta )$
. In the given case, the definition of
$\left \lfloor M\right \rfloor \models \varphi (M|\theta )$
. In the given case, the definition of
![]() $\mathbb {E}^M$
is
$\mathbb {E}^M$
is
![]() $\Lambda ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
. (The definability of the case specification is used in defining
$\Lambda ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
. (The definability of the case specification is used in defining
![]() $M|\theta $
from
$M|\theta $
from ![]() over
over
![]() $\left \lfloor M\right \rfloor $
.)
$\left \lfloor M\right \rfloor $
.)
Definition 3.10. Let M be a passive premouse with a largest cardinal
![]() $\theta \geq \omega _1^M$
. We say that M is tractable iff either:
$\theta \geq \omega _1^M$
. We say that M is tractable iff either:
-
(i)
 $\theta $
is regular in M, or
$\theta $
is regular in M, or -
(ii)
 $\theta $
is a cutpoint of M, or
$\theta $
is a cutpoint of M, or -
(iii) M has no cutpoint in
 $[\theta ,\mathrm {Ord}^M)$
, or
$[\theta ,\mathrm {Ord}^M)$
, or -
(iv)
 $\mathrm {cof}^M(\theta )>\omega $
, or
$\mathrm {cof}^M(\theta )>\omega $
, or -
(v)
 $M\models $
“
$M\models $
“
 $\theta $
is not a limit of cardinals which are
$\theta $
is not a limit of cardinals which are
 $\mathcal {H}_\theta $
-strong”, or
$\mathcal {H}_\theta $
-strong”, or -
(vi)
 , or
, or -
(vii)
 and M is eventually constructible.
and M is eventually constructible.
Theorem 3.11. Let M be a passive
![]() $(0,\omega _1+1)$
-iterable premouse satisfying “
$(0,\omega _1+1)$
-iterable premouse satisfying “
![]() $\omega _1$
exists”. Then
$\omega _1$
exists”. Then
![]() $:$
$:$
-
(a) If M is tractable then
 $\mathbb {E}^M$
is
$\mathbb {E}^M$
is  , uniformly in such M.
, uniformly in such M. -
(b) If
 $\left \lfloor M\right \rfloor \models \mathrm {PS}$
then
$\left \lfloor M\right \rfloor \models \mathrm {PS}$
then
 $\mathbb {E}^M$
is
$\mathbb {E}^M$
is  , uniformly in such M.
, uniformly in such M. -
(c) Suppose that M has largest cardinal
 $\theta $
and either
$\theta $
and either
 $:$
$:$
-
(i)
 $\theta $
is regular in
$\theta $
is regular in
 $M;$
and let
$M;$
and let
 $(\Gamma ,\Lambda )=(\Pi _1,\Sigma _1)$
, or
$(\Gamma ,\Lambda )=(\Pi _1,\Sigma _1)$
, or -
(ii)
 $\theta $
is a cutpoint of
$\theta $
is a cutpoint of
 $M;$
let
$M;$
let
 $(\Gamma ,\Lambda )=(\Pi _2,\Sigma _2)$
, or
$(\Gamma ,\Lambda )=(\Pi _2,\Sigma _2)$
, or -
(iii) M has no cutpoint in
 $[\theta ,\mathrm {Ord}^M);$
let
$[\theta ,\mathrm {Ord}^M);$
let
 $(\Gamma ,\Lambda )=(\Pi _3,\Sigma _2)$
, or
$(\Gamma ,\Lambda )=(\Pi _3,\Sigma _2)$
, or -
(iv)
 $\mathrm {cof}^M(\theta )>\omega ;$
let
$\mathrm {cof}^M(\theta )>\omega ;$
let
 $(\Gamma ,\Lambda )=(\Pi _1,\Sigma _1)$
, or
$(\Gamma ,\Lambda )=(\Pi _1,\Sigma _1)$
, or -
(v)
 $M\models $
“
$M\models $
“
 $\theta $
is not a limit of
$\theta $
is not a limit of
 $\mathcal {H}_\theta $
-strong cardinals”
$\mathcal {H}_\theta $
-strong cardinals”
 $;$
let
$;$
let
 $(\Gamma ,\Lambda )=(\Sigma _3,\Sigma _1)$
, or
$(\Gamma ,\Lambda )=(\Sigma _3,\Sigma _1)$
, or -
(vi)
 Footnote
16
let
Footnote
16
let
 $(\Gamma ,\Lambda )=(\Pi _5,\Sigma _4)$
, or
$(\Gamma ,\Lambda )=(\Pi _5,\Sigma _4)$
, or -
(vii)
 and M is eventually constructible; let
and M is eventually constructible; let
 $(\Gamma ,\Lambda )=(\Pi _3\wedge \Sigma _3,\Sigma _3)$
.
$(\Gamma ,\Lambda )=(\Pi _3\wedge \Sigma _3,\Sigma _3)$
.
Then
 $\mathbb {E}^M$
is
$\mathbb {E}^M$
is
 $\Lambda ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
, and the case specification is
$\Lambda ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
, and the case specification is
 $\Gamma ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
, both uniformly in such M.
$\Gamma ^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
, both uniformly in such M. -
Proof of Theorem 3.11
Parts (a) and (b) follow immediately from part (c) by an easy induction on M-cardinals.
Part (c): We split into cases corresponding to hypotheses (i)–(vii). In each case we will give a characterization of
![]() $\mathbb {E}^M$
and leave to the reader the verification of the precise degree of definability. Note that for the definability of the case specification, we use 1.2 to determine, for example, whether or not
$\mathbb {E}^M$
and leave to the reader the verification of the precise degree of definability. Note that for the definability of the case specification, we use 1.2 to determine, for example, whether or not
![]() $\theta $
is a cutpoint of M.
$\theta $
is a cutpoint of M.
Case 1.
![]() $\theta $
is regular in M.
$\theta $
is regular in M.
By 3.3, working in M, given any premouse P, we have
![]() $P\triangleleft M$
iff there is a sound premouse Q and
$P\triangleleft M$
iff there is a sound premouse Q and
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $P\triangleleft Q$
and
$P\triangleleft Q$
and
![]() $\rho _{n+1}^Q=\theta $
and
$\rho _{n+1}^Q=\theta $
and
![]() $M|\theta \trianglelefteq Q$
and Q satisfies
$M|\theta \trianglelefteq Q$
and Q satisfies
![]() $(n+1)$
-condensation. And
$(n+1)$
-condensation. And
![]() $\mathbb {E}^M$
is the stack of all structures of the form
$\mathbb {E}^M$
is the stack of all structures of the form
![]() $\mathcal {S}_m(P)$
for such P and
$\mathcal {S}_m(P)$
for such P and
![]() $m<\omega $
.
$m<\omega $
.
Case 2.
![]() $\theta $
is a cutpoint of M.Footnote
17
$\theta $
is a cutpoint of M.Footnote
17
Use the proof of Corollary 1.5, or an adaptation thereof if
![]() $M=\mathcal {J}(R)$
for some R, combined with 3.4 and 3.5.
$M=\mathcal {J}(R)$
for some R, combined with 3.4 and 3.5.
Case 3.
M has no cutpoint in
![]() $[\theta ,\mathrm {Ord}^M)$
.
$[\theta ,\mathrm {Ord}^M)$
.
Use 1.4.
Case 4.
![]() $\mathrm {cof}^M(\theta )>\omega $
.
$\mathrm {cof}^M(\theta )>\omega $
.
Let
![]() $P\in M$
and
$P\in M$
and
![]() $n<\omega $
be such that P is a sound premouse,
$n<\omega $
be such that P is a sound premouse,
![]() $M|\theta \trianglelefteq P$
,
$M|\theta \trianglelefteq P$
,
![]() $\rho _{n+1}^P=\theta $
, and P satisfies
$\rho _{n+1}^P=\theta $
, and P satisfies
![]() $(n+1)$
-condensation. We claim that
$(n+1)$
-condensation. We claim that
![]() $P\triangleleft M$
; clearly this suffices. If
$P\triangleleft M$
; clearly this suffices. If
![]() $\theta $
is regular in M we can use the proof of case (i), so suppose otherwise; in particular,
$\theta $
is regular in M we can use the proof of case (i), so suppose otherwise; in particular,
![]() $\theta $
is a limit cardinal of M.
$\theta $
is a limit cardinal of M.
We prove that
![]() $P\triangleleft M$
using a phalanx comparison. Let
$P\triangleleft M$
using a phalanx comparison. Let
![]() $Q\triangleleft M$
and
$Q\triangleleft M$
and
![]() $x\in Q$
and
$x\in Q$
and
![]() ${m<\omega }$
be such that P is
${m<\omega }$
be such that P is
![]() $\mathrm {r}\Sigma _m^Q(\{x\})$
; in particular,
$\mathrm {r}\Sigma _m^Q(\{x\})$
; in particular,
![]() $\mathrm {Ord}^P\leq \mathrm {Ord}^Q$
. We must show that
$\mathrm {Ord}^P\leq \mathrm {Ord}^Q$
. We must show that
![]() $P\trianglelefteq Q$
. Suppose not; note that the fact that
$P\trianglelefteq Q$
. Suppose not; note that the fact that
![]() $P\ntrianglelefteq Q$
is first-order over Q (in the parameter x). So we may assume that
$P\ntrianglelefteq Q$
is first-order over Q (in the parameter x). So we may assume that
![]() $x=\emptyset $
(increasing m if needed). Let
$x=\emptyset $
(increasing m if needed). Let
![]() $m+n+5<k<\omega $
and let
$m+n+5<k<\omega $
and let
![]() $\bar {Q}=\mathrm {cHull}_{k+1}^Q(\emptyset )$
. Then
$\bar {Q}=\mathrm {cHull}_{k+1}^Q(\emptyset )$
. Then
![]() $\bar {Q}\triangleleft M$
. Let
$\bar {Q}\triangleleft M$
. Let
![]() $\bar {P}$
be defined over
$\bar {P}$
be defined over
![]() $\bar {Q}$
as P is over Q. Let
$\bar {Q}$
as P is over Q. Let
![]() $\pi :\bar {Q}\to Q$
be the uncollapse, and
$\pi :\bar {Q}\to Q$
be the uncollapse, and
![]() $\pi (\bar {\theta })=\theta $
. Then
$\pi (\bar {\theta })=\theta $
. Then
![]() $\bar {P}$
is
$\bar {P}$
is
![]() $(n+1)$
-sound and
$(n+1)$
-sound and
![]() $\rho _{n+1}^{\bar {P}}=\bar {\theta }$
,
$\rho _{n+1}^{\bar {P}}=\bar {\theta }$
,
![]() $\bar {Q}$
is
$\bar {Q}$
is
![]() $\omega $
-sound and
$\omega $
-sound and
![]() $\rho _{k+1}^{\bar {Q}}=\omega $
,
$\rho _{k+1}^{\bar {Q}}=\omega $
,
![]() $\bar {P}|\bar {\theta }=\bar {Q}|\bar {\theta }$
,
$\bar {P}|\bar {\theta }=\bar {Q}|\bar {\theta }$
,
![]() $\bar {\theta }$
is a cardinal of both models, and
$\bar {\theta }$
is a cardinal of both models, and
![]() $\bar {P}\ntrianglelefteq \bar {Q}$
.
$\bar {P}\ntrianglelefteq \bar {Q}$
.
Define the phalanx
![]() $\mathfrak {P}=((\bar {Q},k,\bar {\theta }),(\bar {P},n),\bar {\theta })$
. By the following claim, a standard comparison argument (comparing
$\mathfrak {P}=((\bar {Q},k,\bar {\theta }),(\bar {P},n),\bar {\theta })$
. By the following claim, a standard comparison argument (comparing
![]() $\mathfrak {P}$
with
$\mathfrak {P}$
with
![]() $\bar {Q}$
) shows that
$\bar {Q}$
) shows that
![]() $\bar {P}\trianglelefteq \bar {Q}$
, a contradiction, completing the proof.
$\bar {P}\trianglelefteq \bar {Q}$
, a contradiction, completing the proof.
Claim 1.
![]() $\mathfrak {P}$
is
$\mathfrak {P}$
is
![]() $(\omega _1+1)$
-iterable.
$(\omega _1+1)$
-iterable.
Proof Let
![]() $\sigma :\bar {P}\to P$
be
$\sigma :\bar {P}\to P$
be
![]() $\pi \!\upharpoonright \!\bar {P}$
. Then
$\pi \!\upharpoonright \!\bar {P}$
. Then
![]() $\sigma \!\upharpoonright \!\bar {\theta }=\pi \!\upharpoonright \!\bar {\theta }$
, and by the choice of k,
$\sigma \!\upharpoonright \!\bar {\theta }=\pi \!\upharpoonright \!\bar {\theta }$
, and by the choice of k,
![]() $\sigma $
is
$\sigma $
is
![]() $\Sigma _{n+5}$
-elementary, so
$\Sigma _{n+5}$
-elementary, so
Let
![]() $\eta =\sup \pi "\bar {\theta }$
. Then
$\eta =\sup \pi "\bar {\theta }$
. Then
![]() $\eta <\theta $
because
$\eta <\theta $
because
![]() $\mathrm {cof}^M(\theta )>\omega $
. Because
$\mathrm {cof}^M(\theta )>\omega $
. Because
![]() $\theta $
is a limit cardinal of M, so is
$\theta $
is a limit cardinal of M, so is
![]() $\eta $
. Let
$\eta $
. Let
and
![]() $\pi ':P'\to P$
be the uncollapse.
$\pi ':P'\to P$
be the uncollapse.
We claim
![]() $P'$
is
$P'$
is
![]() $(n+1)$
-sound,
$(n+1)$
-sound,
![]() $\rho _{n+1}^{P'}=\eta $
and
$\rho _{n+1}^{P'}=\eta $
and
![]() $q=_{\mathrm {def}} p^{P'}_{n+1}=(\pi ')^{-1}(p_{n+1}^P)$
. For
$q=_{\mathrm {def}} p^{P'}_{n+1}=(\pi ')^{-1}(p_{n+1}^P)$
. For
so
![]() $\rho _{n+1}^{P'}\leq \eta $
. But
$\rho _{n+1}^{P'}\leq \eta $
. But
![]() $P'|\eta =M|\eta $
and
$P'|\eta =M|\eta $
and
![]() $P'\in M$
, and as
$P'\in M$
, and as
![]() $\eta $
is an M-cardinal, therefore
$\eta $
is an M-cardinal, therefore
![]() $\rho _{n+1}^{P'}=\eta $
and
$\rho _{n+1}^{P'}=\eta $
and
![]() $p_{n+1}^{P'}\leq q$
. But by line (6),
$p_{n+1}^{P'}\leq q$
. But by line (6),
![]() $(P',q)$
is
$(P',q)$
is
![]() $(n+1)$
-solid (and
$(n+1)$
-solid (and
![]() $\pi '$
maps the
$\pi '$
maps the
![]() $(n+1)$
-solidity witnesses of
$(n+1)$
-solidity witnesses of
![]() $(P',q)$
to the
$(P',q)$
to the
![]() $(n+1)$
-solidity witnesses of P). Therefore
$(n+1)$
-solidity witnesses of P). Therefore
![]() $p_{n+1}^{P'}=q$
and
$p_{n+1}^{P'}=q$
and
![]() $P'$
is
$P'$
is
![]() $(n+1)$
-sound, as desired.
$(n+1)$
-sound, as desired.
So we can apply
![]() $(n+1)$
-condensation to
$(n+1)$
-condensation to
![]() $\pi ':P'\to P$
(by hypothesis on P), and note that it follows that
$\pi ':P'\to P$
(by hypothesis on P), and note that it follows that
![]() $P'\triangleleft M|\theta \trianglelefteq Q\triangleleft M$
.
$P'\triangleleft M|\theta \trianglelefteq Q\triangleleft M$
.
Let
![]() $\sigma ':\bar {P}\to P'$
be the natural factor map. Then
$\sigma ':\bar {P}\to P'$
be the natural factor map. Then
![]() $\sigma '$
is a near n-embedding, and
$\sigma '$
is a near n-embedding, and
![]() $\sigma '\!\upharpoonright \!\bar {\theta }=\pi \!\upharpoonright \!\bar {\theta }$
. Using
$\sigma '\!\upharpoonright \!\bar {\theta }=\pi \!\upharpoonright \!\bar {\theta }$
. Using
![]() $(\pi ,\sigma ')$
, one can lift normal trees on
$(\pi ,\sigma ')$
, one can lift normal trees on
![]() $\mathfrak {P}$
to normal trees on Q, completing the proof.
$\mathfrak {P}$
to normal trees on Q, completing the proof.
Case 5.
![]() $M\models $
“
$M\models $
“
![]() $\theta $
is not a limit of cardinals which are
$\theta $
is not a limit of cardinals which are
![]() $\mathcal {H}_\theta $
-strong”.
$\mathcal {H}_\theta $
-strong”.
This is almost the same as the previous case. Everything is identical until defining
![]() $\eta $
. Set
$\eta $
. Set
![]() $\eta =\pi (\bar {\eta })$
where
$\eta =\pi (\bar {\eta })$
where
![]() $\bar {\eta }$
is some
$\bar {\eta }$
is some
![]() $\bar {Q}$
-cardinal
$\bar {Q}$
-cardinal
![]() $\bar {\eta }<\bar {\theta }$
such that
$\bar {\eta }<\bar {\theta }$
such that
![]() $\bar {\eta }>\kappa $
for all
$\bar {\eta }>\kappa $
for all
![]() $\mathcal {H}_\theta $
-strong cardinals
$\mathcal {H}_\theta $
-strong cardinals
![]() $\kappa $
of M, and the
$\kappa $
of M, and the
![]() $(n+1)$
-solidity witnesses of
$(n+1)$
-solidity witnesses of
![]() $\bar {P}$
are in
$\bar {P}$
are in
![]() $\mathrm {Hull}_{n+1}^{\bar {P}}(\bar {\eta }\cup \{\vec {p}_{n+1}^{\bar {P}}\})$
. (Note we may again assume that
$\mathrm {Hull}_{n+1}^{\bar {P}}(\bar {\eta }\cup \{\vec {p}_{n+1}^{\bar {P}}\})$
. (Note we may again assume that
![]() $\theta $
is singular in M, and hence a limit cardinal of M and
$\theta $
is singular in M, and hence a limit cardinal of M and
![]() $\bar {\theta }$
is a limit cardinal of
$\bar {\theta }$
is a limit cardinal of
![]() $\bar {P}$
. We again get that
$\bar {P}$
. We again get that
![]() $\eta $
is an M-cardinal, though in this case it might not be a limit cardinal of M.) We get
$\eta $
is an M-cardinal, though in this case it might not be a limit cardinal of M.) We get
![]() $\sigma '\!\upharpoonright \!(\bar {\eta }+1)=\pi \!\upharpoonright \!(\bar {\eta }+1)$
, which, by the choice of
$\sigma '\!\upharpoonright \!(\bar {\eta }+1)=\pi \!\upharpoonright \!(\bar {\eta }+1)$
, which, by the choice of
![]() $\bar {\eta }$
, suffices for iterability.
$\bar {\eta }$
, suffices for iterability.
The remaining two cases are more subtle than the previous ones. We (may) now make the:
Assumption 1.
![]() $\theta $
is a singular cardinal of M and M has a cutpoint in
$\theta $
is a singular cardinal of M and M has a cutpoint in
![]() $[\theta ,\mathrm {Ord}^M)$
.
$[\theta ,\mathrm {Ord}^M)$
.
This must of course be incorporated appropriately into the
![]() $\Sigma _4(\{M|\theta \})$
(in case (vi)) and
$\Sigma _4(\{M|\theta \})$
(in case (vi)) and
![]() $\Sigma _3(\{M|\theta \})$
(in case (vii)) definitions one forms from the arguments to follow. But given the definability
$\Sigma _3(\{M|\theta \})$
(in case (vii)) definitions one forms from the arguments to follow. But given the definability
![]() $(\Sigma ,\Lambda )$
established for cases (i) and (iii), this is no problem. (Note here that in case (vii), M does have a cutpoint
$(\Sigma ,\Lambda )$
established for cases (i) and (iii), this is no problem. (Note here that in case (vii), M does have a cutpoint
![]() $\geq \theta $
, so the
$\geq \theta $
, so the
![]() $\Pi _3$
complexity of asserting the non-existence of a cutpoint is not relevant in this case.)
$\Pi _3$
complexity of asserting the non-existence of a cutpoint is not relevant in this case.)
Case 6.
![]() .
.
Work in M and let P be a premouse. Say that P is good iff P is sound,
![]() $M|\theta \trianglelefteq P$
and
$M|\theta \trianglelefteq P$
and
![]() $\rho _\omega ^P=\theta $
. Say that P is excellent iff P is good, M and
$\rho _\omega ^P=\theta $
. Say that P is excellent iff P is good, M and ![]() have the same universe, and
have the same universe, and
![]() $1$
-condensation holds for every
$1$
-condensation holds for every ![]() .
.
By the case hypothesis, M has no largest proper segment, so with Assumption 1, it follows that there are cofinally many excellent
![]() $N\triangleleft M$
. Therefore it suffices to prove the following claim:
$N\triangleleft M$
. Therefore it suffices to prove the following claim:
Claim 1. Let
![]() $P,Q\in M$
be excellent. Then either
$P,Q\in M$
be excellent. Then either
![]() $P\trianglelefteq Q$
or
$P\trianglelefteq Q$
or
![]() $Q\trianglelefteq P$
.
$Q\trianglelefteq P$
.
Proof We may assume
![]() $Q\triangleleft M$
and
$Q\triangleleft M$
and
![]() $\mathrm {Ord}^Q$
is a cutpoint of M, so
$\mathrm {Ord}^Q$
is a cutpoint of M, so ![]() . Define
. Define
![]() $\left <P_n,Q_n\right>_{n<\omega }$
as follows. Let
$\left <P_n,Q_n\right>_{n<\omega }$
as follows. Let
![]() $P_0=P$
and
$P_0=P$
and
![]() $Q_0=Q$
. Given
$Q_0=Q$
. Given
![]() $P_n,Q_n$
, let
$P_n,Q_n$
, let
![]() $Q_{n+1}$
be the least
$Q_{n+1}$
be the least
![]() $N\triangleleft M$
such that N is good,
$N\triangleleft M$
such that N is good,
![]() $Q_n\triangleleft N$
and
$Q_n\triangleleft N$
and
![]() $P_n\in N$
. Given
$P_n\in N$
. Given
![]() $P_n,Q_{n+1}$
, let
$P_n,Q_{n+1}$
, let
![]() $P_{n+1}$
be the least
$P_{n+1}$
be the least ![]() such that R is good,
such that R is good,
![]() $P_n\triangleleft R$
and
$P_n\triangleleft R$
and
![]() $Q_{n+1}\in R$
.
$Q_{n+1}\in R$
.
Let
![]() $\widetilde {P}=\mathrm {stack}_{n<\omega }P_n$
and
$\widetilde {P}=\mathrm {stack}_{n<\omega }P_n$
and
![]() $\widetilde {Q}=\mathrm {stack}_{n<\omega }Q_n$
. Note that
$\widetilde {Q}=\mathrm {stack}_{n<\omega }Q_n$
. Note that
![]() $\widetilde {P}$
and
$\widetilde {P}$
and
![]() $\widetilde {Q}$
have the same universe U (but ostensibly may have different extender sequences). We have
$\widetilde {Q}$
have the same universe U (but ostensibly may have different extender sequences). We have
![]() $\mathrm {Ord}^U<\mathrm {Ord}^M$
by our case hypothesis, as
$\mathrm {Ord}^U<\mathrm {Ord}^M$
by our case hypothesis, as
![]() $\left <P_n,Q_n\right>_{n<\omega }$
is
$\left <P_n,Q_n\right>_{n<\omega }$
is
![]() $\Sigma _2^{\left \lfloor M\right \rfloor }(\{P,Q\})$
.Footnote
18
Now
$\Sigma _2^{\left \lfloor M\right \rfloor }(\{P,Q\})$
.Footnote
18
Now
![]() $\widetilde {P}$
is definable over U from the parameter P, and likewise
$\widetilde {P}$
is definable over U from the parameter P, and likewise
![]() $\widetilde {Q}$
over U from Q; in fact,
$\widetilde {Q}$
over U from Q; in fact,
(Clearly cofinally many segments of
![]() $\widetilde {P}$
satisfy the requirements for premice in
$\widetilde {P}$
satisfy the requirements for premice in ![]() ; but if R is some premouse satisfying these requirements then working in U, we can run the same proof as before to see that
; but if R is some premouse satisfying these requirements then working in U, we can run the same proof as before to see that ![]() .) Also, U has largest cardinal
.) Also, U has largest cardinal
![]() $\theta $
, so
$\theta $
, so ![]() and
and
![]() $M|\mathrm {Ord}^U$
are both passive. So letting
$M|\mathrm {Ord}^U$
are both passive. So letting
![]() $P^+=\mathcal {J}(\widetilde {P})$
and
$P^+=\mathcal {J}(\widetilde {P})$
and
![]() $Q^+=\mathcal {J}(\widetilde {Q})$
, we have
$Q^+=\mathcal {J}(\widetilde {Q})$
, we have ![]() and
and
![]() $Q^+\triangleleft M$
and (because
$Q^+\triangleleft M$
and (because
![]() $\widetilde {P},\widetilde {Q}$
are definable from parameters over U),
$\widetilde {P},\widetilde {Q}$
are definable from parameters over U),
Also because
![]() $\mathrm {Ord}^U$
has cofinality
$\mathrm {Ord}^U$
has cofinality
![]() $\omega $
, definably over U from parameters, we have
$\omega $
, definably over U from parameters, we have
We claim that there is an M-cardinal
![]() $\gamma <\theta $
such that
$\gamma <\theta $
such that
(“
![]() $\mathrm {Hull}$
” denotes the uncollapsed hull), and the transitive collapses
$\mathrm {Hull}$
” denotes the uncollapsed hull), and the transitive collapses
![]() $\bar {P}^+,\bar {Q}^+$
are
$\bar {P}^+,\bar {Q}^+$
are
![]() $1$
-sound and such that
$1$
-sound and such that
![]() $\rho _1^{\bar {P}^+}=\gamma =\rho _1^{\bar {Q}^+}$
. For recalling that
$\rho _1^{\bar {P}^+}=\gamma =\rho _1^{\bar {Q}^+}$
. For recalling that
![]() $\theta $
is a limit cardinal of M, let
$\theta $
is a limit cardinal of M, let
![]() $\gamma <\theta $
be an M-cardinal large enough that, defining
$\gamma <\theta $
be an M-cardinal large enough that, defining
![]() $H,J$
as above, we have
$H,J$
as above, we have
(recall
![]() $w_1^{P^+},w_1^{Q^+}$
are the
$w_1^{P^+},w_1^{Q^+}$
are the
![]() $1$
-solidity witnesses for
$1$
-solidity witnesses for
![]() $P^+,Q^+$
). Then because
$P^+,Q^+$
). Then because
![]() $\gamma $
is an M-cardinal and
$\gamma $
is an M-cardinal and
![]() $w_1^{P^+}\in H$
, we easily have that
$w_1^{P^+}\in H$
, we easily have that
![]() $\rho _1^{\bar {P}^+}=\gamma $
and
$\rho _1^{\bar {P}^+}=\gamma $
and
![]() $\bar {P}^+$
is
$\bar {P}^+$
is
![]() $1$
-sound, and likewise for
$1$
-sound, and likewise for
![]() $\bar {Q}^+$
. And because
$\bar {Q}^+$
. And because
and
![]() $P^+,Q^+$
have the same universe, we have
$P^+,Q^+$
have the same universe, we have
![]() $J\subseteq H$
. Similarly
$J\subseteq H$
. Similarly
![]() $H\subseteq J$
, giving line (7).
$H\subseteq J$
, giving line (7).
By
![]() $1$
-condensation for
$1$
-condensation for
![]() $P^+,Q^+$
(a requirement of excellence), and because
$P^+,Q^+$
(a requirement of excellence), and because
![]() ${\rho _1^{\bar {P}^+}=\gamma =\rho _1^{\bar {Q}^+}}$
is an M-cardinal, we have
${\rho _1^{\bar {P}^+}=\gamma =\rho _1^{\bar {Q}^+}}$
is an M-cardinal, we have
![]() $\bar {P}^+\triangleleft M$
and
$\bar {P}^+\triangleleft M$
and
![]() $\bar {Q}^+\triangleleft M$
. By line (7),
$\bar {Q}^+\triangleleft M$
. By line (7),
![]() $\mathrm {Ord}^{\bar {P}^+}=\mathrm {Ord}^{\bar {Q}^+}$
. Therefore
$\mathrm {Ord}^{\bar {P}^+}=\mathrm {Ord}^{\bar {Q}^+}$
. Therefore
![]() $\bar {P}^+=\bar {Q}^+$
. It easily follows that
$\bar {P}^+=\bar {Q}^+$
. It easily follows that
![]() $\widetilde {P}=\widetilde {Q}$
, giving the claim.
$\widetilde {P}=\widetilde {Q}$
, giving the claim.
Case 7.
![]() and M is eventually constructible.
and M is eventually constructible.
A simplification of the argument in the previous case shows that the collection of all
![]() $R\triangleleft M$
such that
$R\triangleleft M$
such that
![]() $M=\mathcal {J}_\alpha (R)$
for some
$M=\mathcal {J}_\alpha (R)$
for some
![]() $\alpha>0$
, is
$\alpha>0$
, is
![]() $\Pi _2^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
. Regarding the complexity of the case specification, it is
$\Pi _2^{\left \lfloor M\right \rfloor }(\{M|\theta \})$
. Regarding the complexity of the case specification, it is
![]() $\Sigma _3^{\left \lfloor M\right \rfloor }$
to assert “M is eventually constructible”, as it is equivalent to
$\Sigma _3^{\left \lfloor M\right \rfloor }$
to assert “M is eventually constructible”, as it is equivalent to
(M fails to be eventually constructible iff M is closed under sharps).
This completes all cases and hence, the proof of the theorem.
Definition 3.12. Let M be a transitive structure. Let ![]() be a premouse with
be a premouse with ![]() . The inductive condensation stack of M above
. The inductive condensation stack of M above ![]() is the stack of premice in M, extending
is the stack of premice in M, extending ![]() , satisfying the inductive definition used in the proof of 3.11.
, satisfying the inductive definition used in the proof of 3.11.
Of course, the inductive condensation stack S could have
![]() $\mathrm {Ord}^S<\mathrm {Ord}^M$
. But if M is a
$\mathrm {Ord}^S<\mathrm {Ord}^M$
. But if M is a
![]() $(0,\omega _1+1)$
-iterable tractable premouse and
$(0,\omega _1+1)$
-iterable tractable premouse and ![]() then
then
![]() $M=S$
.
$M=S$
.
Remark 3.13. In case (iii) of the preceding proof, it appeared that we used 1.4 for extenders E generated by
![]() $\theta \cup t$
for some finite set t of generators (in order that we can represent arbitrary segments
$\theta \cup t$
for some finite set t of generators (in order that we can represent arbitrary segments
![]() $R\triangleleft M|\theta ^{+M}$
). Actually, it suffices to consider only extenders E such that
$R\triangleleft M|\theta ^{+M}$
). Actually, it suffices to consider only extenders E such that
![]() $\nu _E=\theta $
(and
$\nu _E=\theta $
(and
![]() $\mathcal {H}_\theta ^M\subseteq \mathrm {Ult}(M,E)$
etc.). For we claim that (under the case hypothesis) there are unboundedly many
$\mathcal {H}_\theta ^M\subseteq \mathrm {Ult}(M,E)$
etc.). For we claim that (under the case hypothesis) there are unboundedly many
![]() $\beta <\mathrm {Ord}^M$
such that
$\beta <\mathrm {Ord}^M$
such that
![]() $M|\beta $
is active with an extender E such that
$M|\beta $
is active with an extender E such that
![]() $\nu _E=\theta $
; clearly this suffices.
$\nu _E=\theta $
; clearly this suffices.
For let
![]() $Q\triangleleft M$
be such that
$Q\triangleleft M$
be such that
![]() $\rho _\omega ^Q=\theta $
and let
$\rho _\omega ^Q=\theta $
and let
![]() $\alpha $
be least such that
$\alpha $
be least such that
![]() $\alpha>\mathrm {Ord}^Q$
and
$\alpha>\mathrm {Ord}^Q$
and
![]() $M|\alpha $
is active with extender F and
$M|\alpha $
is active with extender F and
![]() $\kappa =\mathrm {cr}(F)<\theta $
. We claim that
$\kappa =\mathrm {cr}(F)<\theta $
. We claim that
![]() $\nu _F=\theta $
. So suppose that
$\nu _F=\theta $
. So suppose that
![]() $\theta <\nu _F$
. Easily by the ISC,
$\theta <\nu _F$
. Easily by the ISC,
![]() $\theta $
is the largest cardinal of
$\theta $
is the largest cardinal of
![]() $M|\alpha $
. So F is type 2. Let
$M|\alpha $
. So F is type 2. Let
![]() $E=F\!\upharpoonright \!\theta $
, let
$E=F\!\upharpoonright \!\theta $
, let
![]() $U_E=\mathrm {Ult}_0(M,E)$
,
$U_E=\mathrm {Ult}_0(M,E)$
,
![]() $U_F=\mathrm {Ult}_0(M,F)$
and
$U_F=\mathrm {Ult}_0(M,F)$
and
![]() $\pi :U_E\to U_F$
the standard factor map. So
$\pi :U_E\to U_F$
the standard factor map. So
![]() $\mathrm {cr}(\pi )$
is the least generator
$\mathrm {cr}(\pi )$
is the least generator
![]() $\gamma $
of F with
$\gamma $
of F with
![]() $\gamma \geq \theta $
.
$\gamma \geq \theta $
.
Suppose
![]() $\gamma =\theta $
. Then
$\gamma =\theta $
. Then
![]() $\theta $
is a limit cardinal of M and
$\theta $
is a limit cardinal of M and
![]() $U_E$
, so
$U_E$
, so
![]() $\pi (\theta )>\theta ^{+U_F}=\mathrm {lh}(F)$
. By the ISC,
$\pi (\theta )>\theta ^{+U_F}=\mathrm {lh}(F)$
. By the ISC,
![]() $\kappa $
is
$\kappa $
is
![]() $\mathcal {H}_\xi $
-strong in
$\mathcal {H}_\xi $
-strong in
![]() $U_E$
for each
$U_E$
for each
![]() $\xi <\theta $
. Therefore
$\xi <\theta $
. Therefore
![]() $\kappa $
is
$\kappa $
is
![]() $\mathcal {H}_\xi $
-strong in
$\mathcal {H}_\xi $
-strong in
![]() $U_F$
for each
$U_F$
for each
![]() $\xi <\pi (\theta )$
. But then by the ISC, there are unboundedly many
$\xi <\pi (\theta )$
. But then by the ISC, there are unboundedly many
![]() $\zeta <\theta ^{+U_F}$
indexing an extender G with
$\zeta <\theta ^{+U_F}$
indexing an extender G with
![]() $\mathrm {cr}(G)=\kappa $
, and since
$\mathrm {cr}(G)=\kappa $
, and since
![]() $Q\triangleleft U_F|\theta ^{+U_F}$
, this contradicts the minimality of F.
$Q\triangleleft U_F|\theta ^{+U_F}$
, this contradicts the minimality of F.
So
![]() $\gamma>\theta $
. Because
$\gamma>\theta $
. Because
![]() $\theta ^{+U_E}=\mathrm {lh}(E)<\mathrm {lh}(F)=\theta ^{+U_F}$
, we have
$\theta ^{+U_E}=\mathrm {lh}(E)<\mathrm {lh}(F)=\theta ^{+U_F}$
, we have
![]() $\gamma =\mathrm {lh}(E)$
and
$\gamma =\mathrm {lh}(E)$
and
![]() $\pi (\gamma )=\mathrm {lh}(F)$
. But
$\pi (\gamma )=\mathrm {lh}(F)$
. But
![]() $E\in \mathbb {E}^{U_F}$
, so by reflection, there are unboundedly many
$E\in \mathbb {E}^{U_F}$
, so by reflection, there are unboundedly many
![]() $\xi <\mathrm {lh}(E)$
such that
$\xi <\mathrm {lh}(E)$
such that
![]() $M|\xi $
is active with an extender G with
$M|\xi $
is active with an extender G with
![]() $\mathrm {cr}(G)=\kappa $
, and so the same holds of
$\mathrm {cr}(G)=\kappa $
, and so the same holds of
![]() $\pi (\mathrm {lh}(E))=\mathrm {lh}(F)$
, again contradicting the minimality of F.
$\pi (\mathrm {lh}(E))=\mathrm {lh}(F)$
, again contradicting the minimality of F.
Remark 3.14. Let M be passive,
![]() $(0,\omega _1+1)$
-iterable, satisfying “
$(0,\omega _1+1)$
-iterable, satisfying “
![]() $\omega _1$
exists” and
$\omega _1$
exists” and
![]() $\theta =\mathrm {lgcd}(M)$
. We sketch, in a further case, the identification of M from parameter
$\theta =\mathrm {lgcd}(M)$
. We sketch, in a further case, the identification of M from parameter
![]() $M|\theta $
over
$M|\theta $
over
![]() $\left \lfloor M\right \rfloor $
. However, here we do not know whether the case specification itself is uniformly definable over
$\left \lfloor M\right \rfloor $
. However, here we do not know whether the case specification itself is uniformly definable over
![]() $\left \lfloor M\right \rfloor $
as above. Say that M is
$\left \lfloor M\right \rfloor $
as above. Say that M is ![]() -bounded iff
-bounded iff
![]() $\mathrm {Hull}_1^M(\alpha \cup \{x\})$
is bounded in
$\mathrm {Hull}_1^M(\alpha \cup \{x\})$
is bounded in
![]() $\mathrm {Ord}^M$
for every
$\mathrm {Ord}^M$
for every
![]() $\alpha <\rho _1^M$
and
$\alpha <\rho _1^M$
and
![]() $x\in M$
. Suppose that M is
$x\in M$
. Suppose that M is
![]() $1$
-sound and
$1$
-sound and
![]() $\rho _1^M>\omega $
, and either M is eventually constructible or M is not
$\rho _1^M>\omega $
, and either M is eventually constructible or M is not ![]() -bounded. Then M is definable from
-bounded. Then M is definable from
![]() $M|\theta $
over
$M|\theta $
over
![]() $\left \lfloor M\right \rfloor $
.
$\left \lfloor M\right \rfloor $
.
To see this, we argue much as in the last two cases of 3.11. We may make Assumption 1. If M is eventually constructible things are easier (using then either the argument from case (vii) of 3.11 if ![]() , or a variant of the argument to follow otherwise), so we leave this case to the reader, and suppose otherwise. So M is closed under sharps and has no largest proper segment. The difference to case (vi) of 3.11 is that now, when we define
, or a variant of the argument to follow otherwise), so we leave this case to the reader, and suppose otherwise. So M is closed under sharps and has no largest proper segment. The difference to case (vi) of 3.11 is that now, when we define
![]() $\widetilde {P},\widetilde {Q}$
, we might have
$\widetilde {P},\widetilde {Q}$
, we might have
![]() $\left \lfloor M\right \rfloor =\left \lfloor \widetilde {P}\right \rfloor =\left \lfloor \widetilde {Q}\right \rfloor $
. Let
$\left \lfloor M\right \rfloor =\left \lfloor \widetilde {P}\right \rfloor =\left \lfloor \widetilde {Q}\right \rfloor $
. Let
![]() $P\in M$
be good (good defined as before). Say that P is outstanding iff P satisfies the conditions of excellence from before, and letting
$P\in M$
be good (good defined as before). Say that P is outstanding iff P satisfies the conditions of excellence from before, and letting ![]() , then
, then
![]() $P^*$
is
$P^*$
is
![]() $1$
-sound,
$1$
-sound,
![]() $\rho _1^{P^*}>\omega $
,
$\rho _1^{P^*}>\omega $
,
![]() $P^*$
is not
$P^*$
is not ![]() -bounded,
-bounded,
![]() $1$
-condensation holds for
$1$
-condensation holds for
![]() $P^*$
, and for all
$P^*$
, and for all
![]() $R\trianglelefteq P^*$
, if
$R\trianglelefteq P^*$
, if
then for all sufficiently large
![]() $\gamma <\rho $
,
$\gamma <\rho $
,
(so
![]() $1$
-condensation applies to the uncollapse map). By 2.4, all sufficiently large good
$1$
-condensation applies to the uncollapse map). By 2.4, all sufficiently large good
![]() $Q\triangleleft M$
are outstanding; we take Q such.
$Q\triangleleft M$
are outstanding; we take Q such.
Let
![]() $P\in M$
be outstanding. We claim
$P\in M$
be outstanding. We claim
![]() $\rho _1^{P^*}=\rho _1^{M}$
. For suppose
$\rho _1^{P^*}=\rho _1^{M}$
. For suppose
![]() $\rho _1^{P^*}<\rho _1^M$
. Let
$\rho _1^{P^*}<\rho _1^M$
. Let
![]() $\alpha \in [\rho _1^{P^*},\rho _1^M)$
be large enough that
$\alpha \in [\rho _1^{P^*},\rho _1^M)$
be large enough that
is unbounded in
![]() $\mathrm {Ord}^M$
(using non-
$\mathrm {Ord}^M$
(using non-![]() -boundedness) and
-boundedness) and
![]() $P,p_1^{P^*}\in H$
. Then
$P,p_1^{P^*}\in H$
. Then
![]() $P'\in H$
for cofinally many
$P'\in H$
for cofinally many
![]() $P'\triangleleft P^*$
. For given
$P'\triangleleft P^*$
. For given
![]() $\eta _0,\eta _1\in H\cap \mathrm {Ord}^M$
such that there is a good
$\eta _0,\eta _1\in H\cap \mathrm {Ord}^M$
such that there is a good
![]() $P'\triangleleft P^*$
with
$P'\triangleleft P^*$
with
![]() $\eta _0\leq \mathrm {Ord}^{P'}$
and
$\eta _0\leq \mathrm {Ord}^{P'}$
and
![]() $P'\in M|\eta _1$
, then the least good
$P'\in M|\eta _1$
, then the least good
![]() $P"\triangleleft P^*$
such that
$P"\triangleleft P^*$
such that
![]() $\eta _0\leq \mathrm {Ord}^{P"}$
, is in H. (Recall that
$\eta _0\leq \mathrm {Ord}^{P"}$
, is in H. (Recall that ![]() is the stack of all good Q such that
is the stack of all good Q such that
![]() $P\trianglelefteq Q$
, P is a cutpoint of Q and all countable elementary substructures of Q in M have transitive collapse
$P\trianglelefteq Q$
, P is a cutpoint of Q and all countable elementary substructures of Q in M have transitive collapse ![]() . But in order to identify the desired
. But in order to identify the desired
![]() $P"$
, it suffices to restrict attention to all countable elementary substructures of
$P"$
, it suffices to restrict attention to all countable elementary substructures of
![]() $P"$
in
$P"$
in
![]() $M|(\eta _1+\omega ^2)$
; recall here that M is closed under sharps, so
$M|(\eta _1+\omega ^2)$
; recall here that M is closed under sharps, so
![]() $\eta _1+\omega ^2<\mathrm {Ord}^M$
. This is because
$\eta _1+\omega ^2<\mathrm {Ord}^M$
. This is because
![]() $P'\in M|\eta _1$
, and we can run the argument which shows that
$P'\in M|\eta _1$
, and we can run the argument which shows that
![]() $P'\trianglelefteq P"$
or
$P'\trianglelefteq P"$
or
![]() $P"\trianglelefteq P'$
working in
$P"\trianglelefteq P'$
working in
![]() $M_1|(\eta _1+\omega ^2)$
.) It follows that
$M_1|(\eta _1+\omega ^2)$
.) It follows that
But
![]() $P^*$
is
$P^*$
is
![]() $1$
-sound and
$1$
-sound and
![]() $\left \lfloor P^*\right \rfloor =\left \lfloor M\right \rfloor $
, so
$\left \lfloor P^*\right \rfloor =\left \lfloor M\right \rfloor $
, so
![]() $M=H$
, contradicting the fact that
$M=H$
, contradicting the fact that
![]() $\alpha <\rho _1^M$
. So
$\alpha <\rho _1^M$
. So
![]() $\rho _1^M\leq \rho _1^{P^*}$
and the converse is likewise.
$\rho _1^M\leq \rho _1^{P^*}$
and the converse is likewise.
The rest is much like the last part of the argument used in case (vi), but we might get
![]() $\widetilde {P}=P^*$
and
$\widetilde {P}=P^*$
and
![]() $\widetilde {Q}=M$
, in which case there is a wrinkle. If this occurs, choose
$\widetilde {Q}=M$
, in which case there is a wrinkle. If this occurs, choose
![]() $\alpha <\rho _1^M=\rho _1^{P^*}$
such that
$\alpha <\rho _1^M=\rho _1^{P^*}$
such that
by arguing as in the previous paragraph, and such that the transitive collapses
![]() $\bar {P},\bar {Q}$
of the hulls are
$\bar {P},\bar {Q}$
of the hulls are
![]() $1$
-sound (using 2.4 and excellence if
$1$
-sound (using 2.4 and excellence if
![]() $\rho _1^M=\kappa ^{+M}$
). Then by
$\rho _1^M=\kappa ^{+M}$
). Then by
![]() $1$
-condensation we get
$1$
-condensation we get
![]() $\bar {P}=\bar {Q}$
, so
$\bar {P}=\bar {Q}$
, so
![]() $P=Q$
.
$P=Q$
.
Corollary 3.15. Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse satisfying either
$(0,\omega _1+1)$
-iterable premouse satisfying either
![]() $\mathrm {PS}$
or
$\mathrm {PS}$
or
![]() $\mathrm {ZFC}^-+$
“
$\mathrm {ZFC}^-+$
“
![]() $\omega _1$
exists”. Suppose that either
$\omega _1$
exists”. Suppose that either
![]() $:$
$:$
-
(i)
 is
is
 $(\omega ,\omega _1+1)$
-iterable in M,Footnote
19
or
$(\omega ,\omega _1+1)$
-iterable in M,Footnote
19
or -
(ii)
 is built by theFootnote
20
maximal fully backgrounded
is built by theFootnote
20
maximal fully backgrounded
 $L[\mathbb {E}]$
-construction of M using background extenders
$L[\mathbb {E}]$
-construction of M using background extenders
 $E\in \mathbb {E}^M$
such that
$E\in \mathbb {E}^M$
such that
 $\nu _E$
is an M-cardinal.
$\nu _E$
is an M-cardinal.
Then
![]() $:$
$:$
-
1.
 $\mathbb {E}^M$
is definable over
$\mathbb {E}^M$
is definable over
 $\left \lfloor M\right \rfloor $
without parameters,
$\left \lfloor M\right \rfloor $
without parameters, -
2.
 $\left \lfloor M\right \rfloor =\mathrm {Hull}^{\left \lfloor M\right \rfloor }(\mathrm {Ord}^M)$
, and
$\left \lfloor M\right \rfloor =\mathrm {Hull}^{\left \lfloor M\right \rfloor }(\mathrm {Ord}^M)$
, and -
3. if assumption (i) holds and
 $M\models \mathrm {PS}$
then
$M\models \mathrm {PS}$
then
 $\left \lfloor M\right \rfloor =\mathrm {OD}^{\left \lfloor M\right \rfloor }$
.Footnote
21
$\left \lfloor M\right \rfloor =\mathrm {OD}^{\left \lfloor M\right \rfloor }$
.Footnote
21
Proof If assumption (i) holds, then all three conclusions follow easily from 3.11.
If assumption (ii) holds, by 1.2, if
![]() $E\in M$
then [
$E\in M$
then [
![]() $E\in \mathbb {E}^M$
and
$E\in \mathbb {E}^M$
and
![]() $\nu _E$
is an M-cardinal] iff
$\nu _E$
is an M-cardinal] iff
![]() $M\models \text {"}E$
is a countably complete extender,
$M\models \text {"}E$
is a countably complete extender,
![]() $\nu _E$
is a cardinal and
$\nu _E$
is a cardinal and
![]() $\mathcal {H}_{\nu _E}\subseteq \mathrm {Ult}(V,E)$
”. So the
$\mathcal {H}_{\nu _E}\subseteq \mathrm {Ult}(V,E)$
”. So the
![]() $L[\mathbb {E}]$
-construction using these background extenders is definable over
$L[\mathbb {E}]$
-construction using these background extenders is definable over
![]() $\left \lfloor M\right \rfloor $
without parameters, so
$\left \lfloor M\right \rfloor $
without parameters, so ![]() is likewise definable, so conclusions 1 and 2 follow easily from 3.11.Footnote
22
is likewise definable, so conclusions 1 and 2 follow easily from 3.11.Footnote
22
Recall that
![]() $M_{\mathrm {wlim}}$
is the least proper class mouse with a Woodin limit of Woodins. Part (ii) of the previous corollary gives:
$M_{\mathrm {wlim}}$
is the least proper class mouse with a Woodin limit of Woodins. Part (ii) of the previous corollary gives:
Corollary 3.16.
![]() $\left \lfloor M_{\mathrm {wlim}}\right \rfloor \models $
“
$\left \lfloor M_{\mathrm {wlim}}\right \rfloor \models $
“
![]() $V=\mathrm {HOD}$
”.
$V=\mathrm {HOD}$
”.
There are of course many variants of this corollary. Using the background construction of [Reference Schlutzenberg9] in place of the background construction used above, one gets that
![]() $\left \lfloor M\right \rfloor \models $
“
$\left \lfloor M\right \rfloor \models $
“
![]() $V=\mathrm {HOD}$
” where M is, for example, the least proper class mouse with a
$V=\mathrm {HOD}$
” where M is, for example, the least proper class mouse with a
![]() $\lambda $
which is a limit of Woodins and strong cardinals.
$\lambda $
which is a limit of Woodins and strong cardinals.
4 Direct condensation stack in
 $M[G]$
$M[G]$
In this section we prove the following theorem, using a variant of the inductive condensation stack:
Theorem 4.1. Let M be a
![]() $(0,\omega _1+1)$
-iterable premouse satisfying
$(0,\omega _1+1)$
-iterable premouse satisfying
![]() $\mathrm {PS}$
. Let
$\mathrm {PS}$
. Let
![]() ${\theta <\mathrm {Ord}^M}$
be a regular cardinal of M and
${\theta <\mathrm {Ord}^M}$
be a regular cardinal of M and
![]() $\mathbb P\in M|\theta $
be a poset. Let G be
$\mathbb P\in M|\theta $
be a poset. Let G be
![]() $(M,\mathbb P)$
-generic. Then
$(M,\mathbb P)$
-generic. Then
![]() $\mathbb {E}^M$
is definable over
$\mathbb {E}^M$
is definable over
![]() $M[G]$
from the parameter
$M[G]$
from the parameter
![]() $M|\theta $
.
$M|\theta $
.
Proof Work in
![]() $M[G]$
. It suffices to give a definition of
$M[G]$
. It suffices to give a definition of
![]() $M|\eta ^{+M}$
from the parameter
$M|\eta ^{+M}$
from the parameter
![]() $M|\theta $
, uniformly in M-regular cardinals
$M|\theta $
, uniformly in M-regular cardinals
![]() $\eta \geq \theta $
. Note that the Jensen stack over
$\eta \geq \theta $
. Note that the Jensen stack over
![]() $M|\eta $
is exactly
$M|\eta $
is exactly
![]() $M|\eta ^+$
, and this structure satisfies standard condensation facts. (But if
$M|\eta ^+$
, and this structure satisfies standard condensation facts. (But if
![]() $\eta>\theta $
, we don’t have the parameter
$\eta>\theta $
, we don’t have the parameter
![]() $M|\eta $
available to refer to.)
$M|\eta $
available to refer to.)
Say that a premouse P is excellent iff
![]() $M|\theta \trianglelefteq P$
,
$M|\theta \trianglelefteq P$
,
![]() $\mathrm {Ord}^P=\eta $
, the Jensen stack
$\mathrm {Ord}^P=\eta $
, the Jensen stack
![]() $P^+$
over P has height
$P^+$
over P has height
![]() $\eta ^+$
,
$\eta ^+$
,
![]() $P^+$
satisfies standard condensation facts, and there is
$P^+$
satisfies standard condensation facts, and there is
![]() $\mathbb Q\in P|\theta $
and a
$\mathbb Q\in P|\theta $
and a
![]() $(P,\mathbb Q)$
-generic filter h such that
$(P,\mathbb Q)$
-generic filter h such that
![]() $P^+[h]$
has universe
$P^+[h]$
has universe
![]() $\mathcal {H}_{\eta ^+}$
.
$\mathcal {H}_{\eta ^+}$
.
Clearly the following claim completes the proof:
Claim 1.
![]() $M|\eta $
is the unique excellent premouse.
$M|\eta $
is the unique excellent premouse.
Proof Clearly
![]() $N=M|\eta $
is excellent, as witnessed by
$N=M|\eta $
is excellent, as witnessed by
![]() $\mathbb P,g$
.
$\mathbb P,g$
.
So let R also be excellent, as witnessed by
![]() $\mathbb Q,h$
. Define a sequence
$\mathbb Q,h$
. Define a sequence
![]() $\left <N_n,R_n\right>_{n<\omega }$
as follows. Let
$\left <N_n,R_n\right>_{n<\omega }$
as follows. Let
![]() $N_0=N$
and
$N_0=N$
and
![]() $R_0=R$
. Given
$R_0=R$
. Given
![]() $N_n,R_n$
, let
$N_n,R_n$
, let
![]() $N_{n+1}$
be the least
$N_{n+1}$
be the least
![]() $N'$
such that
$N'$
such that
![]() $N_n\triangleleft N'\triangleleft N^+$
and
$N_n\triangleleft N'\triangleleft N^+$
and
![]() $\rho _\omega ^{N'}=\eta $
and
$\rho _\omega ^{N'}=\eta $
and
![]() $R_n,h\in N'[g]$
; then let
$R_n,h\in N'[g]$
; then let
![]() $R_{n+1}$
be the least
$R_{n+1}$
be the least
![]() $R'$
such that
$R'$
such that
![]() $R_n\triangleleft R'\triangleleft R^+$
and
$R_n\triangleleft R'\triangleleft R^+$
and
![]() $\rho _\omega ^{R'}=\eta $
and
$\rho _\omega ^{R'}=\eta $
and
![]() $N_{n+1},g\in R'[h]$
. Let
$N_{n+1},g\in R'[h]$
. Let
![]() $N_\omega =\mathrm {stack}_{n<\omega }N_n$
and
$N_\omega =\mathrm {stack}_{n<\omega }N_n$
and
![]() $\widetilde {N}=\mathcal {J}(N_\omega )$
, and
$\widetilde {N}=\mathcal {J}(N_\omega )$
, and
![]() $R_\omega ,\widetilde {R}$
likewise. Then
$R_\omega ,\widetilde {R}$
likewise. Then
![]() $\widetilde {N}\triangleleft N^+$
and
$\widetilde {N}\triangleleft N^+$
and
![]() $\widetilde {R}\triangleleft R^+$
. Note that
$\widetilde {R}\triangleleft R^+$
. Note that
![]() $N_\omega [g]$
and
$N_\omega [g]$
and
![]() $R_\omega [h]$
have the same universe U, and
$R_\omega [h]$
have the same universe U, and
![]() $N_\omega ,R_\omega $
are both definable from parameters over U (via the Jensen stack). Hence,
$N_\omega ,R_\omega $
are both definable from parameters over U (via the Jensen stack). Hence,
![]() $\mathcal {J}(N_\omega [g])$
and
$\mathcal {J}(N_\omega [g])$
and
![]() $\mathcal {J}(R_\omega [h])$
and
$\mathcal {J}(R_\omega [h])$
and
![]() $\widetilde {N}[g]$
and
$\widetilde {N}[g]$
and
![]() $\widetilde {R}[h]$
all have the same universe
$\widetilde {R}[h]$
all have the same universe
![]() $\widetilde {U}=\mathcal {J}(U)$
.
$\widetilde {U}=\mathcal {J}(U)$
.
Now
![]() $\widetilde {N},\widetilde {R}$
both satisfy standard
$\widetilde {N},\widetilde {R}$
both satisfy standard
![]() $1$
-condensation facts. Let
$1$
-condensation facts. Let
![]() $\gamma <\theta $
be a cardinal of the models
$\gamma <\theta $
be a cardinal of the models
![]() $N,N[g],R[h],R$
such that
$N,N[g],R[h],R$
such that
![]() $\mathbb P,\mathbb Q$
have cardinality
$\mathbb P,\mathbb Q$
have cardinality
![]() $\leq \gamma $
in
$\leq \gamma $
in
![]() $N,R$
respectively.
$N,R$
respectively.
Subclaim 1.1. For all
![]() $x\in \widetilde {U}$
there is
$x\in \widetilde {U}$
there is
![]() $q\in [\mathrm {Ord}^{\widetilde {U}}]^{<\omega }$
such that the hulls
$q\in [\mathrm {Ord}^{\widetilde {U}}]^{<\omega }$
such that the hulls
![]() $H,H',J,J'$
all contain the same ordinals, where
$H,H',J,J'$
all contain the same ordinals, where
and moreover,
![]() $\mathbb P\in H$
,
$\mathbb P\in H$
,
![]() $\mathbb Q\in J$
,
$\mathbb Q\in J$
,
![]() $x\in H'=J'$
, and the transitive collapses
$x\in H'=J'$
, and the transitive collapses
![]() $C,D$
of
$C,D$
of
![]() $H,J$
respectively are sound.
$H,J$
respectively are sound.
Assuming the subclaim, let
![]() $\pi :C\to H$
and
$\pi :C\to H$
and
![]() $\sigma :D\to J$
be the uncollapses. Then by
$\sigma :D\to J$
be the uncollapses. Then by
![]() $1$
-condensation,
$1$
-condensation,
![]() $C\triangleleft N|\theta $
and
$C\triangleleft N|\theta $
and
![]() $D\triangleleft R|\theta $
, and hence
$D\triangleleft R|\theta $
, and hence
![]() $C=D$
(as
$C=D$
(as
![]() $N|\theta =R|\theta $
and
$N|\theta =R|\theta $
and
![]() $\mathrm {Ord}^C=\mathrm {Ord}^D$
), and
$\mathrm {Ord}^C=\mathrm {Ord}^D$
), and
![]() $\pi \!\upharpoonright \!\mathrm {Ord}=\sigma \!\upharpoonright \!\mathrm {Ord}$
. But then
$\pi \!\upharpoonright \!\mathrm {Ord}=\sigma \!\upharpoonright \!\mathrm {Ord}$
. But then
![]() $\widetilde {N}=\widetilde {R}$
and
$\widetilde {N}=\widetilde {R}$
and
![]() $N=R$
, as desired.
$N=R$
, as desired.
Proof of Subclaim
Use a simple variant of the proof of 2.3 to choose q, running an algorithm much as there, but simultaneously for both models
![]() $\widetilde {N},\widetilde {R}$
, and using the “
$\widetilde {N},\widetilde {R}$
, and using the “
![]() $\Sigma _1$
-definability of the
$\Sigma _1$
-definability of the
![]() $\Sigma _1$
-forcing relation” to see that
$\Sigma _1$
-forcing relation” to see that
![]() $H,H'$
contain the same ordinals (and likewise
$H,H'$
contain the same ordinals (and likewise
![]() $J,J'$
), and choosing elements of q large enough to ensure that
$J,J'$
), and choosing elements of q large enough to ensure that
![]() $H'=J'$
and
$H'=J'$
and
![]() $\mathbb P\in H$
, etc.
$\mathbb P\in H$
, etc.
Here are some more details: Given
![]() $q\!\upharpoonright \! i$
and
$q\!\upharpoonright \! i$
and
![]() $\gamma _i$
much as in the proof of 2.3, first select some
$\gamma _i$
much as in the proof of 2.3, first select some
![]() $q^{\prime }_i$
satisfying the requirements much as before with respect to
$q^{\prime }_i$
satisfying the requirements much as before with respect to
![]() $\widetilde {N}$
(hence with
$\widetilde {N}$
(hence with
![]() $\gamma _i<q^{\prime }_i<(\gamma _i^+)^{\widetilde {U}}$
), and with
$\gamma _i<q^{\prime }_i<(\gamma _i^+)^{\widetilde {U}}$
), and with
![]() $q^{\prime }_i$
large enough that
$q^{\prime }_i$
large enough that
![]() $\mathbb P\cup \{\mathbb P\}\subseteq $
the relevant hulls of
$\mathbb P\cup \{\mathbb P\}\subseteq $
the relevant hulls of
![]() $\widetilde {N}$
(note this condition holds trivially unless
$\widetilde {N}$
(note this condition holds trivially unless
![]() $\gamma _i<\theta $
) and
$\gamma _i<\theta $
) and
![]() $x,N_\omega ,R_\omega ,g,h$
are in the relevant hulls of
$x,N_\omega ,R_\omega ,g,h$
are in the relevant hulls of
![]() $\widetilde {U}$
. Then choose
$\widetilde {U}$
. Then choose
![]() $q_i$
with
$q_i$
with
![]() $q^{\prime }_i<q_i<(\gamma _i^+)^{\widetilde {U}}$
and much as before with respect to
$q^{\prime }_i<q_i<(\gamma _i^+)^{\widetilde {U}}$
and much as before with respect to
![]() $\widetilde {R}$
. In this manner it is easy to arrange that
$\widetilde {R}$
. In this manner it is easy to arrange that
![]() $q_i$
works. We leave the rest to the reader.
$q_i$
works. We leave the rest to the reader.
This completes the proof of the subclaim, claim, and theorem.
Definition 4.2. Let M be a transitive structure satisfying
![]() $\mathrm {PS}$
. Work in M. Let P be a premouse with
$\mathrm {PS}$
. Work in M. Let P be a premouse with
![]() $\mathrm {Ord}^P$
regular. For a regular cardinal
$\mathrm {Ord}^P$
regular. For a regular cardinal
![]() $\eta \geq \mathrm {Ord}^P$
, define
$\eta \geq \mathrm {Ord}^P$
, define
![]() $\eta $
-excellent premice (relative to
$\eta $
-excellent premice (relative to
![]() $P,\eta $
) as in the proof above (there we have
$P,\eta $
) as in the proof above (there we have
![]() $P=M|\theta $
). The direct condensation stack of M above P is the stack S of all
$P=M|\theta $
). The direct condensation stack of M above P is the stack S of all
![]() $\eta $
-excellent premice, for all such
$\eta $
-excellent premice, for all such
![]() $\eta $
, as far as this is a well-defined stack.
$\eta $
, as far as this is a well-defined stack.
Remark 4.3. As a special case of the previous theorem, we get a shorter proof that if a mouse M satisfies
![]() $\mathrm {PS}$
, then
$\mathrm {PS}$
, then
![]() $\mathbb {E}^M$
is definable over
$\mathbb {E}^M$
is definable over
![]() $\left \lfloor M\right \rfloor $
from the parameter
$\left \lfloor M\right \rfloor $
from the parameter
![]() $M|\omega _1^M$
. Note that the proof also easily adapts to the case that M has a largest cardinal
$M|\omega _1^M$
. Note that the proof also easily adapts to the case that M has a largest cardinal
![]() $\lambda $
, assuming that
$\lambda $
, assuming that
![]() $\lambda $
is M-regular. However, for the singular case (most importantly
$\lambda $
is M-regular. However, for the singular case (most importantly
![]() $\mathrm {cof}^M(\lambda )=\omega $
) we need the earlier methods.
$\mathrm {cof}^M(\lambda )=\omega $
) we need the earlier methods.
5 A simplified fine structure
In [Reference Mitchell and Steel1], Mitchell–Steel fine structure is introduced, which makes use of the parameters
![]() $u_n$
. We introduce a simplified fine structure here which avoids the parameters
$u_n$
. We introduce a simplified fine structure here which avoids the parameters
![]() $u_n$
, and show that in fact, the two fine structures are equivalent: we get the same notions of soundness, the same projecta and standard parameters, etc.
$u_n$
, and show that in fact, the two fine structures are equivalent: we get the same notions of soundness, the same projecta and standard parameters, etc.
Definition 5.1. Let N be a premouse. Given
![]() $X\subseteq N$
,
$X\subseteq N$
,
![]() $\mathrm {Hull}_{k+1}^N(X)$
denotes the substructure of N whose elements are those
$\mathrm {Hull}_{k+1}^N(X)$
denotes the substructure of N whose elements are those
![]() $z\in N$
such that there is
$z\in N$
such that there is
![]() $\vec {x}\in X^{<\omega }$
and an
$\vec {x}\in X^{<\omega }$
and an
![]() $\mathrm {r}\Sigma _{k+1}$
formula
$\mathrm {r}\Sigma _{k+1}$
formula
![]() $\varphi $
such that z is the unique
$\varphi $
such that z is the unique
![]() $z'\in N$
such that
$z'\in N$
such that
![]() $N\models \varphi (\vec {x},z')$
. And
$N\models \varphi (\vec {x},z')$
. And
![]() $\mathrm {cHull}_{k+1}^N(X)$
denotes its transitive collapse, assuming this is well-defined. Also let
$\mathrm {cHull}_{k+1}^N(X)$
denotes its transitive collapse, assuming this is well-defined. Also let
![]() $\mathrm {Th}_{k+1}^N(X)$
be the
$\mathrm {Th}_{k+1}^N(X)$
be the
![]() $\mathrm {r}\Sigma _{k+1}$
theoryFootnote
23
of N in parameters in X.
$\mathrm {r}\Sigma _{k+1}$
theoryFootnote
23
of N in parameters in X.
Definition 5.2 (Minimal Skolem terms).
Let
![]() $\varphi $
be an
$\varphi $
be an
![]() $\mathrm {r}\Sigma _{k+1}$
formula of
$\mathrm {r}\Sigma _{k+1}$
formula of
![]() $n+1<\omega $
free variables
$n+1<\omega $
free variables
![]() $v_0,\ldots ,v_n$
. The minimal Skolem term associated with
$v_0,\ldots ,v_n$
. The minimal Skolem term associated with
![]() $\varphi $
is denoted
$\varphi $
is denoted
![]() $\mathrm {m}\tau _\varphi $
, and has n variables
$\mathrm {m}\tau _\varphi $
, and has n variables
![]() $v_1,\ldots ,v_n$
.
$v_1,\ldots ,v_n$
.
Let R be a k-sound premouse with
![]() $\rho _k^R>\omega $
. Let
$\rho _k^R>\omega $
. Let
![]() $q\in [\rho _0^R]^{<\omega }$
such that (i) if
$q\in [\rho _0^R]^{<\omega }$
such that (i) if
![]() $k>0$
then
$k>0$
then
![]() $R=\mathrm {Hull}_k^R(\rho ^R_k\cup \{q\})$
and (ii) if
$R=\mathrm {Hull}_k^R(\rho ^R_k\cup \{q\})$
and (ii) if
![]() $q\neq \emptyset $
then
$q\neq \emptyset $
then
![]() $\rho ^R_k\leq \min (q)$
. We define the partial function
$\rho ^R_k\leq \min (q)$
. We define the partial function
If
![]() $k=0$
then
$k=0$
then
![]() $\mathrm {m}\tau _{\varphi ,q}^R$
is just the usual Skolem function associated with
$\mathrm {m}\tau _{\varphi ,q}^R$
is just the usual Skolem function associated with
![]() $\varphi $
(such that the graph of
$\varphi $
(such that the graph of
![]() $\mathrm {m}\tau _\varphi ^R$
is uniformly
$\mathrm {m}\tau _\varphi ^R$
is uniformly
![]() $\mathrm {r}\Sigma _1^R$
), with inputs substituting for
$\mathrm {r}\Sigma _1^R$
), with inputs substituting for
![]() $v_1,\ldots ,v_n$
and output for
$v_1,\ldots ,v_n$
and output for
![]() $v_0$
. (Note
$v_0$
. (Note
![]() $q=\emptyset $
in this case.)
$q=\emptyset $
in this case.)
Suppose
![]() $k>0$
. Let
$k>0$
. Let
![]() $\vec {x}=(x_1,\ldots ,x_n)\in \mathfrak {C}_0(R)^n$
. If
$\vec {x}=(x_1,\ldots ,x_n)\in \mathfrak {C}_0(R)^n$
. If
![]() $\mathfrak {C}_0(R)\models \neg \exists v_0\ \varphi (v_0,\vec {x})$
, then
$\mathfrak {C}_0(R)\models \neg \exists v_0\ \varphi (v_0,\vec {x})$
, then
![]() $\mathrm {m}\tau _{\varphi ,q}^R(\vec {x})$
is undefined.
$\mathrm {m}\tau _{\varphi ,q}^R(\vec {x})$
is undefined.
Suppose
![]() $\mathfrak {C}_0(R)\models \exists v_0\ \varphi (v_0,\vec {x})$
. Let
$\mathfrak {C}_0(R)\models \exists v_0\ \varphi (v_0,\vec {x})$
. Let
![]() $\tau _\varphi $
be the basic Skolem term associated with
$\tau _\varphi $
be the basic Skolem term associated with
![]() $\varphi $
(see [Reference Mitchell and Steel1, 2.3.3]). Recall that
$\varphi $
(see [Reference Mitchell and Steel1, 2.3.3]). Recall that
![]() $\tau _\varphi ^R(\vec {x})$
is the
$\tau _\varphi ^R(\vec {x})$
is the
![]() $<_R$
-least y such that
$<_R$
-least y such that
![]() $\mathfrak {C}_0(R)\models \varphi (y,\vec {x})$
. For
$\mathfrak {C}_0(R)\models \varphi (y,\vec {x})$
. For
![]() $\beta <\rho _k^R$
, let
$\beta <\rho _k^R$
, let
![]() $(\tau _\varphi )^\beta $
be defined over R as in the proof of [Reference Mitchell and Steel1, 2.10], with q specified above. Let
$(\tau _\varphi )^\beta $
be defined over R as in the proof of [Reference Mitchell and Steel1, 2.10], with q specified above. Let
![]() $\beta _0$
be the least
$\beta _0$
be the least
![]() $\beta $
such that
$\beta $
such that
![]() $(\tau _\varphi )^\beta (\vec {x})$
is defined. Then define
$(\tau _\varphi )^\beta (\vec {x})$
is defined. Then define
Lemma 5.3. The graph of
![]() $\mathrm {m}\tau _{\varphi ,q}^R$
is
$\mathrm {m}\tau _{\varphi ,q}^R$
is
![]() $\mathrm {r}\Sigma _{k+1}^R(\{q\})$
, recursively uniformly in
$\mathrm {r}\Sigma _{k+1}^R(\{q\})$
, recursively uniformly in
![]() $\varphi ,R,q$
(for
$\varphi ,R,q$
(for
![]() $R,q$
as in 5.2).
$R,q$
as in 5.2).
Given
![]() $\mathrm {r}\Sigma _{k+1}$
formulas
$\mathrm {r}\Sigma _{k+1}$
formulas
![]() $\varphi ,\psi _0,\ldots ,\psi _{n-1}$
, with
$\varphi ,\psi _0,\ldots ,\psi _{n-1}$
, with
![]() $\varphi $
of n free variables and
$\varphi $
of n free variables and
![]() $\psi _i$
of
$\psi _i$
of
![]() $n_i+1$
free variables, the relation over
$n_i+1$
free variables, the relation over
![]() $\mathfrak {C}_0(R)$
,
$\mathfrak {C}_0(R)$
,
 $$ \begin{align*} \mathfrak{C}_0(R)&\models\varrho(\vec{x}_0,\ldots,\vec{x}_{n-1})\iff \\ & \big(\forall i[\vec{x}_i\in\mathrm{dom}(\mathrm{m}\tau^R_{\psi_i,q})]\big)\wedge \mathfrak{C}_0(R)\models\varphi(\mathrm{m}\tau_{\psi_0,q}(\vec{x}_0),\ldots,\mathrm{m}\tau_{\psi_{n-1},q}(\vec{x}_{n-1} )), \end{align*} $$
$$ \begin{align*} \mathfrak{C}_0(R)&\models\varrho(\vec{x}_0,\ldots,\vec{x}_{n-1})\iff \\ & \big(\forall i[\vec{x}_i\in\mathrm{dom}(\mathrm{m}\tau^R_{\psi_i,q})]\big)\wedge \mathfrak{C}_0(R)\models\varphi(\mathrm{m}\tau_{\psi_0,q}(\vec{x}_0),\ldots,\mathrm{m}\tau_{\psi_{n-1},q}(\vec{x}_{n-1} )), \end{align*} $$
is
![]() $\mathrm {r}\Sigma _{k+1}(\{q\})$
, uniformly in
$\mathrm {r}\Sigma _{k+1}(\{q\})$
, uniformly in
![]() $R,q$
as in 5.2, and moreover, there is a recursive function passing from
$R,q$
as in 5.2, and moreover, there is a recursive function passing from
![]() $\varphi ,\psi _0,\ldots ,\psi _{n-1}$
to an
$\varphi ,\psi _0,\ldots ,\psi _{n-1}$
to an
![]() $\mathrm {r}\Sigma _{k+1}$
formula for
$\mathrm {r}\Sigma _{k+1}$
formula for
![]() $\varrho $
.
$\varrho $
.
Therefore minimal Skolem terms are effectively closed under composition. That is, for example, there is a recursive function passing from formulas
![]() $\varphi ,\psi $
, each of two free variables
$\varphi ,\psi $
, each of two free variables
![]() $v_0,v_1$
, to
$v_0,v_1$
, to
![]() $\varrho $
, of the same free variables, such that for all relevant
$\varrho $
, of the same free variables, such that for all relevant
![]() $R,q$
, we have
$R,q$
, we have
Likewise for compositions involving larger numbers of variables.
Note that the basic Skolem terms referred to in the following lemma were recalled in Definition 5.2.
Lemma 5.4. Let
![]() $R,q$
be as in 5.2,
$R,q$
be as in 5.2,
![]() $X\subseteq \mathfrak {C}_0(R)$
and
$X\subseteq \mathfrak {C}_0(R)$
and
 $$ \begin{align*} H_1&=\mathrm{Hull}_{k+1}^R(X\cup\{q\}),\\ H_2&=\big\{\mathrm{m}\tau^R_{\varphi,q}(\vec{x})\bigm|\varphi\text{ is }\mathrm{r}\Sigma_{k+1}\ \&\ \vec{x}\in X^{<\omega}\big\},\\ H_3&=\text{ the closure of }X\cup\{q\}\text{ under the basic } \mathrm{r}\Sigma_{k+1}\text{-Skolem terms.} \end{align*} $$
$$ \begin{align*} H_1&=\mathrm{Hull}_{k+1}^R(X\cup\{q\}),\\ H_2&=\big\{\mathrm{m}\tau^R_{\varphi,q}(\vec{x})\bigm|\varphi\text{ is }\mathrm{r}\Sigma_{k+1}\ \&\ \vec{x}\in X^{<\omega}\big\},\\ H_3&=\text{ the closure of }X\cup\{q\}\text{ under the basic } \mathrm{r}\Sigma_{k+1}\text{-Skolem terms.} \end{align*} $$
Then
![]() $H_1=H_2=H_3$
.
$H_1=H_2=H_3$
.
Proof The main thing is to see that
![]() $H_3\subseteq H_2$
. For this, see the proof of [Reference Mitchell and Steel1, 2.10], combined with (for example) the observation that if
$H_3\subseteq H_2$
. For this, see the proof of [Reference Mitchell and Steel1, 2.10], combined with (for example) the observation that if
![]() $\vec {x}\in X^{<\omega }$
and
$\vec {x}\in X^{<\omega }$
and
![]() $y\in H_2$
and
$y\in H_2$
and
![]() $R\models \exists z\ \big [z<_R y\wedge \varphi (q,\vec {x},z)\big ]$
, then there is
$R\models \exists z\ \big [z<_R y\wedge \varphi (q,\vec {x},z)\big ]$
, then there is
![]() $z\in H_2$
such that
$z\in H_2$
such that
![]() $z<_R y$
and
$z<_R y$
and
![]() $R\models \varphi (q,\vec {x},z)$
; this is by 5.3. Applying this observation finitely many times shows that
$R\models \varphi (q,\vec {x},z)$
; this is by 5.3. Applying this observation finitely many times shows that
![]() $\tau ^R_\varphi (q,\vec {x})\in H_2$
.
$\tau ^R_\varphi (q,\vec {x})\in H_2$
.
Definition 5.5. For
![]() $k<\omega $
, the terminology k-u-sound, k-u-universal, etc., mean just what k-sound, k-universal, etc., mean in [Reference Mitchell and Steel1, Section 2].Footnote
24
Let N be a k-u-sound premouse. We define
$k<\omega $
, the terminology k-u-sound, k-u-universal, etc., mean just what k-sound, k-universal, etc., mean in [Reference Mitchell and Steel1, Section 2].Footnote
24
Let N be a k-u-sound premouse. We define
![]() $\rho _k^N=\rho _k(N)$
,
$\rho _k^N=\rho _k(N)$
,
![]() $p_k(N)=p_k^N$
,
$p_k(N)=p_k^N$
,
![]() $u_k(N)=u_k^N$
,
$u_k(N)=u_k^N$
,
![]() $\rho _{k+1}^N=\rho _{k+1}(N)$
and
$\rho _{k+1}^N=\rho _{k+1}(N)$
and
![]() $p_{k+1}(N)=p_{k+1}^N$
as in [Reference Mitchell and Steel1, Definition 2.8.1]. We also define
$p_{k+1}(N)=p_{k+1}^N$
as in [Reference Mitchell and Steel1, Definition 2.8.1]. We also define
![]() $\widetilde {p}_0(N)=\widetilde {p}_0^N=\emptyset $
and if
$\widetilde {p}_0(N)=\widetilde {p}_0^N=\emptyset $
and if
![]() $k>0$
, define
$k>0$
, define
![]() $\widetilde {p}_k(N)=\widetilde {p}^N_k=r$
where
$\widetilde {p}_k(N)=\widetilde {p}^N_k=r$
where
![]() $p_k^N=(r,u_{k-1}^N)$
. Given
$p_k^N=(r,u_{k-1}^N)$
. Given
![]() $u\in \mathfrak {C}_0(N)$
,
$u\in \mathfrak {C}_0(N)$
,
![]() $\widetilde {p}\in [\rho _0^N]^{<\omega }$
and
$\widetilde {p}\in [\rho _0^N]^{<\omega }$
and
![]() $\alpha \in \widetilde {p}$
, define the
$\alpha \in \widetilde {p}$
, define the
![]() $(k+1)$
-solidity-witness for
$(k+1)$
-solidity-witness for
![]() $(N,\widetilde {p},u)$
at
$(N,\widetilde {p},u)$
at
![]() $\alpha $
, denoted
$\alpha $
, denoted
![]() $W_{k+1}^N(\widetilde {p},u,\alpha )$
, by
$W_{k+1}^N(\widetilde {p},u,\alpha )$
, by
We say N is
![]() $(k+1)$
-u-solidity-witnessed iff
$(k+1)$
-u-solidity-witnessed iff
Recall here that in [Reference Mitchell and Steel1, Definition 2.8.2] and [Reference Steel13, Definition 2.15], the adjective
![]() $(k+1)$
-solid, as applied to premice N, means something different to
$(k+1)$
-solid, as applied to premice N, means something different to
![]() $(k+1)$
-u-solidity-witnessed.
$(k+1)$
-u-solidity-witnessed.
Remark 5.6. Recall that
![]() $p_{1}^N=(\widetilde {p}_1^N,\emptyset )$
and
$p_{1}^N=(\widetilde {p}_1^N,\emptyset )$
and
![]() $\widetilde {p}_1^N\in [\rho _0^N]^{<\omega }$
. Suppose that N is k-sound,
$\widetilde {p}_1^N\in [\rho _0^N]^{<\omega }$
. Suppose that N is k-sound,
![]() $p_k^N=(\widetilde {p}_k^N,u)$
and
$p_k^N=(\widetilde {p}_k^N,u)$
and
![]() $s=\widetilde {p}_k^N\in [\rho _{k-1}^N]^{<\omega }$
,
$s=\widetilde {p}_k^N\in [\rho _{k-1}^N]^{<\omega }$
,
![]() $\mathrm {lh}(s)=\ell $
and
$\mathrm {lh}(s)=\ell $
and
![]() $b_0,\ldots ,b_{\ell -1}$
are the k-u-solidity witnesses for
$b_0,\ldots ,b_{\ell -1}$
are the k-u-solidity witnesses for
![]() $(N,s,u)$
(that is,
$(N,s,u)$
(that is,
![]() $b_i=W_{k}^N(s,u,\alpha _i)$
for each
$b_i=W_{k}^N(s,u,\alpha _i)$
for each
![]() $i<\ell $
, where
$i<\ell $
, where
![]() $s=\{\alpha _0>\alpha _1>\cdots >\alpha _{\ell -1}\}$
). Recall that
$s=\{\alpha _0>\alpha _1>\cdots >\alpha _{\ell -1}\}$
). Recall that
![]() $p_{k+1}^N$
has form
$p_{k+1}^N$
has form
![]() $(r,u_k^N)$
where:
$(r,u_k^N)$
where:
-
– if
 $\rho _{k-1}^N<\rho _0^N$
then
$\rho _{k-1}^N<\rho _0^N$
then
 $u_k^N=(s,u,b_0,\ldots ,b_{\ell -1},\rho _{k-1}^N)$
, and
$u_k^N=(s,u,b_0,\ldots ,b_{\ell -1},\rho _{k-1}^N)$
, and -
– if
 $\rho _{k-1}^N=\rho _0^N$
then
$\rho _{k-1}^N=\rho _0^N$
then
 $u_k^N=(s,u,b_0,\ldots ,b_{\ell -1})$
.
$u_k^N=(s,u,b_0,\ldots ,b_{\ell -1})$
.
(Cf. [Reference Mitchell and Steel1, Definition 2.8.1], but note that we are discussing
![]() $p_{k+1}$
here, not
$p_{k+1}$
here, not
![]() $p_k$
.)
$p_k$
.)
Definition 5.7. For N a premouse, define
![]() $q_k=q_k^N$
, k-q-universality, k-q-solidity and k-q-soundness for
$q_k=q_k^N$
, k-q-universality, k-q-solidity and k-q-soundness for
![]() $k\in [0,\omega )$
, recursively as follows. The definitions are actually made uniformly in premice N.
$k\in [0,\omega )$
, recursively as follows. The definitions are actually made uniformly in premice N.
Define
![]() $q_0^N=\emptyset $
and say that N is
$q_0^N=\emptyset $
and say that N is
![]() $0$
-q-universal,
$0$
-q-universal,
![]() $0$
-q-solid and
$0$
-q-solid and
![]() $0$
-q-sound.
$0$
-q-sound.
Suppose
![]() $q_0,\ldots ,q_k$
have been defined and N is k-q-sound and k-u-sound.
$q_0,\ldots ,q_k$
have been defined and N is k-q-sound and k-u-sound.
Now if
![]() $k\geq 1$
then suppose by induction that
$k\geq 1$
then suppose by induction that
Let
![]() $q_{k+1}$
be the
$q_{k+1}$
be the
![]() $<_{\mathrm {lex}}$
-least
$<_{\mathrm {lex}}$
-least
![]() $q\in [\mathrm {Ord}]^{<\omega }$
such thatFootnote
25
$q\in [\mathrm {Ord}]^{<\omega }$
such thatFootnote
25
Define the
![]() $(k+1)$
th core
$(k+1)$
th core
![]() $\mathfrak {C}_{k+1}(N)$
of N as
$\mathfrak {C}_{k+1}(N)$
of N as
and the
![]() $(k+1)$
th core map
$(k+1)$
th core map
![]() $\pi :C\to N$
to be the uncollapse map. It will follow from Theorem 5.8 that C is k-q-sound and k-u-sound and if
$\pi :C\to N$
to be the uncollapse map. It will follow from Theorem 5.8 that C is k-q-sound and k-u-sound and if
![]() $k\geq 1$
then
$k\geq 1$
then
So
![]() $q_{k+1}^C$
is defined. Say N is
$q_{k+1}^C$
is defined. Say N is
![]() $(k+1)$
-q-universal iff
$(k+1)$
-q-universal iff
![]() $\mathcal {P}(\rho _{k+1}^N)\cap C=\mathcal {P}(\rho _{k+1}^N)\cap N$
.
$\mathcal {P}(\rho _{k+1}^N)\cap C=\mathcal {P}(\rho _{k+1}^N)\cap N$
.
Given
![]() $u\in \mathfrak {C}_0(N)$
and
$u\in \mathfrak {C}_0(N)$
and
![]() $q\in [\rho _0^N]^{<\omega }$
and
$q\in [\rho _0^N]^{<\omega }$
and
![]() $\alpha \in q$
, define
$\alpha \in q$
, define
![]() $W_{k+1}^N(q,u,\alpha )$
exactly as in line (8) in Definition 5.5, with
$W_{k+1}^N(q,u,\alpha )$
exactly as in line (8) in Definition 5.5, with
![]() $\widetilde {p}=q$
.Footnote
26
$\widetilde {p}=q$
.Footnote
26
We say
![]() $(q,u)$
is
$(q,u)$
is
![]() $(k+1)$
-solid for N iff
$(k+1)$
-solid for N iff
![]() $W_{k+1}^N(q,u,\alpha )\in N$
for each
$W_{k+1}^N(q,u,\alpha )\in N$
for each
![]() $\alpha \in q$
. We say N is
$\alpha \in q$
. We say N is
![]() $(k+1)$
-q-solid iff
$(k+1)$
-q-solid iff
![]() $(q_{k+1},q_k)$
is
$(q_{k+1},q_k)$
is
![]() $(k+1)$
-solid for N.Footnote
27
We say N is
$(k+1)$
-solid for N.Footnote
27
We say N is
![]() $(k+1)$
-q-sound iff N is
$(k+1)$
-q-sound iff N is
![]() $(k+1)$
-q-solid and
$(k+1)$
-q-solid and
The theorem below establishes the equivalence between standard Mitchell–Steel fine structure (u-soundness, etc.) and the fine structure introduced here (q-soundness, etc.). In part 3 we show that the parameters provided by
![]() $u^N_k$
automatically get into the relevant hulls, so that the direct placement of the
$u^N_k$
automatically get into the relevant hulls, so that the direct placement of the
![]() $u^N_k$
in those hulls in [Reference Mitchell and Steel1] was superfluous.
$u^N_k$
in those hulls in [Reference Mitchell and Steel1] was superfluous.
Theorem 5.8. Let
![]() $k<\omega $
. Let N be a premouse. Then
$k<\omega $
. Let N be a premouse. Then
![]() $:$
$:$
-
1. N is k-q-sound iff N is k-u-sound.
If N is k-q-sound and
![]() $\omega <\rho _k^N$
then
$\omega <\rho _k^N$
then
![]() $:$
$:$
-
2.
 $\widetilde {p}_i^N=q_i^N$
for all
$\widetilde {p}_i^N=q_i^N$
for all
 $i\leq k$
.
$i\leq k$
. -
3. Let
 $X\subseteq N$
, let
$X\subseteq N$
, let
 $C=\mathrm {cHull}_{k+1}^N(X\cup \{q_k^N\})$
and
$C=\mathrm {cHull}_{k+1}^N(X\cup \{q_k^N\})$
and
 $\pi :C\to N$
be the uncollapse. Then
$\pi :C\to N$
be the uncollapse. Then
 $:$
$:$
-
(i) C is a k-u-sound premouse,
-
(ii)
 $\pi $
is a near k-u-embeddingFootnote
28
$\pi $
is a near k-u-embeddingFootnote
28
 $;$
therefore if
$;$
therefore if
 $\rho _k^C<\rho _0^C$
then
$\rho _k^C<\rho _0^C$
then
 $\pi (\rho _k^C)\geq \rho _k^N$
and
$\pi (\rho _k^C)\geq \rho _k^N$
and
 $\pi "\rho _k^C\subseteq \rho _k^N$
,
$\pi "\rho _k^C\subseteq \rho _k^N$
, -
(iii)
 $\pi (W_i^C(q_i^C,q_{i-1}^C,\alpha ))=W_i^N(q_i^N,q_{i-1}^N,\pi (\alpha ))$
for all
$\pi (W_i^C(q_i^C,q_{i-1}^C,\alpha ))=W_i^N(q_i^N,q_{i-1}^N,\pi (\alpha ))$
for all
 $i\in [1,k]$
and
$i\in [1,k]$
and
 ${\alpha \in q_i^C}$
,
${\alpha \in q_i^C}$
, -
(iv)
 $\pi (u_k^C)=u_k^N\in H$
.
$\pi (u_k^C)=u_k^N\in H$
.
-
-
4. We have
 $:$
$:$
-
–
 $\widetilde {p}_{k+1}^N=q_{k+1}^N$
,
$\widetilde {p}_{k+1}^N=q_{k+1}^N$
, -
– N is
 $(k+1)$
-u-solidity-witnessed iff N is
$(k+1)$
-u-solidity-witnessed iff N is
 $(k+1)$
-q-solid,Footnote
29
$(k+1)$
-q-solid,Footnote
29
-
– N is
 $(k+1)$
-u-universal iff N is
$(k+1)$
-u-universal iff N is
 $(k+1)$
-q-universal, and
$(k+1)$
-q-universal, and -
– N is
 $(k+1)$
-u-sound iff N is
$(k+1)$
-u-sound iff N is
 $(k+1)$
-q-sound.
$(k+1)$
-q-sound.
-
Proof We prove the proposition by induction on k. For
![]() $k=0$
it is easy. Assume
$k=0$
it is easy. Assume
![]() $k>0$
and the lemma holds at all
$k>0$
and the lemma holds at all
![]() $k'<k$
. Parts 1 and 2 are trivial by induction (by part 4). So consider part 3. Let
$k'<k$
. Parts 1 and 2 are trivial by induction (by part 4). So consider part 3. Let
![]() $H=\mathrm {rg}(\pi )$
. Note that
$H=\mathrm {rg}(\pi )$
. Note that
![]() $X\cup \{q_k^N\}\subseteq H$
and if
$X\cup \{q_k^N\}\subseteq H$
and if
![]() $\vec {x}\in H$
and
$\vec {x}\in H$
and
![]() $y\in \mathrm {Hull}_{k+1}^N(\{\vec {x}\})$
then
$y\in \mathrm {Hull}_{k+1}^N(\{\vec {x}\})$
then
![]() $y\in H$
. Now we prove:
$y\in H$
. Now we prove:
Claim 1. Let
![]() $i\leq k$
. Then
$i\leq k$
. Then
![]() $q_i^N\in H$
and if
$q_i^N\in H$
and if
![]() $i<k$
and
$i<k$
and
![]() $\rho _i^N<\rho _0^N$
then
$\rho _i^N<\rho _0^N$
then
![]() $\rho _i^N\in H$
.
$\rho _i^N\in H$
.
Proof We prove the claim by induction on i. It is trivial for
![]() $i=0$
and
$i=0$
and
![]() $i=k$
(since
$i=k$
(since
![]() $q_0^N=\emptyset $
and we put
$q_0^N=\emptyset $
and we put
![]() $q_k^N\in H$
directly). Suppose
$q_k^N\in H$
directly). Suppose
![]() $0<i<k$
and the claim holds for all
$0<i<k$
and the claim holds for all
![]() $i'<i$
.
$i'<i$
.
We show
![]() $q_i^N\in H$
. So assume
$q_i^N\in H$
. So assume
![]() $n=\mathrm {lh}(q_i^N)>0$
. Note that
$n=\mathrm {lh}(q_i^N)>0$
. Note that
![]() $q_i^N$
is the unique
$q_i^N$
is the unique
![]() ${q\in [\mathrm {Ord}]^{<\omega }}$
such that:
${q\in [\mathrm {Ord}]^{<\omega }}$
such that:
-
(i)
 $N=\mathrm {Hull}^N_i(\min (q)\cup \{q, q_{i-1}^N\})$
and
$N=\mathrm {Hull}^N_i(\min (q)\cup \{q, q_{i-1}^N\})$
and -
(ii)
 $(q,q_{i-1}^N)$
is i-solid for N and
$(q,q_{i-1}^N)$
is i-solid for N and -
(iii)
 $\mathrm {lh}(q)=n$
.
$\mathrm {lh}(q)=n$
.
Now each of the statements (i)–(iii) are
![]() $\mathrm {r}\Sigma _{k+1}^N$
assertions of q (in no parameters, but the
$\mathrm {r}\Sigma _{k+1}^N$
assertions of q (in no parameters, but the
![]() $\mathrm {r}\Sigma _{k+1}$
formulas used depend on
$\mathrm {r}\Sigma _{k+1}$
formulas used depend on
![]() $(\mathrm {lh}(q_0^N),\ldots ,\mathrm {lh}(q_i^N)=n)$
), and hence,
$(\mathrm {lh}(q_0^N),\ldots ,\mathrm {lh}(q_i^N)=n)$
), and hence,
![]() $\{q_i^N\}$
is
$\{q_i^N\}$
is
![]() $\mathrm {r}\Sigma _{k+1}^N$
, so
$\mathrm {r}\Sigma _{k+1}^N$
, so
![]() $q_i^N\in H$
. If
$q_i^N\in H$
. If
![]() $i=1$
, this is straightforward. If
$i=1$
, this is straightforward. If
![]() $i>1$
, then by (another) induction, we can refer to
$i>1$
, then by (another) induction, we can refer to
![]() $q_j^N$
for each
$q_j^N$
for each
![]() $j<i$
, since we already know that
$j<i$
, since we already know that
![]() $\{q_j^N\}$
is
$\{q_j^N\}$
is
![]() $\mathrm {r}\Sigma _{k+1}^N$
. And for
$\mathrm {r}\Sigma _{k+1}^N$
. And for
![]() $i>1$
, since N is
$i>1$
, since N is
![]() $(i-1)$
-q-sound,
$(i-1)$
-q-sound,
So by 5.4, statement (i) just asserts “
![]() $\forall x\in N\ \big [$
there is
$\forall x\in N\ \big [$
there is
![]() $\vec {\beta }\in \min (q)^{<\omega }$
and an
$\vec {\beta }\in \min (q)^{<\omega }$
and an
![]() $\mathrm {r}\Sigma _i$
formula
$\mathrm {r}\Sigma _i$
formula
![]() $\varphi $
such that
$\varphi $
such that
![]() $x=\mathrm {m}\tau _{\varphi ,(q_{i-1}^N,q_{i-2}^N)}(\vec {\beta },q)\big ]$
”, which is therefore
$x=\mathrm {m}\tau _{\varphi ,(q_{i-1}^N,q_{i-2}^N)}(\vec {\beta },q)\big ]$
”, which is therefore
![]() $\mathrm {r}\Sigma _{k+1}^N$
(recall
$\mathrm {r}\Sigma _{k+1}^N$
(recall
![]() $i<k$
). So
$i<k$
). So
![]() $\{q_i^N\}$
is
$\{q_i^N\}$
is
![]() $\mathrm {r}\Sigma _{k+1}^N$
, as required.
$\mathrm {r}\Sigma _{k+1}^N$
, as required.
Now if
![]() $i<k$
and
$i<k$
and
![]() $\rho _i^N<\rho _0^N$
then by induction,
$\rho _i^N<\rho _0^N$
then by induction,
![]() $\rho ^N_i$
is the least
$\rho ^N_i$
is the least
![]() $\rho $
with
$\rho $
with
So as above and in the proof of 5.4, if
![]() $\rho _i^N<\mathrm {Ord}^N$
then
$\rho _i^N<\mathrm {Ord}^N$
then
![]() $\rho ^N_i\in H$
.Footnote
30
$\rho ^N_i\in H$
.Footnote
30
Claim 2. If
![]() $\varphi $
is
$\varphi $
is
![]() $\mathrm {r}\Sigma _{k+1}$
and
$\mathrm {r}\Sigma _{k+1}$
and
![]() $\vec {x}\in H$
and
$\vec {x}\in H$
and
![]() $N\models \exists y\ \varphi (\vec {x},y)$
then
$N\models \exists y\ \varphi (\vec {x},y)$
then
![]() $\exists y\in H$
such that
$\exists y\in H$
such that
![]() $N\models \varphi (\vec {x},y)$
.
$N\models \varphi (\vec {x},y)$
.
Proof Let
![]() $q=\{q_k^N,q_{k-1}^N\}$
. Since
$q=\{q_k^N,q_{k-1}^N\}$
. Since
![]() $q\in H$
and
$q\in H$
and
![]() $N=\mathrm {Hull}_k^N(\rho _k^N\cup \{q\})$
, 5.4 applies and yields the claim.
$N=\mathrm {Hull}_k^N(\rho _k^N\cup \{q\})$
, 5.4 applies and yields the claim.
We have
![]() $H=\mathrm {Hull}^N_i(H)$
for each
$H=\mathrm {Hull}^N_i(H)$
for each
![]() $i\leq k+1$
. Therefore by induction, C is
$i\leq k+1$
. Therefore by induction, C is
![]() $(k-1)$
-sound,
$(k-1)$
-sound,
![]() $\pi $
is a near
$\pi $
is a near
![]() $(k-1)$
-u-embedding, and so on. Combined with Claim 1, this also gives that if
$(k-1)$
-u-embedding, and so on. Combined with Claim 1, this also gives that if
![]() $\rho _{k-1}^C<\rho _0^C$
then
$\rho _{k-1}^C<\rho _0^C$
then
![]() $\pi (\rho _{k-1}^C)=\rho _{k-1}^N<\rho _0^N$
, and if
$\pi (\rho _{k-1}^C)=\rho _{k-1}^N<\rho _0^N$
, and if
![]() $\rho _{k-1}^C=\rho _0^C$
then
$\rho _{k-1}^C=\rho _0^C$
then
![]() $\rho _{k-1}^N=\rho _0^N$
. By this and Claim 2 it is straightforward to see that
$\rho _{k-1}^N=\rho _0^N$
. By this and Claim 2 it is straightforward to see that
![]() $\pi "\rho _k^C\subseteq \rho _k^N$
and if
$\pi "\rho _k^C\subseteq \rho _k^N$
and if
![]() $\rho _k^C<\rho _0^C$
then
$\rho _k^C<\rho _0^C$
then
![]() $\pi (\rho _k^C)\geq \rho _k^N$
. Moreover,
$\pi (\rho _k^C)\geq \rho _k^N$
. Moreover,
and
![]() $\pi $
is
$\pi $
is
![]() $\mathrm {r}\Sigma _{k+1}$
elementary. To see that
$\mathrm {r}\Sigma _{k+1}$
elementary. To see that
![]() $q_k^C=\pi ^{-1}(q_k^N)$
, we therefore just need that
$q_k^C=\pi ^{-1}(q_k^N)$
, we therefore just need that
![]() $(\pi ^{-1}(q_k^N),q_{k-1}^C)$
is k-q-solid for C. For this it suffices to know that C has the appropriate generalized solidity witnesses; see [Reference Zeman14, Section 1.12]. But this follows from the fact that N has generalized solidity witnesses for
$(\pi ^{-1}(q_k^N),q_{k-1}^C)$
is k-q-solid for C. For this it suffices to know that C has the appropriate generalized solidity witnesses; see [Reference Zeman14, Section 1.12]. But this follows from the fact that N has generalized solidity witnesses for
![]() $(q_k^N,q_{k-1}^N)$
in
$(q_k^N,q_{k-1}^N)$
in
![]() $\mathrm {rg}(\pi )$
, which follows from Claim 2.
$\mathrm {rg}(\pi )$
, which follows from Claim 2.
We have now established that C is k-q-sound, so by induction, C is k-u-sound, giving 3(i). For part 3(ii), it just remains to see that
![]() $\pi (p_k^C)=p_k^N$
. (We already know that
$\pi (p_k^C)=p_k^N$
. (We already know that
![]() $C,N$
are k-u-sound,
$C,N$
are k-u-sound,
![]() $\pi $
is an
$\pi $
is an
![]() $\mathrm {r}\Sigma _{k+1}$
-elementary near
$\mathrm {r}\Sigma _{k+1}$
-elementary near
![]() $(k-1)$
-u-embedding which preserves
$(k-1)$
-u-embedding which preserves
![]() $\rho _{k-1}$
, and
$\rho _{k-1}$
, and
![]() $\pi "\rho _{k}^C\subseteq \rho _k^N$
.) Recall that
$\pi "\rho _{k}^C\subseteq \rho _k^N$
.) Recall that
![]() $p_k^C=(\widetilde {p}_k^C,u_{k-1}^C)$
and
$p_k^C=(\widetilde {p}_k^C,u_{k-1}^C)$
and
![]() $p_k^N=(\widetilde {p}_k^N,u_{k-1}^N)$
. By induction, we have
$p_k^N=(\widetilde {p}_k^N,u_{k-1}^N)$
. By induction, we have
![]() $\widetilde {p}_k^C=q_k^C$
and
$\widetilde {p}_k^C=q_k^C$
and
![]() $\widetilde {p}_k^N=q_k^N$
, and since
$\widetilde {p}_k^N=q_k^N$
, and since
![]() $\pi (q_k^C)=q_k^N$
, we have
$\pi (q_k^C)=q_k^N$
, we have
![]() $\pi (\widetilde {p}_k^C)=\widetilde {p}_k^N$
. So we just need
$\pi (\widetilde {p}_k^C)=\widetilde {p}_k^N$
. So we just need
![]() $\pi (u_{k-1}^C)=u_{k-1}^N$
. For this, the only condition that remains to be verified is that
$\pi (u_{k-1}^C)=u_{k-1}^N$
. For this, the only condition that remains to be verified is that
![]() $\pi $
preserves
$\pi $
preserves
![]() $(k-1)$
-u-solidity witnesses. But this follows immediately from
$(k-1)$
-u-solidity witnesses. But this follows immediately from
![]() $\mathrm {r}\Sigma _{k+1}$
-elementarity (in fact
$\mathrm {r}\Sigma _{k+1}$
-elementarity (in fact
![]() $\mathrm {r}\Sigma _k$
-elementarity) together with preservation of the earlier defined objects (from the fine structural recursion). The (full)
$\mathrm {r}\Sigma _k$
-elementarity) together with preservation of the earlier defined objects (from the fine structural recursion). The (full)
![]() $\mathrm {r}\Sigma _{k+1}$
-elementarity of
$\mathrm {r}\Sigma _{k+1}$
-elementarity of
![]() $\pi $
and preservation of the
$\pi $
and preservation of the
![]() $q_i$
’s for
$q_i$
’s for
![]() $i\leq k$
similarly gives 3(iii), and part 3(iv) is likewise.
$i\leq k$
similarly gives 3(iii), and part 3(iv) is likewise.
Part 4 follows easily from part 3, according to which,
![]() $u_k^N$
is automatically in the relevant hulls.
$u_k^N$
is automatically in the relevant hulls.
Acknowledgements
The author acknowledges TU Wien Bibliothek for financial support through its Open Access Funding Programme. The author thanks John Steel for his hospitality during the author’s stay at UC Berkeley in 2012/13, and Steel’s NSF grant, for supporting the author during that stay, when the work in Section 5 was done. The author thanks the anonymous referee for their work and various corrections and suggestions for improvements. The author thanks the Institut für Mathematische Logik und Grundlagenforschung, Universität Münster, for the opportunity to present the inductive condensation stack argument in Section 3 at the Oberseminar für Mengenlehre in Spring 2016, and also the organizers of the 1st Irvine conference on descriptive inner model theory and hod mice (Irvine, July 2016) for the opportunity to present it at that conference.