Article contents
The deduction theorem in a functional calculus of first order based on strict implication
Published online by Cambridge University Press: 12 March 2014
Extract
In a previous paper, a functional calculus based on strict implication was developed. That system will be referred to as S2. The system resulting from the addition of Becker's axiom 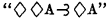 will be referred to as S4. In the present paper we will shw that a restricted deduction theorem is provable in S4 or more precisely in a system equivalent to S4. We will also show that such a deduction theorem is not provable in S2.
will be referred to as S4. In the present paper we will shw that a restricted deduction theorem is provable in S4 or more precisely in a system equivalent to S4. We will also show that such a deduction theorem is not provable in S2.
The following theorems not derived in Symbolic logic will be required for the fundamental theorems XXVIII* and XXIX* of this paper. We will state most of them without proofs.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1947
References
1 A functional calculus of first order based on strict implication, this Journal, vol. 11 (1946), pp. 1-16.
2 See Lewis, and Langford, , Symbolic logic, pp. 497–502.Google Scholar
3 Part of this paper was included in a dissertation written in partial fulfillment of the requirements for the Ph.D. degree in Philosophy at Yale University. I am grateful to Professor Frederic B. Fitch for his criticisms and suggestions.
4 Parry, W. T., The postulates for “strict implication,” Mind, vol. 43 (1934), pp. 78–80.CrossRefGoogle Scholar
5 This method for interpreting the quantifiers was suggested by the referee.
6
If Γ ![]() Ε is provable then (α1)(α2) … (αm)(Γ
Ε is provable then (α1)(α2) … (αm)(Γ ![]() Ε) is provable where α1 ,α2, … αm is a complete list of the free variables in Γ and Ε. We will assume that wherever B1 follows by substitution, the variables in Γ and Ε have been generalized upon.
Ε) is provable where α1 ,α2, … αm is a complete list of the free variables in Γ and Ε. We will assume that wherever B1 follows by substitution, the variables in Γ and Ε have been generalized upon.
7
A slightly stronger theorem than XXIX* could be proved as an immediate corollary of XXVIII* if we introduced the following lemma: If ├ A ⊃ B then ├ □ ⊃ □B We would then need only to assume that ├ An
![]() □Γ1 where i < n. This alternative proof was suggested by the referee.
□Γ1 where i < n. This alternative proof was suggested by the referee.
- 22
- Cited by


