Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T21:35:04.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of totally transcendental modules

Published online by Cambridge University Press:  12 March 2014

Steven Garavaglia
Steven Garavaglia*
Affiliation:
University of California at Berkeley, Berkeley, CA 94720
Get access Rights & Permissions [Opens in a new window]

Extract

The main theorem of this paper states that if R is a ring and 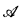is a totally transcendental R-module, then 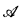has a unique decomposition as a direct sum of indecomposable R-modules. Natural examples of totally transcendental modules are injective modules over noetherian rings, artinian modules over commutative rings, projective modules over left-perfect, right-coherent rings, and arbitrary modules over Σ – α-gens rings. Therefore, our decomposition theorem yields as special cases the purely algebraic unique decomposition theorems for these four classes of modules due to Matlis; Warfield; Mueller, Eklof, and Sabbagh; and Shelah and Fisher. These results and a number of other corollaries about totally transcendental modules are covered in §1. In §2, I show how the results of § 1 can be used to give an improvement of Baur's classification of ω-categorical modules over countable rings. In §3, the decomposition theorem is used to study modules with quantifier elimination over noetherian rings.

The goals of this section are to prove the decomposition theorem and to derive some of its immediate corollaries. I will begin with some notational conventions. R will denote a ring with an identity element. LR is the language of left R-modules described in [4, p. 251] and TR is the theory of left R-modules. “R-module” will mean “unital left R-module”. A formula will mean an LR-formula.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 45 , Issue 1 , March 1980 , pp. 155 - 164
Copyright
Copyright © Association for Symbolic Logic 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

1.Azumaya, G., Corrections and supplementaries to my paper concerning Krull-Remak-Schmidt's theorem, Nagoya Mathematical Journal, vol. 1 (1950), pp. 117–124.CrossRefGoogle Scholar
2.Baur, W., ℵ-categorical modules, this Journal, vol. 40 (1975), pp. 213–219.Google Scholar
3.Baur, W., Elimination of quantifiers for modules, Israel Journal of Mathematics, vol. 25 (1976), pp. 64–70.CrossRefGoogle Scholar
4.Eklof, P. and Sabbagh, G., Model-completions and modules, Annals of Mathematical Logic, vol. 2 (1971), pp. 251–295.CrossRefGoogle Scholar
5.Eklof, P. and Sabbagh, G., Definability problems for modules and rings, this Journal, vol. 36 (1971), pp. 623–649.Google Scholar
6.Faith, C., Algebra II: Ring theory, Springer-Verlag, Berlin and New York, 1976.CrossRefGoogle Scholar
7.Fisher, E., Abelian structures, unpublished manuscript.Google Scholar
8.Garavaglia, S., Direct product decomposition of theories of modules, this Journal (to appear).Google Scholar
9.Kaplansky, I., Projective modules, Annals of Mathematics, vol. 68 (1958), pp. 372–377.CrossRefGoogle Scholar
10.Macintyre, A., On ω-categorical theories of abelian groups, Fundamenta Mathematicae, vol. 120 (1971), pp. 253–270.CrossRefGoogle Scholar
11.Matlis, E., Injective modules over noetherian rings, Pacific Journal of Mathematics, vol. 8 (1958), pp. 511–528.CrossRefGoogle Scholar
12.Monk, L., Elementary recursive decision procedures, Ph.D. dissertation, University of California, Berkeley, 1975.Google Scholar
13.Rosenstein, J., Theories which are not ℵ0-categorical, Proceedings of the School in Logic, Leeds, 1967, Lecture Notes in Mathematics, vol. 70, Springer-Verlag, Berlin and New York, 1968, pp. 273–278.Google Scholar
14.Sacks, G., Saturated model theory, W. A. Benjamin, Reading, Massachusetts, 1972.Google Scholar
15.Shelah, S., Uniqueness and characterization of prime models over sets for totally transcendental first-order theories, this Journal, vol. 37 (1972), pp. 107–113.Google Scholar
16.Shelah, S., The lazy model-theoretician's guide to stability, Proceedings of the Louvain Model Theory Conference, Logique et Analyse, vol. 71–72 (1975), pp. 242–308.Google Scholar
17.Warfield, R., A Krull-Schmidt theorem for infinite sums of modules, Proceedings of the American Mathematical Society, vol. 22 (1969), pp. 460–464.CrossRefGoogle Scholar