Published online by Cambridge University Press: 12 March 2014
This paper is a continuation of our previous work in [12]. The results, and some applications, have been described in the announcement [13]; it may be useful to discuss here, a little more fully, the nature and purpose of this work.
We are concerned basically with three kinds of algorithmic problem: (1) isomorphism problems, (2) “orbit problems”, and (3) “effective generation”.
(1) Isomorphism problems. Here we have a class 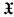 of algebraic objects of some kind, and ask: is there a uniform algorithm for deciding whether two arbitrary members of
of algebraic objects of some kind, and ask: is there a uniform algorithm for deciding whether two arbitrary members of 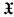 are isomorphic? In most cases, the answer is no: no such algorithm exists. Indeed this has been one of the most notable applications of methods of mathematical logic in algebra (see [26, Chapter IV, §4] for the case where
are isomorphic? In most cases, the answer is no: no such algorithm exists. Indeed this has been one of the most notable applications of methods of mathematical logic in algebra (see [26, Chapter IV, §4] for the case where 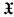 is the class of all finitely presented groups). It turns out, however, that when
is the class of all finitely presented groups). It turns out, however, that when 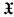 consists of objects which are in a certain sense “finite-dimensional”, then the isomorphism problem is indeed algorithmically soluble. We gave such algorithms in [12] for the following cases:
consists of objects which are in a certain sense “finite-dimensional”, then the isomorphism problem is indeed algorithmically soluble. We gave such algorithms in [12] for the following cases:
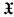 = {finitely generated nilpotent groups};
= {finitely generated nilpotent groups};
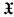 = {(not necessarily associative) rings whose additive group is finitely generated};
= {(not necessarily associative) rings whose additive group is finitely generated};
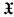 = {finitely Z-generated modules over a fixed finitely generated ring}.
= {finitely Z-generated modules over a fixed finitely generated ring}.
Combining the methods of [12] with his own earlier work, Sarkisian has obtained analogous results with the integers replaced by the rationals: in [20] and [21] he solves the isomorphism problem for radicable torsion-free nilpotent groups of finite rank and for finite-dimensional Q-algebras.