Article contents
DECIDABLE ALGEBRAIC FIELDS
Published online by Cambridge University Press: 19 June 2017
Abstract
We discuss the connection between decidability of a theory of a large algebraic extensions of 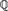 ${\Bbb Q}$ and the recursiveness of the field as a subset of a fixed algebraic closure. In particular, we prove that if an algebraic extension K of
${\Bbb Q}$ and the recursiveness of the field as a subset of a fixed algebraic closure. In particular, we prove that if an algebraic extension K of 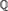 ${\Bbb Q}$ has a decidable existential theory, then within any fixed algebraic closure
${\Bbb Q}$ has a decidable existential theory, then within any fixed algebraic closure 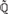 $\widetilde{\Bbb Q}$ of
$\widetilde{\Bbb Q}$ of 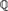 ${\Bbb Q}$, the field K must be conjugate over
${\Bbb Q}$, the field K must be conjugate over 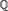 ${\Bbb Q}$ to a field which is recursive as a subset of the algebraic closure. We also show that for each positive integer e there are infinitely many e-tuples
${\Bbb Q}$ to a field which is recursive as a subset of the algebraic closure. We also show that for each positive integer e there are infinitely many e-tuples 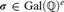 $\sigma \in {\text{Gal}}\left( {\Bbb Q} \right)^e $ such that the field
$\sigma \in {\text{Gal}}\left( {\Bbb Q} \right)^e $ such that the field 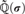 $\widetilde{\Bbb Q}\left( \sigma \right)$ is primitive recursive in
$\widetilde{\Bbb Q}\left( \sigma \right)$ is primitive recursive in 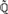 $\widetilde{\Bbb Q}$ and its elementary theory is primitive recursively decidable. Moreover,
$\widetilde{\Bbb Q}$ and its elementary theory is primitive recursively decidable. Moreover, 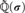 $\widetilde{\Bbb Q}\left( \sigma \right)$ is PAC and
$\widetilde{\Bbb Q}\left( \sigma \right)$ is PAC and 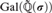 ${\text{Gal}}\left( {\widetilde{\Bbb Q}\left( \sigma \right)} \right)$ is isomorphic to the free profinite group on e generators.
${\text{Gal}}\left( {\widetilde{\Bbb Q}\left( \sigma \right)} \right)$ is isomorphic to the free profinite group on e generators.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 3
- Cited by


