Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Siefkes, Dirk
1971.
Undecidable Extensions of Monadic Second Order Successor Arithmetic.
Mathematical Logic Quarterly,
Vol. 17,
Issue. 1,
p.
385.
Thomas, Wolfgang
1975.
A note on undecidable extensions of monadic second order successor arithmetic.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 17,
Issue. 1-2,
p.
43.
Meyer, Albert R.
1975.
Logic Colloquium.
Vol. 453,
Issue. ,
p.
132.
Cohen, Rina S.
and
Gold, Arie Y.
1977.
Theory of ω-languagesI: Characterizations of ω-context-free languages.
Journal of Computer and System Sciences,
Vol. 15,
Issue. 2,
p.
169.
Thomas, Wolfgang
1978.
The theory of successor with an extra predicate.
Mathematische Annalen,
Vol. 237,
Issue. 2,
p.
121.
Choueka, Yaacov
1978.
Finite automata, definable sets, and regular expressions over ωn-tapes.
Journal of Computer and System Sciences,
Vol. 17,
Issue. 1,
p.
81.
Seese, Detlef G.
1978.
Über Unentscheidbare Erweiterungen von SC.
Mathematical Logic Quarterly,
Vol. 24,
Issue. 1-6,
p.
63.
Ono, Hiroakira
and
Nakamura, Akira
1979.
Undecidability of the first-order arithmetic A[P(x), 2x, x + 1].
Journal of Computer and System Sciences,
Vol. 18,
Issue. 3,
p.
243.
Ono, Hiroakira
and
Nakamura, Akira
1981.
Logic Symposia Hakone 1979, 1980.
Vol. 891,
Issue. ,
p.
155.
Lisovik, L. P.
1983.
Minimal undecidable identity problem for finite-automaton mappings.
Cybernetics,
Vol. 19,
Issue. 2,
p.
160.
Shepherdson, J.C.
1983.
Calvin C. Elgot 1922–1980.
Journal of Computer and System Sciences,
Vol. 27,
Issue. 2,
p.
141.
Semenov, A. L.
1984.
Mathematical Foundations of Computer Science 1984.
Vol. 176,
Issue. ,
p.
162.
Lisovik, L. P.
1984.
Construction of decidable singular theories of two successor functions with an extra predicate.
Algebra and Logic,
Vol. 23,
Issue. 3,
p.
181.
Muller, David E.
and
Schupp, Paul E.
1985.
The theory of ends, pushdown automata, and second-order logic.
Theoretical Computer Science,
Vol. 37,
Issue. ,
p.
51.
Gasarch, W.I.
1988.
Learning via queries.
p.
130.
THOMAS, Wolfgang
1990.
Formal Models and Semantics.
p.
133.
Thomas, Wolfgang
1990.
STACS 90.
Vol. 415,
Issue. ,
p.
263.
Thomas, Wolfgang
1991.
Automata, Languages and Programming.
Vol. 510,
Issue. ,
p.
441.
Thomas, Wolfgang
1992.
Infinite trees and automaton- definable relations over ω-words.
Theoretical Computer Science,
Vol. 103,
Issue. 1,
p.
143.
Villemaire, Roger
1992.
The theory of 〈N, +, Vk, Vl〉 is undecidable.
Theoretical Computer Science,
Vol. 106,
Issue. 2,
p.
337.
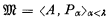 be a structure where A is a non-empty set, λ is an ordinal, and Pα is an n(α)-ary relation or function4 on A. With
be a structure where A is a non-empty set, λ is an ordinal, and Pα is an n(α)-ary relation or function4 on A. With 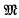 we associate a language L appropriate for
we associate a language L appropriate for 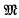 which may be a first or higher order calculus. L has an n(α)-place predicate or function constant P for each α < λ. We shall study three types of languages: (1) first-order calculi with equality; (2) second-order monadic calculi which contain monadic predicate (set) variables ranging over subsets of A; (3) restricted (weak) second-order calculi which contain monadic predicate variables ranging over finite subsets of A.
which may be a first or higher order calculus. L has an n(α)-place predicate or function constant P for each α < λ. We shall study three types of languages: (1) first-order calculi with equality; (2) second-order monadic calculi which contain monadic predicate (set) variables ranging over subsets of A; (3) restricted (weak) second-order calculi which contain monadic predicate variables ranging over finite subsets of A.

