Article contents
Decidability and ℵ0-categoricity of theories of partially ordered sets
Published online by Cambridge University Press: 12 March 2014
Abstract
This paper is primarily concerned with ℵ0-categoricity of theories of partially ordered sets. It contains some general conjectures, a collection of known results and some new theorems on ℵ0-categoricity. Among the latter are the following.
Corollary 3.3. For every countable ℵ0-categorical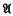 there is a linear order of A such that (
there is a linear order of A such that (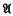 , <) is ℵ0-categorical.
, <) is ℵ0-categorical.
Corollary 6.7. Every ℵ0-categorical theory of a partially ordered set of finite width has a decidable theory.
Theorem 7.7. Every ℵ0-categorical theory of reticles has a decidable theory.
There is a section dealing just with decidability of partially ordered sets, the main result of this section being
Theorem 8.2. If (P, <) is a finite partially ordered set and KP is the class of partially ordered sets which do not embed (P, <), then Th(KP) is decidable iff KP contains only reticles.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1980
References
REFERENCES
- 11
- Cited by


