Article contents
Craig interpolation theorem for intuitionistic logic and extensions Part III
Published online by Cambridge University Press: 12 March 2014
Extract
This is a continuation of two previous papers by the same title [2] and examines mainly the interpolation property for the logic CD with constant domains, i.e., the extension of the intuitionistic predicate logic with the schema
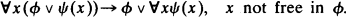
It is known [3], [4] that this logic is complete for the class of all Kripke structures with constant domains.
Theorem 47. The strong Robinson consistency theorem is not true for CD.
Proof. Consider the following Kripke structure with constant domains. The set S of possible worlds is ω0, the set of positive integers. R is the natural ordering ≤. Let ω0 0 = 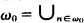 , Bn, is a sequence of pairwise disjoint infinite sets. Let L0 be a language with the unary predicates P, P1 and consider the
following extensions for P,P1 at the world m.
, Bn, is a sequence of pairwise disjoint infinite sets. Let L0 be a language with the unary predicates P, P1 and consider the
following extensions for P,P1 at the world m.
(a) P is true on ⋃i≤2nBi, and P1 is true on ⋃i≤2n+1Bi for m = 2n.
(b) P is true on ⋃i≤2nBi, and P1 for ⋃i≤2n+1Bi for m = 2n.
Let (Δ,Θ) be the complete theory of this structure. Consider another unary predicate Q. Let L be the language with P, Q and let M be the language with P1, Q.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1977
References
REFERENCES
- 5
- Cited by


