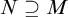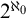1 Introduction
The model-theoretic condition of cellularity has appeared several times as a dividing line in the complexity of universal theories, including when counting the number of countable models [Reference Macpherson, Pouzet and Woodrow14], counting the number of finite models as a function of size [Reference Laskowski and Terry12], and counting the number of non-isomorphic substructures of countable models [Reference Laskowski and Mayer11]. In this paper, we present a general approach to proving results about cellularity via another model-theoretic condition, mutual algebraicity. The approach is to first prove that the non-mutually algebraic case is wild, likely using the Ryll–Nardzewski-type characterization of mutual algebraicity from [Reference Laskowski and Terry13]. In a companion paper [Reference Braunfeld and Laskowski3], we characterize the mutually algebraic non-cellular case. As mutually algebraic structures admit a nice structural decomposition, it is relatively quick to prove the mutually algebraic non-cellular case is still wild. This approach was already largely present in [Reference Laskowski and Terry12], and we apply it here to the question of counting siblings.
We call two (not necessarily elementarily) bi-embeddable structures siblings (
![]() $f \colon M \hookrightarrow N$
is an embedding if
$f \colon M \hookrightarrow N$
is an embedding if
![]() $R(x_1, \dots , x_n) \iff R(f(x_1), \dots , f(x_n))$
for every atomic relation R). Given a countable relational structure M, our goal is to count the number of siblings of M, up to isomorphism. Thomassé has conjectured the following, counting M as a sibling of itself.
$R(x_1, \dots , x_n) \iff R(f(x_1), \dots , f(x_n))$
for every atomic relation R). Given a countable relational structure M, our goal is to count the number of siblings of M, up to isomorphism. Thomassé has conjectured the following, counting M as a sibling of itself.
Conjecture 1 (Thomassé [Reference Thomassé16]).
Given a countable structure M in a countable relational language, M has either 1,
![]() ${\aleph _0}$
, or
${\aleph _0}$
, or
![]() $2^{\aleph _0}$
siblings, up to isomorphism.
$2^{\aleph _0}$
siblings, up to isomorphism.
This conjecture has been proven in the case of linear orders [Reference Laflamme, Pouzet and Woodrow8], the gap from 1 to
![]() ${\aleph _0}$
proven for
${\aleph _0}$
proven for
![]() ${\aleph _0}$
-categorical structures by making use of the monomorphic decomposition [Reference Laflamme, Pouzet, Sauer and Woodrow7], and the gap from 1 to
${\aleph _0}$
-categorical structures by making use of the monomorphic decomposition [Reference Laflamme, Pouzet, Sauer and Woodrow7], and the gap from 1 to
![]() ${\aleph _0}$
proven for cographs [Reference Hahn, Pouzet and Woodrow5]. The gap from 1 to
${\aleph _0}$
proven for cographs [Reference Hahn, Pouzet and Woodrow5]. The gap from 1 to
![]() ${\aleph _0}$
has also been conjectured in the case of graphs, connected graphs where the siblings must also be connected [Reference Bonato, Bruhn, Diestel and Sprüssel1], and trees where the siblings must also be trees (as opposed to forests) [Reference Bonato and Tardif2], and some partial results obtained in these cases.
${\aleph _0}$
has also been conjectured in the case of graphs, connected graphs where the siblings must also be connected [Reference Bonato, Bruhn, Diestel and Sprüssel1], and trees where the siblings must also be trees (as opposed to forests) [Reference Bonato and Tardif2], and some partial results obtained in these cases.
If two structures are siblings, they must have the same finite substructures, and so satisfy the same universal theory. Thus, we may coarsen Thomassé’s conjecture to considering the maximum number of siblings of any model of a given universal theory, which may be viewed as a measure of complexity of that theory. Indeed, for a model to have many siblings, we must produce non-isomorphic structures that look somewhat alike (the similarity required for siblings may be increased by requiring elementary bi-embeddability, as in [Reference Goodrick4]). Complex theories will allow their models to be nuanced enough to admit many siblings. Uncomplicated theories will not allow for such nuance, and so whenever models look alike, they will be the same (for example, the theory of n disjoint unary predicates, where models are isomorphic once the cardinalities of the predicates match). The complexity gaps of Thomassé’s conjecture then call to mind model-theoretic dividing lines.
However, we note that it is possible for individual structures to be very complicated, yet have few siblings. For example,
![]() $\omega $
with successor has only itself as a sibling. Thus the same is true of any expansion, in particular the expansion by the graphs of addition and multiplication. So it is difficult to see how model theory will inform the full conjecture.
$\omega $
with successor has only itself as a sibling. Thus the same is true of any expansion, in particular the expansion by the graphs of addition and multiplication. So it is difficult to see how model theory will inform the full conjecture.
Our main theorem confirms the weakening of Thomassé’s conjecture to the level of universal theories in a finite relational language.
Theorem 1.1 (Theorem 7.11).
Let T be a universal theory in a finite relational language. Then one of the following holds.
-
1. T is finitely partitioned. Every model of T has one sibling.
-
2. T is cellular. The finitely partitioned models of T have one sibling and the non-finitely partitioned models have
 $\aleph _0$
siblings.
$\aleph _0$
siblings. -
3. T is not cellular. For every non-cellular
 $M \models T$
, there is some
$M \models T$
, there is some
 $N \supseteq M$
such that
$N \supseteq M$
such that
 $N \models T$
and N has
$N \models T$
and N has
 $2^{\aleph _0}$
siblings. Furthermore, if T is mutually algebraic, we may take
$2^{\aleph _0}$
siblings. Furthermore, if T is mutually algebraic, we may take
 $N \succeq M$
.
$N \succeq M$
.
Theorem 1.1 does have implications at the level of structures, confirming some conjectures of [Reference Laflamme, Pouzet, Sauer and Woodrow7].
Corollary 1.2 (Corollary 7.12).
Let M be a countable model in a finite relational language that is universal for its age. Then one of the following holds.
-
1. M is finitely partitioned, and has one sibling.
-
2. M is cellular but not finitely partitioned, and has
 $\aleph _0$
siblings.
$\aleph _0$
siblings. -
3. M is not cellular, and has
 $2^{\aleph _0}$
siblings.
$2^{\aleph _0}$
siblings.
This also implies the result for
![]() $\omega $
-categorical M in a finite relational language, since then we may pass to its model companion. Example 6 shows Corollary 1.2 does not hold for infinite relational languages with finite profile.
$\omega $
-categorical M in a finite relational language, since then we may pass to its model companion. Example 6 shows Corollary 1.2 does not hold for infinite relational languages with finite profile.
We close with some comments connecting our results to previous work on cellularity. First, we note that Theorem 1.1 is a refinement of the main result of [Reference Macpherson, Pouzet and Woodrow14] that non-cellular universal theories have
![]() $2^{\aleph _0}$
non-isomorphic models. Second, Corollary 1.2 may be seen as a dual to the main result of [Reference Laskowski and Mayer11] that an atomically stable non-cellular countable structure has
$2^{\aleph _0}$
non-isomorphic models. Second, Corollary 1.2 may be seen as a dual to the main result of [Reference Laskowski and Mayer11] that an atomically stable non-cellular countable structure has
![]() $2^{\aleph _0}$
non-isomorphic substructures. When M is universal for its age, as in Corollary 1.2, siblings are equivalent to age-preserving extensions, and we again see cellularity is the dividing line between
$2^{\aleph _0}$
non-isomorphic substructures. When M is universal for its age, as in Corollary 1.2, siblings are equivalent to age-preserving extensions, and we again see cellularity is the dividing line between
![]() ${\aleph _0}$
and
${\aleph _0}$
and
![]() $2^{\aleph _0}$
.
$2^{\aleph _0}$
.
1.1 Proof sketch
The primary intuition behind the proof of the main theorem is that if a universal theory T is non-cellular, then either it is unstable and so has a model encoding
![]() $(\mathbb {Q}, <)$
, or has a model that in some sense encodes a partition with infinitely many infinite parts. We present three examples corresponding to the three cases of our proof, and explain how to obtain
$(\mathbb {Q}, <)$
, or has a model that in some sense encodes a partition with infinitely many infinite parts. We present three examples corresponding to the three cases of our proof, and explain how to obtain
![]() $2^{\aleph _0}$
many siblings in each.
$2^{\aleph _0}$
many siblings in each.
-
1. Let
 $M = (\mathbb {Q}, \leq )$
. Then any countable non-scattered order is a sibling of M, and there are
$M = (\mathbb {Q}, \leq )$
. Then any countable non-scattered order is a sibling of M, and there are
 $2^{\aleph _0}$
many.
$2^{\aleph _0}$
many. -
2. Let M be an equivalence relation with infinitely many infinite classes. Then we may pass to an elementary extension
 $M^* \succ M$
containing infinitely many new infinite classes
$M^* \succ M$
containing infinitely many new infinite classes
 . For each injective
. For each injective
 $f\colon \mathbb {Q} \to \omega $
, let
$f\colon \mathbb {Q} \to \omega $
, let
 $M_f$
be obtained by cutting down each
$M_f$
be obtained by cutting down each
 ${\mathcal A}_q$
to size
${\mathcal A}_q$
to size
 $f(q)$
. Then each
$f(q)$
. Then each
 $M_f$
is a sibling of M, and they are pairwise non-isomorphic, as they have distinct sizes of finite classes.
$M_f$
is a sibling of M, and they are pairwise non-isomorphic, as they have distinct sizes of finite classes. -
3. Let
 $M = (\omega , s)$
, where s is the successor relation. We first pass to an elementary extension
$M = (\omega , s)$
, where s is the successor relation. We first pass to an elementary extension
 $M' \succ M$
containing infinitely many
$M' \succ M$
containing infinitely many
 $\mathbb {Z}$
-chains. Then, as in case (2), we may pass to a further elementary extension
$\mathbb {Z}$
-chains. Then, as in case (2), we may pass to a further elementary extension
 $M^* \succ M'$
containing infinitely many new
$M^* \succ M'$
containing infinitely many new
 $\mathbb {Z}$
-chains
$\mathbb {Z}$
-chains
 . For each injective
. For each injective
 $f\colon \mathbb {Q} \to \omega $
, we let
$f\colon \mathbb {Q} \to \omega $
, we let
 $M_f$
be obtained by cutting down each
$M_f$
be obtained by cutting down each
 ${\mathcal A}_q$
to a connected piece of size
${\mathcal A}_q$
to a connected piece of size
 $f(q)$
.
$f(q)$
.
Our proof follows these three examples. The bulk of the work is in generalizing Case 2 to the setting of a non-mutually algebraic M. The role played by equivalence classes is generalized to that of k-cliques in Section 4, while Section 3 guarantees that if we cannot add such k-cliques to M, then we may find many siblings as in Case 1. Otherwise, for M non-mutually algebraic, we may generalize the proof of Case 2 by adding infinitely many k-cliques to M, which is done in Sections 5 and 6. Finally, for M mutually algebraic but non-cellular, we generalize Case 3 in Section 7.
2 Conventions and background
The following conventions will be in effect throughout this paper, unless otherwise noted.
M is a countable structure in a finite relational language
![]() ${\mathcal L}$
.
${\mathcal L}$
.
Types are quantifier-free types, and indiscernibility is with respect to quantifier-free formulas.
We now briefly cover the definitions and results from elsewhere that we will need.
Definition 2.1. A structure M is finitely partitioned if it admits a finite partition
![]() such that
such that
![]() $\Pi _i Sym(C_i) \subset Aut(M)$
.
$\Pi _i Sym(C_i) \subset Aut(M)$
.
Definition 2.2. A structure M is cellular if, for some n and
![]() $k_1, \dots , k_n \in \omega $
, it admits a partition
$k_1, \dots , k_n \in \omega $
, it admits a partition
![]() satisfying the following.
satisfying the following.
-
1. K is finite, and each
 $\bar {c}_{i,j}=(c_{i,j}^1,\dots , c_{i,j}^{k_i})$
has length
$\bar {c}_{i,j}=(c_{i,j}^1,\dots , c_{i,j}^{k_i})$
has length
 $k_i$
.
$k_i$
. -
2. For every
 $i \in [n]$
and
$i \in [n]$
and
 $\sigma \in S_\infty $
, there is a
$\sigma \in S_\infty $
, there is a
 $\sigma _i^* \in Aut(M)$
mapping each
$\sigma _i^* \in Aut(M)$
mapping each
 $\bar {c}_{i,j}$
onto
$\bar {c}_{i,j}$
onto
 $\bar {c}_{i, \sigma (j)}$
by sending
$\bar {c}_{i, \sigma (j)}$
by sending
 $c_{i,j}^\ell $
to
$c_{i,j}^\ell $
to
 $c_{i, \sigma (j)}^\ell $
for
$c_{i, \sigma (j)}^\ell $
for
 $1 \leq \ell \leq {k_i}$
, and fixing
$1 \leq \ell \leq {k_i}$
, and fixing
 $M \backslash \bigcup _{j \in \omega } \bar {c}_{i, j}$
pointwise.
$M \backslash \bigcup _{j \in \omega } \bar {c}_{i, j}$
pointwise.
We call such a partition a cellular partition.
Example 1. Let M be a graph consisting of infinitely many disjoint edges and an infinite clique. Then M is cellular—we may take
![]() $K = \emptyset $
and
$K = \emptyset $
and
![]() $n=2$
, let
$n=2$
, let
![]() enumerate the disjoint edges, and let
enumerate the disjoint edges, and let
![]() enumerate the clique.
enumerate the clique.
Note M is finitely partitioned if and only if M is cellular as witnessed by a partition with each
![]() $k_i=1$
. The following definitions are from [Reference Laskowski10], which builds on results from [Reference Laskowski9].
$k_i=1$
. The following definitions are from [Reference Laskowski10], which builds on results from [Reference Laskowski9].
Definition 2.3. Given a structure M and
![]() $n\ge 1$
, a set
$n\ge 1$
, a set
![]() $S\subseteq M^n$
is mutually algebraic if there is some
$S\subseteq M^n$
is mutually algebraic if there is some
![]() $K\in \omega $
such that
$K\in \omega $
such that
![]() $|\{\bar {a}\in S:m\in \bar {a}\}|\le K$
for every
$|\{\bar {a}\in S:m\in \bar {a}\}|\le K$
for every
![]() $m\in M$
. Let
$m\in M$
. Let
![]() ${\mathcal L}_M$
be
${\mathcal L}_M$
be
![]() ${\mathcal L}$
expanded by constant symbols for every element of M, and
${\mathcal L}$
expanded by constant symbols for every element of M, and
![]() $M_M$
the natural expansion of M to
$M_M$
the natural expansion of M to
![]() ${\mathcal L}_M$
. An
${\mathcal L}_M$
. An
![]() ${\mathcal L}_M$
-formula
${\mathcal L}_M$
-formula
![]() $\phi (x_1,\dots ,x_n)$
is mutually algebraic if it defines a mutually algebraic subset of
$\phi (x_1,\dots ,x_n)$
is mutually algebraic if it defines a mutually algebraic subset of
![]() $ M^n$
. We then let
$ M^n$
. We then let
![]() ${\mathcal M}{\mathcal A}^*(M)$
be the smallest set of
${\mathcal M}{\mathcal A}^*(M)$
be the smallest set of
![]() ${\mathcal L}_M$
-formulas containing the mutually algebraics, closed under adjunction of dummy variables and Boolean combinations.
${\mathcal L}_M$
-formulas containing the mutually algebraics, closed under adjunction of dummy variables and Boolean combinations.
Finally, we say M is mutually algebraic if every
![]() ${\mathcal L}_M$
-formula is equivalent to a formula in
${\mathcal L}_M$
-formula is equivalent to a formula in
![]() ${\mathcal M}{\mathcal A}^*(M)$
.
${\mathcal M}{\mathcal A}^*(M)$
.
Note that every unary relation is mutually algebraic. Less obviously, cellular structures are mutually algebraic.
Lemma 2.4. Let M be mutually algebraic and
![]() $N \subset M$
a substructure. Then N is mutually algebraic.
$N \subset M$
a substructure. Then N is mutually algebraic.
Proof. Let
![]() $(M,N)$
be the expansion of M formed by adding a unary predicate U interpreted as N. Let
$(M,N)$
be the expansion of M formed by adding a unary predicate U interpreted as N. Let
![]() ${N^{{\textrm {ind}}}}$
denote the expansion of N by relations
${N^{{\textrm {ind}}}}$
denote the expansion of N by relations
![]() $P_D$
naming the trace
$P_D$
naming the trace
![]() $D\cap N^n$
of every
$D\cap N^n$
of every
![]() $(M,N)$
-definable (with parameters) subset
$(M,N)$
-definable (with parameters) subset
![]() $D\subseteq M^n$
, for all n. As the set N is definable in
$D\subseteq M^n$
, for all n. As the set N is definable in
![]() $(M,N)$
, it is easily checked that
$(M,N)$
, it is easily checked that
![]() ${N^{{\textrm {ind}}}}$
admits elimination of quantifiers. Moreover, every parameter-definable set of
${N^{{\textrm {ind}}}}$
admits elimination of quantifiers. Moreover, every parameter-definable set of
![]() ${N^{{\textrm {ind}}}}$
is 0-definable in
${N^{{\textrm {ind}}}}$
is 0-definable in
![]() ${N^{{\textrm {ind}}}}$
, and is definable in
${N^{{\textrm {ind}}}}$
, and is definable in
![]() $(M,N)$
.
$(M,N)$
.
Claim.
![]() ${N^{{\textrm {ind}}}}$
is mutually algebraic.
${N^{{\textrm {ind}}}}$
is mutually algebraic.
Proof of Claim. We show that every
![]() ${N^{{\textrm {ind}}}}$
-definable subset
${N^{{\textrm {ind}}}}$
-definable subset
![]() $B\subseteq N^n$
is in
$B\subseteq N^n$
is in
![]() ${\mathcal M}{\mathcal A}^*({N^{{\textrm {ind}}}})$
. Since mutual algebraicity is preserved under unary expansions by Theorem 3.3 of [Reference Laskowski10],
${\mathcal M}{\mathcal A}^*({N^{{\textrm {ind}}}})$
. Since mutual algebraicity is preserved under unary expansions by Theorem 3.3 of [Reference Laskowski10],
![]() $(M,N)$
is mutually algebraic, and so B is in
$(M,N)$
is mutually algebraic, and so B is in
![]() ${\mathcal M}{\mathcal A}^*((M, N))$
, as witnessed by a Boolean combination of sets
${\mathcal M}{\mathcal A}^*((M, N))$
, as witnessed by a Boolean combination of sets
![]() , each realizing an adjunction of a mutually algebraic formula by dummy variables. As the same is true for each
, each realizing an adjunction of a mutually algebraic formula by dummy variables. As the same is true for each
![]() $Y_i\cap N^n$
,
$Y_i\cap N^n$
,
![]() $B\in {\mathcal M}{\mathcal A}^*({N^{{\textrm {ind}}}})$
.◊
$B\in {\mathcal M}{\mathcal A}^*({N^{{\textrm {ind}}}})$
.◊
It is easily checked that the L-structure N is a reduct of
![]() ${N^{{\textrm {ind}}}}$
; hence N is mutually algebraic by Corollary 7.4 of [Reference Laskowski and Terry13].⊣
${N^{{\textrm {ind}}}}$
; hence N is mutually algebraic by Corollary 7.4 of [Reference Laskowski and Terry13].⊣
In addition to mutual algebraicity, the properties of being finitely partitioned and cellular are preserved under passing to a substructure. Thus, they are properties of a universal theory, and so we will say a universal theory T has one of these properties if all of its countable models do.
We record one additional characterization of mutual algebraicity.
Theorem 2.5. [Reference Laskowski and Terry13, Theorem 2.1] M is mutually algebraic if and only if every atomic
![]() ${\mathcal L}$
-formula is
${\mathcal L}$
-formula is
![]() $Th(M_M)$
-equivalent to a Boolean combination of quantifier-free mutually algebraic
$Th(M_M)$
-equivalent to a Boolean combination of quantifier-free mutually algebraic
![]() ${\mathcal L}_M$
-formulas.
${\mathcal L}_M$
-formulas.
Example 2. Consider a structure
![]() $(M, E)$
where E is an equivalence relation with n classes, each class infinite. Then the relation E is not mutually algebraic. However, using the constants
$(M, E)$
where E is an equivalence relation with n classes, each class infinite. Then the relation E is not mutually algebraic. However, using the constants
![]() $m_1, \dots , m_n$
to name one element from each class, we have
$m_1, \dots , m_n$
to name one element from each class, we have
![]() $E(x, y) \iff \bigvee _i(E(x,m_i) \wedge E(y,m_i))$
, which is a Boolean combination of quantifier-free mutually algebraic
$E(x, y) \iff \bigvee _i(E(x,m_i) \wedge E(y,m_i))$
, which is a Boolean combination of quantifier-free mutually algebraic
![]() ${\mathcal L}_M$
-formulas. Thus M is mutually algebraic.
${\mathcal L}_M$
-formulas. Thus M is mutually algebraic.
Definition 2.6. Given a set A, let
![]() $\mathrm {QF}_k(A)$
be the set of quantifier-free formulas over A with k variables.
$\mathrm {QF}_k(A)$
be the set of quantifier-free formulas over A with k variables.
Given a structure M,
![]() $\bar {c} \in M^k$
, and
$\bar {c} \in M^k$
, and
![]() $A \subset M$
, the type of
$A \subset M$
, the type of
![]() $\bar {c}$
over A is
$\bar {c}$
over A is
![]() $\mathrm {tp}(\bar {c}/A) = \{\theta (\bar {x}) \in \mathrm {QF}_k(A) : M \models \theta (\bar {c})\}$
.
$\mathrm {tp}(\bar {c}/A) = \{\theta (\bar {x}) \in \mathrm {QF}_k(A) : M \models \theta (\bar {c})\}$
.
Given a structure M, a k-type over M is some
![]() $p(\bar {x}) \subset \mathrm {QF}_k(M)$
such that there is some elementary extension
$p(\bar {x}) \subset \mathrm {QF}_k(M)$
such that there is some elementary extension
![]() $N \succ M$
and
$N \succ M$
and
![]() $\bar {n} \in N^k$
such that
$\bar {n} \in N^k$
such that
![]() $p(\bar {x}) = \mathrm {tp}(\bar {n}/M)$
.
$p(\bar {x}) = \mathrm {tp}(\bar {n}/M)$
.
Definition 2.7. Given a structure M and a k-type p over M, we say p supports an infinite array if there is some
![]() $N \succ M$
and a set of pairwise disjoint k-tuples
$N \succ M$
and a set of pairwise disjoint k-tuples
![]() such that
such that
![]() $\bar {n}_i \models p$
, for every i.
$\bar {n}_i \models p$
, for every i.
We let
![]() $\mathrm {Supp}_k(M)$
denote the set of k-types over M that support infinite arrays.
$\mathrm {Supp}_k(M)$
denote the set of k-types over M that support infinite arrays.
We say
![]() $p(\bar {x})$
is coordinate-wise non-algebraic if
$p(\bar {x})$
is coordinate-wise non-algebraic if
![]() $(x_i\neq b)\in p$
for every
$(x_i\neq b)\in p$
for every
![]() $x_i\in \bar {x}$
and every
$x_i\in \bar {x}$
and every
![]() $b\in M$
.
$b\in M$
.
Lemma 2.8. Let M be any structure, and
![]() $p(\bar {x})$
a type over M. Then
$p(\bar {x})$
a type over M. Then
![]() $p \in \mathrm {Supp}_k(M)$
if and only if
$p \in \mathrm {Supp}_k(M)$
if and only if
![]() $p(\bar {x})$
is coordinate-wise non-algebraic.
$p(\bar {x})$
is coordinate-wise non-algebraic.
Proof. If
![]() $(x_i=b)\in p$
for some
$(x_i=b)\in p$
for some
![]() $x_i$
and some
$x_i$
and some
![]() $b\in M$
, then any two realizations of p have non-empty intersection, so p does not support an infinite array (or an array of length 2, for that matter). Conversely, assume p is coordinate-wise non-algebraic, but p does not support an infinite array. By compactness, there is some n and some
$b\in M$
, then any two realizations of p have non-empty intersection, so p does not support an infinite array (or an array of length 2, for that matter). Conversely, assume p is coordinate-wise non-algebraic, but p does not support an infinite array. By compactness, there is some n and some
![]() $\theta (\bar {x})\in p$
such that in M, there do not exist n pairwise disjoint realizations of
$\theta (\bar {x})\in p$
such that in M, there do not exist n pairwise disjoint realizations of
![]() $\theta $
. Among all such, choose
$\theta $
. Among all such, choose
![]() $\theta $
so that n is minimized, and choose
$\theta $
so that n is minimized, and choose
![]() from M, pairwise disjoint with
from M, pairwise disjoint with
![]() $M\models \theta (\bar {b}_i)$
for each i. Choose
$M\models \theta (\bar {b}_i)$
for each i. Choose
![]() $M^*\succeq M$
and
$M^*\succeq M$
and
![]() $\bar {a}$
from
$\bar {a}$
from
![]() $M^*$
realizing p. As p is coordinate-wise non-algebraic,
$M^*$
realizing p. As p is coordinate-wise non-algebraic,
![]() $\bar {a}$
is disjoint from M, hence disjoint from each
$\bar {a}$
is disjoint from M, hence disjoint from each
![]() $\bar {b}_i$
. Thus
$\bar {b}_i$
. Thus
![]() gives
gives
![]() $(n+1)$
pairwise disjoint realizations of
$(n+1)$
pairwise disjoint realizations of
![]() $\theta (\bar {x})$
, which is impossible since
$\theta (\bar {x})$
, which is impossible since
![]() $M^*\succeq M$
.⊣
$M^*\succeq M$
.⊣
Theorem 2.9. If M is not mutually algebraic, then there is some
![]() $M' \succ M$
and some
$M' \succ M$
and some
![]() $k \in \omega $
such that
$k \in \omega $
such that
![]() $\mathrm {Supp}_k(M')$
is infinite.
$\mathrm {Supp}_k(M')$
is infinite.
Proof. By [Reference Laskowski and Terry13, Theorem 6.1], there is some countable
![]() $M^* \equiv M$
and some k such that
$M^* \equiv M$
and some k such that
![]() $\mathrm {Supp}_k(M^*)$
is infinite. Let
$\mathrm {Supp}_k(M^*)$
is infinite. Let
![]() $M'$
elementarily embed M and
$M'$
elementarily embed M and
![]() $M^*$
. By compactness, every
$M^*$
. By compactness, every
![]() $p \in \mathrm {Supp}_k(M^*)$
extends to some
$p \in \mathrm {Supp}_k(M^*)$
extends to some
![]() $p' \in \mathrm {Supp}_k(M')$
.⊣
$p' \in \mathrm {Supp}_k(M')$
.⊣
Definition 2.10. Fix a structure M, let
![]() $S = (\bar {b}_i \in M^k : i \in (I, <))$
be a sequence of k-tuples, and let
$S = (\bar {b}_i \in M^k : i \in (I, <))$
be a sequence of k-tuples, and let
![]() $A \subset M$
. S is order indiscernible over A if
$A \subset M$
. S is order indiscernible over A if
![]() $\mathrm {tp}(\bar {b}_{i_1}, \dots , \bar {b}_{i_n}/A) = \mathrm {tp}(\bar {b}_{j_1}, \dots , \bar {b}_{j_n}/A)$
whenever
$\mathrm {tp}(\bar {b}_{i_1}, \dots , \bar {b}_{i_n}/A) = \mathrm {tp}(\bar {b}_{j_1}, \dots , \bar {b}_{j_n}/A)$
whenever
![]() $i_1 < \dots < i_n$
and
$i_1 < \dots < i_n$
and
![]() $j_1 < \dots < j_n$
(where, by our convention,
$j_1 < \dots < j_n$
(where, by our convention,
![]() $\mathrm {tp}$
is understood to mean quantifier-free type).
$\mathrm {tp}$
is understood to mean quantifier-free type).
S is totally indiscernible over A if
![]() $\mathrm {tp}(\bar {b}_{i_1}, \dots , \bar {b}_{i_n}/A) = \mathrm {tp}(\bar {b}_{j_1}, \dots , \bar {b}_{j_n}/A)$
whenever
$\mathrm {tp}(\bar {b}_{i_1}, \dots , \bar {b}_{i_n}/A) = \mathrm {tp}(\bar {b}_{j_1}, \dots , \bar {b}_{j_n}/A)$
whenever
![]() $i_1, \dots , i_n$
are pairwise distinct, as are
$i_1, \dots , i_n$
are pairwise distinct, as are
![]() $j_1, \dots j_n$
.
$j_1, \dots j_n$
.
S is strictly order indiscernible over A if it is order indiscernible over A but not totally indiscernible over A.
Definition 2.11. A countable structure M is universal for its age if every other countable structure with the same age embeds into M. Equivalently, M is countable universal for its universal theory.
3 Strictly order indiscernible arrays
As we are aiming to prove that cellularity is the dividing line between having a model with
![]() ${\aleph _0}$
and
${\aleph _0}$
and
![]() $2^{\aleph _0}$
siblings, we expect non-stability, as manifested by an infinite strictly order-indiscernible sequence of k-tuples, to provide a model with
$2^{\aleph _0}$
siblings, we expect non-stability, as manifested by an infinite strictly order-indiscernible sequence of k-tuples, to provide a model with
![]() $2^{\aleph _0}$
siblings. We prove this in the case of infinite arrays, but first we need a definition and easy lemma.
$2^{\aleph _0}$
siblings. We prove this in the case of infinite arrays, but first we need a definition and easy lemma.
Definition 3.1. For M non-mutually algebraic, M is array-minimal of index k if
![]() $\mathrm {Supp}_k(M)$
is infinite and there does not exist a
$\mathrm {Supp}_k(M)$
is infinite and there does not exist a
![]() $k'<k$
and an age-preserving
$k'<k$
and an age-preserving
![]() $N\supseteq M$
for which
$N\supseteq M$
for which
![]() $\mathrm {Supp}_{k'}(N)$
is infinite.
$\mathrm {Supp}_{k'}(N)$
is infinite.
Example 3. Consider the structure
![]() , where E is a binary relation such that
, where E is a binary relation such that
![]() $(q,i)E(r,j)$
iff
$(q,i)E(r,j)$
iff
![]() $q=r$
and
$q=r$
and
![]() $i \neq j$
, and
$i \neq j$
, and
![]() $\prec $
is a quaternary relation encoding the usual
$\prec $
is a quaternary relation encoding the usual
![]() $\leq $
relation between pairs of E-connected points. Then there is only one coordinate-wise non-algebraic 1-type over M, namely the type of an isolated point. The same will be true for any age-preserving
$\leq $
relation between pairs of E-connected points. Then there is only one coordinate-wise non-algebraic 1-type over M, namely the type of an isolated point. The same will be true for any age-preserving
![]() $N \supseteq M$
. However, there are infinitely many coordinate-wise non-algebraic 2-types over M—into any cut of M, we may insert an E-related pair of points. Thus M is array-minimal of index 2.
$N \supseteq M$
. However, there are infinitely many coordinate-wise non-algebraic 2-types over M—into any cut of M, we may insert an E-related pair of points. Thus M is array-minimal of index 2.
Lemma 3.2. If M is not mutually algebraic, then for some
![]() $k\ge 1$
, there is an age-preserving
$k\ge 1$
, there is an age-preserving
![]() $M'\supseteq M$
that is array-minimal of index k. Moreover, for every elementary extension
$M'\supseteq M$
that is array-minimal of index k. Moreover, for every elementary extension
![]() $M^*\succeq M'$
and for any substructure N with
$M^*\succeq M'$
and for any substructure N with
![]() $M'\subseteq N\subseteq M^*$
, N is also array-minimal of index k.
$M'\subseteq N\subseteq M^*$
, N is also array-minimal of index k.
Proof. As M is not mutually algebraic, by Theorem 2.9 there is some age-preserving
![]() $N \supseteq M$
and some
$N \supseteq M$
and some
![]() $\ell \in \omega $
such that
$\ell \in \omega $
such that
![]() $\mathrm {Supp}_\ell (N)$
is infinite. Among all age-preserving extensions of M, there is one with the least k such the extension has infinitely many k-types that support infinite arrays, and choose that extension to be
$\mathrm {Supp}_\ell (N)$
is infinite. Among all age-preserving extensions of M, there is one with the least k such the extension has infinitely many k-types that support infinite arrays, and choose that extension to be
![]() $M'$
.
$M'$
.
For the moreover clause, choose any
![]() $M'\subseteq N\subseteq M^*$
with
$M'\subseteq N\subseteq M^*$
with
![]() $M^*\succeq M'$
. Every
$M^*\succeq M'$
. Every
![]() $p\in \mathrm {Supp}_k(M')$
has an extension
$p\in \mathrm {Supp}_k(M')$
has an extension
![]() $p^*\in \mathrm {Supp}_k(M^*)$
. As the restriction of each of these types
$p^*\in \mathrm {Supp}_k(M^*)$
. As the restriction of each of these types
![]() $p^*$
to a type over N also supports an infinite array, N is also array-minimal of index k.⊣
$p^*$
to a type over N also supports an infinite array, N is also array-minimal of index k.⊣
Proposition 3.3. Suppose M is not mutually algebraic, M is array-minimal of index k, and that some
![]() $p\in \mathrm {Supp}_k(M)$
supports an infinite array
$p\in \mathrm {Supp}_k(M)$
supports an infinite array
![]() that is strictly order indiscernible over M. Then there is an age-preserving
that is strictly order indiscernible over M. Then there is an age-preserving
![]() $N\supseteq M$
with
$N\supseteq M$
with
![]() $2^{\aleph _0}$
siblings.
$2^{\aleph _0}$
siblings.
Proof. From our assumption on p and compactness, choose an elementary extension
![]() $M^*\succeq M$
containing a strictly order-indiscernible array
$M^*\succeq M$
containing a strictly order-indiscernible array
![]() of realizations of p. Let N be the substructure of
of realizations of p. Let N be the substructure of
![]() $M^*$
with universe
$M^*$
with universe
![]() $M\cup A$
, and let
$M\cup A$
, and let
![]() . Choose a family
. Choose a family
![]() of subsets of
of subsets of
![]() $(0,1)\cap \mathbb {Q}$
such that the ordered structures
$(0,1)\cap \mathbb {Q}$
such that the ordered structures
![]() $(J_\alpha ,\le )$
are pairwise non-isomorphic and each embed
$(J_\alpha ,\le )$
are pairwise non-isomorphic and each embed
![]() $(\mathbb {Q}, \leq )$
. For each
$(\mathbb {Q}, \leq )$
. For each
![]() $\alpha $
, let
$\alpha $
, let
![]() $N_\alpha \subseteq N$
have universe
$N_\alpha \subseteq N$
have universe
![]() . As
. As
![]() $(J_\alpha , \leq )$
and
$(J_\alpha , \leq )$
and
![]() $(J_\beta , \leq )$
both embed
$(J_\beta , \leq )$
both embed
![]() $(\mathbb {Q}, \leq )$
, they are bi-embeddable, and these lift to bi-embeddings of
$(\mathbb {Q}, \leq )$
, they are bi-embeddable, and these lift to bi-embeddings of
![]() $N_\alpha $
and
$N_\alpha $
and
![]() $N_\beta $
fixing
$N_\beta $
fixing
![]() $N^*$
pointwise.
$N^*$
pointwise.
It is true that some of the structures
![]() $N_\alpha ,N_\beta $
may be isomorphic, but we will find a subfamily of size
$N_\alpha ,N_\beta $
may be isomorphic, but we will find a subfamily of size
![]() $2^{\aleph _0}$
that are pairwise non-isomorphic, which finishes our argument. Our method will be to prove that for any given
$2^{\aleph _0}$
that are pairwise non-isomorphic, which finishes our argument. Our method will be to prove that for any given
![]() $N_\alpha $
,
$N_\alpha $
,
![]() is countable, which suffices. In particular, we will fix a uniform finite set
is countable, which suffices. In particular, we will fix a uniform finite set
![]() $F \subset N^*$
and prove that when
$F \subset N^*$
and prove that when
![]() $\alpha \neq \beta $
, there is no isomorphism
$\alpha \neq \beta $
, there is no isomorphism
![]() $h:N_\beta \rightarrow N_\alpha $
that fixes F pointwise. Then we cannot have
$h:N_\beta \rightarrow N_\alpha $
that fixes F pointwise. Then we cannot have
![]() $h \colon N_\beta \rightarrow N_\alpha $
and
$h \colon N_\beta \rightarrow N_\alpha $
and
![]() $h' \colon N_{\beta '}\rightarrow N_\alpha $
with
$h' \colon N_{\beta '}\rightarrow N_\alpha $
with
![]() $h(F) = h'(F)$
pointwise, since
$h(F) = h'(F)$
pointwise, since
![]() $h^{-1} \circ h'$
would fix F. As each
$h^{-1} \circ h'$
would fix F. As each
![]() $N_\alpha $
is countable, there are only countably many possible images of F under an isomorphism
$N_\alpha $
is countable, there are only countably many possible images of F under an isomorphism
![]() $h \colon N_\beta \rightarrow N_\alpha $
; hence
$h \colon N_\beta \rightarrow N_\alpha $
; hence
![]() is countable, as required.
is countable, as required.
Constructing F and proving its suitability will take the rest of the section.⊣
To begin, we have the following definition that involves permutations of k-tuples. For a given k-tuple
![]() $\bar {a}_q$
from N and a given
$\bar {a}_q$
from N and a given
![]() $\pi \in Sym(k)$
, let
$\pi \in Sym(k)$
, let
![]() $\pi (\bar {a}_q)$
be the permutation of
$\pi (\bar {a}_q)$
be the permutation of
![]() $\bar {a}$
induced by
$\bar {a}$
induced by
![]() $\pi $
.
$\pi $
.
Definition 3.4. Working in N, a permutation
![]() $\pi \in Sym(k)$
is permissible if for some (equivalently for all, by order indiscernibility)
$\pi \in Sym(k)$
is permissible if for some (equivalently for all, by order indiscernibility)
![]() $q\in (0,1)\cap \mathbb {Q}$
,
$q\in (0,1)\cap \mathbb {Q}$
,
![]() .
.
Equivalently,
![]() $\pi $
is permissible if and only if the map sending
$\pi $
is permissible if and only if the map sending
![]() $\bar {a}_q$
to
$\bar {a}_q$
to
![]() $\pi (\bar {a}_q)$
, and otherwise restricting to the identity, is an automorphism of N.
$\pi (\bar {a}_q)$
, and otherwise restricting to the identity, is an automorphism of N.
The following lemma is easy because
![]() $Sym(k)$
is finite.
$Sym(k)$
is finite.
Lemma 3.5. There is a finite set
![]() $G\subseteq N^*$
such that for any
$G\subseteq N^*$
such that for any
![]() $\pi \in Sym(k)$
,
$\pi \in Sym(k)$
,
![]() $\pi $
is permissible if and only if for some
$\pi $
is permissible if and only if for some
![]() $($
equivalently, for every
$($
equivalently, for every
![]() $)\ q\in (0,1)\cap \mathbb {Q}$
,
$)\ q\in (0,1)\cap \mathbb {Q}$
,
![]() $\mathrm {tp}(\pi (\bar {a}_q)/G)=\mathrm {tp}(\bar {a}_q/G)$
.
$\mathrm {tp}(\pi (\bar {a}_q)/G)=\mathrm {tp}(\bar {a}_q/G)$
.
Proof. Fix any
![]() $q\in (0,1)\cap \mathbb {Q}$
. For each
$q\in (0,1)\cap \mathbb {Q}$
. For each
![]() $\sigma \in Sym(k)$
that is not permissible, choose a finite subset
$\sigma \in Sym(k)$
that is not permissible, choose a finite subset
![]() such that
such that
![]() $\mathrm {tp}(\sigma (\bar {a}_q)/G_{\sigma }^0)\neq \mathrm {tp}(\bar {a}_q/G_{\sigma }^0)$
. By order indiscernibility, we may replace
$\mathrm {tp}(\sigma (\bar {a}_q)/G_{\sigma }^0)\neq \mathrm {tp}(\bar {a}_q/G_{\sigma }^0)$
. By order indiscernibility, we may replace
![]() $G_\sigma ^0$
by a ‘conjugate’
$G_\sigma ^0$
by a ‘conjugate’
![]() $G_\sigma \subseteq N^*$
so that
$G_\sigma \subseteq N^*$
so that
![]() $\mathrm {tp}(\sigma (\bar {a}_q)/G_{\sigma })\neq \mathrm {tp}(\bar {a}_q/G_{\sigma })$
. Then, by order indiscernibility,
$\mathrm {tp}(\sigma (\bar {a}_q)/G_{\sigma })\neq \mathrm {tp}(\bar {a}_q/G_{\sigma })$
. Then, by order indiscernibility,
![]() works not only for q but for any
works not only for q but for any
![]() $q'\in (0,1)\cap \mathbb {Q}$
.⊣
$q'\in (0,1)\cap \mathbb {Q}$
.⊣
Next, we pinpoint a failure of total indiscernibility over M. Since
![]() is strictly order indiscernible over M there is an integer
is strictly order indiscernible over M there is an integer
![]() $\ell \ge 2$
, a permutation
$\ell \ge 2$
, a permutation
![]() $\sigma \in Sym(\ell )$
, and a formula
$\sigma \in Sym(\ell )$
, and a formula
![]() $\theta (\bar {x}_1,\dots ,\bar {x}_\ell ,\bar {m})$
(with
$\theta (\bar {x}_1,\dots ,\bar {x}_\ell ,\bar {m})$
(with
![]() $\bar {m}$
from M and
$\bar {m}$
from M and
![]() $\lg (\bar {x}_i)=k$
for each i) such that
$\lg (\bar {x}_i)=k$
for each i) such that
As
![]() $\sigma $
is a product of transpositions, this implies that there is some i,
$\sigma $
is a product of transpositions, this implies that there is some i,
![]() $1\le i<\ell $
, such that
$1\le i<\ell $
, such that
Translating by i and adding dummy variables as needed, there is some
![]() $r\ge 2$
such that
$r\ge 2$
such that
Let H be the parameters
![]() and let
and let
![]() $\theta (\bar {x},\bar {y})$
be the H-definable formula mentioned above.
$\theta (\bar {x},\bar {y})$
be the H-definable formula mentioned above.
Take
![]() to be our finite subset of
to be our finite subset of
![]() $N^*$
. Put
$N^*$
. Put
![]() $\gamma (\bar {x}):=\bigwedge \mathrm {tp}(\bar {a}_q/F)$
for any
$\gamma (\bar {x}):=\bigwedge \mathrm {tp}(\bar {a}_q/F)$
for any
![]() $q\in (0,1)\cap \mathbb {Q}$
. Let
$q\in (0,1)\cap \mathbb {Q}$
. Let
The following lemma characterizes when
![]() $N\models \delta (\bar {d})$
among all permutations of
$N\models \delta (\bar {d})$
among all permutations of
![]() $\bar {a}_q$
.
$\bar {a}_q$
.
Lemma 3.6.
![]() $($
1
$($
1
![]() $)$
For
$)$
For
![]() $q,r\in [0,1]\cap \mathbb {Q}$
,
$q,r\in [0,1]\cap \mathbb {Q}$
,
![]() $N\models \theta (\bar {a}_q,\bar {a}_r)$
if and only if
$N\models \theta (\bar {a}_q,\bar {a}_r)$
if and only if
![]() $q<r$
.
$q<r$
.
![]() $($
2
$($
2
![]() $)$
For
$)$
For
![]() $q\in \mathbb {Q}$
and
$q\in \mathbb {Q}$
and
![]() $\pi \in Sym(k)$
,
$\pi \in Sym(k)$
,
![]() $N\models \delta (\pi (\bar {a}_q))$
if and only if
$N\models \delta (\pi (\bar {a}_q))$
if and only if
![]() $q\in (0,1)$
and
$q\in (0,1)$
and
![]() $\pi $
is permissible.
$\pi $
is permissible.
Proof. (1) From above, this is true with
![]() $q=0, r=1$
, so the general statement follows by order indiscernibility.
$q=0, r=1$
, so the general statement follows by order indiscernibility.
(2) Suppose
![]() $N\models \delta (\pi (\bar {a}_q))$
. We first argue that
$N\models \delta (\pi (\bar {a}_q))$
. We first argue that
![]() $q\in (0,1)$
. Note that
$q\in (0,1)$
. Note that
![]() $q=0,1$
are forbidden by
$q=0,1$
are forbidden by
![]() $\gamma (\bar {x})$
. If
$\gamma (\bar {x})$
. If
![]() $q<0$
, then as
$q<0$
, then as
![]() $\langle q,-r,\dots ,-1,0,2,\dots ,r\rangle $
has the same order type as
$\langle q,-r,\dots ,-1,0,2,\dots ,r\rangle $
has the same order type as
![]() $\langle q,-r,\dots ,{-}1,1,2,\dots , r\rangle $
, indiscernibility yields
$\langle q,-r,\dots ,{-}1,1,2,\dots , r\rangle $
, indiscernibility yields
so
![]() $N\models \neg \delta (\pi (\bar {a}_q))$
. Arguing similarly,
$N\models \neg \delta (\pi (\bar {a}_q))$
. Arguing similarly,
![]() $N\models \neg \delta (\pi (\bar {a}_q))$
when
$N\models \neg \delta (\pi (\bar {a}_q))$
when
![]() $q>1$
as well. Thus,
$q>1$
as well. Thus,
![]() $q\in (0,1)$
. But now, as
$q\in (0,1)$
. But now, as
![]() $N\models \gamma (\pi (\bar {a}_q))$
we have
$N\models \gamma (\pi (\bar {a}_q))$
we have
![]() $\mathrm {tp}(\pi (\bar {a}_q)/G)=\mathrm {tp}(\bar {a}_q/G)$
, so
$\mathrm {tp}(\pi (\bar {a}_q)/G)=\mathrm {tp}(\bar {a}_q/G)$
, so
![]() $\pi $
is permissible by Lemma 3.5.
$\pi $
is permissible by Lemma 3.5.
Conversely, suppose
![]() $q\in (0,1)$
and
$q\in (0,1)$
and
![]() $\pi $
is permissible. That
$\pi $
is permissible. That
![]() $N\models \delta (\bar {a}_q)$
follows from (1). As
$N\models \delta (\bar {a}_q)$
follows from (1). As
![]() $\pi $
is permissible,
$\pi $
is permissible,
![]() $N\models \delta (\pi (\bar {a}_q))$
as well.⊣
$N\models \delta (\pi (\bar {a}_q))$
as well.⊣
We next show that
![]() $N\models \neg \delta (\bar {d})$
for any
$N\models \neg \delta (\bar {d})$
for any
![]() $\bar {d}\in N^k$
that is not a permutation (permissible or otherwise) of some
$\bar {d}\in N^k$
that is not a permutation (permissible or otherwise) of some
![]() $\bar {a}_q$
. For this, we introduce the notion of a hybrid, which will be an n-tuple for some
$\bar {a}_q$
. For this, we introduce the notion of a hybrid, which will be an n-tuple for some
![]() $n \leq k$
that is not (a permutation of) one of our “intended” tuples
$n \leq k$
that is not (a permutation of) one of our “intended” tuples
![]() $\bar {a}_q$
. In future sections, we will make analogous definitions of “unintended” tuples and prove analogous lemmas to control their behavior.
$\bar {a}_q$
. In future sections, we will make analogous definitions of “unintended” tuples and prove analogous lemmas to control their behavior.
Definition 3.7. Any automorphism
![]() $\sigma $
of
$\sigma $
of
![]() $(\mathbb {Q},\le )$
extends naturally to an automorphism
$(\mathbb {Q},\le )$
extends naturally to an automorphism
![]() $\sigma ^*\in Aut(N)$
that fixes M pointwise, and maps each
$\sigma ^*\in Aut(N)$
that fixes M pointwise, and maps each
![]() $\bar {a}_q$
to
$\bar {a}_q$
to
![]() $\bar {a}_{\sigma (q)}$
. We call these automorphisms of
$\bar {a}_{\sigma (q)}$
. We call these automorphisms of
![]() $Aut(N)$
the standard automorphisms.
$Aut(N)$
the standard automorphisms.
Definition 3.8. For any
![]() $n \leq k$
,
$n \leq k$
,
![]() $\bar {d}\in N^n$
is a hybrid if no permutation of any
$\bar {d}\in N^n$
is a hybrid if no permutation of any
![]() $\bar {a}_q$
is a subsequence of
$\bar {a}_q$
is a subsequence of
![]() $\bar {d}$
.
$\bar {d}$
.
-
• A hybrid
 $\bar {d}$
is from
$\bar {d}$
is from
 $q_1<\dots <q_t$
if
$q_1<\dots <q_t$
if
 $\bar {d}\subseteq M\cup \bar {a}_{q_1}\cup \dots \cup \bar {a}_{q_t}$
, and
$\bar {d}\subseteq M\cup \bar {a}_{q_1}\cup \dots \cup \bar {a}_{q_t}$
, and
 $\bar {d}\cap \bar {a}_{q_i}\neq \emptyset $
for every
$\bar {d}\cap \bar {a}_{q_i}\neq \emptyset $
for every
 $1\le i\le t$
.
$1\le i\le t$
. -
• If
 $\bar {d}$
is from
$\bar {d}$
is from
 $q_1<\dots <q_t$
and
$q_1<\dots <q_t$
and
 $\bar {d}'$
is from
$\bar {d}'$
is from
 $r_1<\dots <r_t$
, we say
$r_1<\dots <r_t$
, we say
 $\bar {d}$
and
$\bar {d}$
and
 $\bar {d}'$
are associated if
$\bar {d}'$
are associated if
 $\sigma ^*(\bar {d})=\bar {d}'$
for some/any standard automorphism
$\sigma ^*(\bar {d})=\bar {d}'$
for some/any standard automorphism
 $\sigma ^*\in Aut(N)$
extending any automorphism
$\sigma ^*\in Aut(N)$
extending any automorphism
 $\sigma \in Aut(\mathbb {Q},\le )$
with
$\sigma \in Aut(\mathbb {Q},\le )$
with
 $\sigma (q_i)=r_i$
for each i.
$\sigma (q_i)=r_i$
for each i.
The next lemma crucially uses that M is array-minimal of index k.
Lemma 3.9. Suppose
![]() $\bar {b}_q$
is a proper subsequence of
$\bar {b}_q$
is a proper subsequence of
![]() $\bar {a}_q$
,
$\bar {a}_q$
,
![]() $\bar {b}_r$
is a proper subsequence of
$\bar {b}_r$
is a proper subsequence of
![]() $\bar {a}_r$
, and
$\bar {a}_r$
, and
![]() $\bar {b}_q$
and
$\bar {b}_q$
and
![]() $\bar {b}_r$
are associated. Then
$\bar {b}_r$
are associated. Then
![]() .
.
Proof. Assume not. Clearly,
![]() $q\neq r$
, so assume
$q\neq r$
, so assume
![]() $q<r$
. Choose a formula
$q<r$
. Choose a formula
![]() $\phi (\bar {x},\bar {e})$
with
$\phi (\bar {x},\bar {e})$
with
![]() such that
such that
Choose a dense/codense subset
![]() $D\subseteq \mathbb {Q}$
and let
$D\subseteq \mathbb {Q}$
and let
![]() $N_0$
be the substructure of N with universe
$N_0$
be the substructure of N with universe
![]() . Clearly,
. Clearly,
![]() $N_0$
is an age-preserving extension of M, so we will obtain a contradiction to M being array-minimal of index k by proving that
$N_0$
is an age-preserving extension of M, so we will obtain a contradiction to M being array-minimal of index k by proving that
![]() $\mathrm {tp}(\bar {b}_{q'}/N_0)\neq \mathrm {tp}(\bar {b}_{r'}/N_0)$
for all pairs
$\mathrm {tp}(\bar {b}_{q'}/N_0)\neq \mathrm {tp}(\bar {b}_{r'}/N_0)$
for all pairs
![]() $q'<r'$
from D, where
$q'<r'$
from D, where
![]() $\bar {b}_{q'}$
is the subsequence of
$\bar {b}_{q'}$
is the subsequence of
![]() $\bar {a}_{q'}$
associated with both
$\bar {a}_{q'}$
associated with both
![]() $\bar {b}_q$
and
$\bar {b}_q$
and
![]() $\bar {b}_r$
and similarly for
$\bar {b}_r$
and similarly for
![]() $\bar {b}_{r'}$
. (That each of these types is coordinate-wise non-algebraic is immediate, since each
$\bar {b}_{r'}$
. (That each of these types is coordinate-wise non-algebraic is immediate, since each
![]() $\bar {b}_{q'}$
is disjoint from
$\bar {b}_{q'}$
is disjoint from
![]() $N_0$
. Thus, each of these supports an infinite array by Lemma 2.8.)
$N_0$
. Thus, each of these supports an infinite array by Lemma 2.8.)
To see this, fix
![]() $q'<r'$
from D, and let
$q'<r'$
from D, and let
![]() $\bar {e}$
be from
$\bar {e}$
be from
![]() $s_1 < \dots < s_t$
. As D is dense/codense in
$s_1 < \dots < s_t$
. As D is dense/codense in
![]() $\mathbb {Q}$
, there is some
$\mathbb {Q}$
, there is some
![]() $\sigma \in Aut(\mathbb {Q}, \leq )$
sending
$\sigma \in Aut(\mathbb {Q}, \leq )$
sending
![]() $q \mapsto q'$
,
$q \mapsto q'$
,
![]() $r \mapsto r'$
, and
$r \mapsto r'$
, and
![]() $s_1, \dots , s_t$
into
$s_1, \dots , s_t$
into
![]() $(\mathbb {Q} \backslash D)$
. Letting
$(\mathbb {Q} \backslash D)$
. Letting
![]() $\sigma ^* \in Aut(N)$
be the corresponding standard automorphism, we have
$\sigma ^* \in Aut(N)$
be the corresponding standard automorphism, we have
As
![]() $\sigma ^*(\bar {e}) \subset N_0$
, we have
$\sigma ^*(\bar {e}) \subset N_0$
, we have
![]() $\mathrm {tp}(\bar {b}_{q'}/N_0)\neq \mathrm {tp}(\bar {b}_{r'}/N_0)$
, as required.⊣
$\mathrm {tp}(\bar {b}_{q'}/N_0)\neq \mathrm {tp}(\bar {b}_{r'}/N_0)$
, as required.⊣
Next, we discuss arbitrary hybrids. In the assumptions of the following lemma, the fact that
![]() $\bar {d},\bar {d}'$
are associated implies that the t is the same in both places.
$\bar {d},\bar {d}'$
are associated implies that the t is the same in both places.
Lemma 3.10. For
![]() $n \leq k$
, suppose
$n \leq k$
, suppose
![]() $\bar {d},\bar {d}'\in N^n$
are associated hybrids with
$\bar {d},\bar {d}'\in N^n$
are associated hybrids with
![]() $\bar {d}$
from
$\bar {d}$
from
![]() $q_1<\dots <q_t$
and
$q_1<\dots <q_t$
and
![]() $\bar {d}'$
from
$\bar {d}'$
from
![]() $r_1<\dots <r_t$
. Then
$r_1<\dots <r_t$
. Then
![]() $\mathrm {tp}(\bar {d}/N_0)=\mathrm {tp}(\bar {d}'/N_0)$
, where
$\mathrm {tp}(\bar {d}/N_0)=\mathrm {tp}(\bar {d}'/N_0)$
, where
![]() .
.
Proof. This will follow easily from the following special case.
Claim. The statement holds if
![]() and
and
![]() are disjoint.
are disjoint.
Proof of Claim. Under this additional assumption, we argue by induction on t. First, if
![]() $t=0$
, then
$t=0$
, then
![]() $\bar {d}\subseteq M$
. As
$\bar {d}\subseteq M$
. As
![]() $\bar {d}'$
is associated with
$\bar {d}'$
is associated with
![]() $\bar {d}$
,
$\bar {d}$
,
![]() $\bar {d}'=\bar {d}$
so the statement is trivially true.
$\bar {d}'=\bar {d}$
so the statement is trivially true.
Now assume that the statement is true for
![]() $t-1$
. Write
$t-1$
. Write
![]() $\bar {d}:=\bar {h}\bar {b}$
, where
$\bar {d}:=\bar {h}\bar {b}$
, where
![]() $\bar {h}$
is from
$\bar {h}$
is from
![]() $q_1<\dots <q_{t-1}$
and
$q_1<\dots <q_{t-1}$
and
![]() $\bar {b}$
is from
$\bar {b}$
is from
![]() $q_t$
. Let
$q_t$
. Let
![]() $\sigma ^*\in Aut(N)$
be a standard automorphism extending any automorphism
$\sigma ^*\in Aut(N)$
be a standard automorphism extending any automorphism
![]() $\sigma \in Aut(\mathbb {Q},\le )$
extending the map
$\sigma \in Aut(\mathbb {Q},\le )$
extending the map
![]() $q_i\mapsto r_i$
for each i. Let
$q_i\mapsto r_i$
for each i. Let
![]() $\bar {h}':=\sigma ^*(\bar {h})$
and
$\bar {h}':=\sigma ^*(\bar {h})$
and
![]() $\bar {b}':=\sigma ^*(\bar {b})$
. As
$\bar {b}':=\sigma ^*(\bar {b})$
. As
![]() $\bar {d}$
is a hybrid, we have that
$\bar {d}$
is a hybrid, we have that
![]() $\bar {b}$
is a proper subsequence of
$\bar {b}$
is a proper subsequence of
![]() $\bar {a}_{q_t}$
(up to a permutation, which may be ignored), and so
$\bar {a}_{q_t}$
(up to a permutation, which may be ignored), and so
![]() $\bar {b}'$
is also a proper subsequence of
$\bar {b}'$
is also a proper subsequence of
![]() $\bar {a}_{r_t}$
, associated with
$\bar {a}_{r_t}$
, associated with
![]() $\bar {b}$
.
$\bar {b}$
.
To see that
![]() $\mathrm {tp}(\bar {d}/N_0)=\mathrm {tp}(\bar {d}'/N_0)$
, choose any
$\mathrm {tp}(\bar {d}/N_0)=\mathrm {tp}(\bar {d}'/N_0)$
, choose any
![]() $\phi (\bar {x},\bar {e})\in \mathrm {tp}(\bar {d}/N_0)$
. Thus
$\phi (\bar {x},\bar {e})\in \mathrm {tp}(\bar {d}/N_0)$
. Thus
![]() $N\models \phi (\bar {h},\bar {b},\bar {e})$
. By our assumption that
$N\models \phi (\bar {h},\bar {b},\bar {e})$
. By our assumption that
![]() is disjoint from
is disjoint from
![]() , we have
, we have
![]() , and so
, and so
![]() $N\models \phi (\bar {h},\bar {b}',\bar {e})$
by Lemma 3.9. But now, as
$N\models \phi (\bar {h},\bar {b}',\bar {e})$
by Lemma 3.9. But now, as
![]() $\bar {h}$
is a hybrid from
$\bar {h}$
is a hybrid from
![]() $q_1<\dots <q_{t-1}$
that is associated with
$q_1<\dots <q_{t-1}$
that is associated with
![]() $\bar {h}'$
, our inductive hypothesis implies that
$\bar {h}'$
, our inductive hypothesis implies that
![]() $N\models \phi (\bar {h}',\bar {b}',\bar {e})$
. Thus,
$N\models \phi (\bar {h}',\bar {b}',\bar {e})$
. Thus,
![]() $\phi (\bar {x},\bar {e})\in \mathrm {tp}(\bar {d}'/N_0)$
as needed.◊
$\phi (\bar {x},\bar {e})\in \mathrm {tp}(\bar {d}'/N_0)$
as needed.◊
For the general case where
![]() and
and
![]() need not be disjoint, choose any
need not be disjoint, choose any
![]() $\phi (\bar {x},\bar {e})\in \mathrm {tp}(\bar {d}/N_0)$
. Choose
$\phi (\bar {x},\bar {e})\in \mathrm {tp}(\bar {d}/N_0)$
. Choose
![]() $s_1<\dots <s_t$
disjoint from
$s_1<\dots <s_t$
disjoint from
![]() and such that
and such that
![]() $\bar {e}$
is disjoint from
$\bar {e}$
is disjoint from
![]() $\bar {a}_{s_1}\cup \dots \cup \bar {a}_{s_t}$
. Let
$\bar {a}_{s_1}\cup \dots \cup \bar {a}_{s_t}$
. Let
![]() $\bar {d}"$
be the hybrid from
$\bar {d}"$
be the hybrid from
![]() $s_1<\dots <s_t$
associated with both
$s_1<\dots <s_t$
associated with both
![]() $\bar {d}$
and
$\bar {d}$
and
![]() $\bar {d}'$
. Because of the disjointness, we can apply the claim to the pairs
$\bar {d}'$
. Because of the disjointness, we can apply the claim to the pairs
![]() $\bar {d},\bar {d}"$
and
$\bar {d},\bar {d}"$
and
![]() $\bar {d}',\bar {d}"$
to obtain
$\bar {d}',\bar {d}"$
to obtain
Thus,
![]() $\phi (\bar {x},\bar {e})\in \mathrm {tp}(\bar {d}'/N_0)$
as required.⊣
$\phi (\bar {x},\bar {e})\in \mathrm {tp}(\bar {d}'/N_0)$
as required.⊣
Finally, we can finish off our problem of identifying realizations of
![]() $\delta (\bar {x})$
in
$\delta (\bar {x})$
in
![]() $N^k$
.
$N^k$
.
Corollary 3.11. For
![]() $\bar {d}\in N^k$
,
$\bar {d}\in N^k$
,
![]() $N\models \delta (\bar {d})$
if and only if
$N\models \delta (\bar {d})$
if and only if
![]() $\bar {d}=\pi (\bar {a}_q)$
for some
$\bar {d}=\pi (\bar {a}_q)$
for some
![]() $q\in (0,1)\cap \mathbb {Q}$
and some permissible
$q\in (0,1)\cap \mathbb {Q}$
and some permissible
![]() $\pi \in Sym(k)$
.
$\pi \in Sym(k)$
.
Proof. First, if
![]() $\bar {d}$
is
$\bar {d}$
is
![]() $\pi (\bar {a}_q)$
for some
$\pi (\bar {a}_q)$
for some
![]() $q\in \mathbb {Q}$
and
$q\in \mathbb {Q}$
and
![]() $\pi \in Sym(k)$
, this is proved in Lemma 3.6. So assume
$\pi \in Sym(k)$
, this is proved in Lemma 3.6. So assume
![]() $\bar {d}\in N^k$
is not a permutation of any
$\bar {d}\in N^k$
is not a permutation of any
![]() $\bar {a}_q$
, i.e.,
$\bar {a}_q$
, i.e.,
![]() $\bar {d}$
is a hybrid. We argue that
$\bar {d}$
is a hybrid. We argue that
![]() $N\models \neg \delta (\bar {d})$
. Say
$N\models \neg \delta (\bar {d})$
. Say
![]() $\bar {d}$
is from
$\bar {d}$
is from
![]() $q_1<\dots <q_t$
. Choose
$q_1<\dots <q_t$
. Choose
![]() $r_1<\dots <r_t<0$
from
$r_1<\dots <r_t<0$
from
![]() $\mathbb {Q}$
, and let
$\mathbb {Q}$
, and let
![]() $\bar {d}'$
be associated with
$\bar {d}'$
be associated with
![]() $\bar {d}$
from
$\bar {d}$
from
![]() $r_1<\dots <r_t$
. By order indiscernibility,
$r_1<\dots <r_t$
. By order indiscernibility,
In particular,
![]() $N\models \neg \delta (\bar {d}')$
. From the definition of
$N\models \neg \delta (\bar {d}')$
. From the definition of
![]() $\delta (\bar {x})$
, we may assume
$\delta (\bar {x})$
, we may assume
![]() $\bar {d}\cap F=\emptyset $
, and so by Lemma 3.10 we also have
$\bar {d}\cap F=\emptyset $
, and so by Lemma 3.10 we also have
so
![]() $N\models \neg \delta (\bar {d})$
as claimed.⊣
$N\models \neg \delta (\bar {d})$
as claimed.⊣
The following lemma will finish the proof of Proposition 3.3.
Lemma 3.12. If
![]() $f:N_\alpha \rightarrow N_\beta $
is an isomorphism fixing F pointwise, then
$f:N_\alpha \rightarrow N_\beta $
is an isomorphism fixing F pointwise, then
![]() $(J_\alpha ,\le) \cong (J_\beta ,\le );$
hence
$(J_\alpha ,\le) \cong (J_\beta ,\le );$
hence
![]() $\alpha =\beta $
.
$\alpha =\beta $
.
Proof. We define a map
![]() $f^*:J_\alpha \rightarrow J_\beta $
as follows. Given
$f^*:J_\alpha \rightarrow J_\beta $
as follows. Given
![]() $q\in J_\alpha $
, note that
$q\in J_\alpha $
, note that
![]() $N\models \delta (\bar {a}_q)$
. Thus,
$N\models \delta (\bar {a}_q)$
. Thus,
![]() $N\models \delta (f(\bar {a}_q))$
as well. By Corollary 3.11
$N\models \delta (f(\bar {a}_q))$
as well. By Corollary 3.11
![]() $f(\bar {a}_q)=\pi (\bar {a}_s)$
for some
$f(\bar {a}_q)=\pi (\bar {a}_s)$
for some
![]() $s\in (0,1)$
and some permissible permutation
$s\in (0,1)$
and some permissible permutation
![]() $\pi $
. As
$\pi $
. As
![]() $f(\bar {a}_q)\subseteq N_\beta $
, we must have
$f(\bar {a}_q)\subseteq N_\beta $
, we must have
![]() $s\in J_\beta $
. Put
$s\in J_\beta $
. Put
![]() $f^*(q):=s$
. It is clear that
$f^*(q):=s$
. It is clear that
![]() $f^*:J_\alpha \rightarrow J_\beta $
is bijective.
$f^*:J_\alpha \rightarrow J_\beta $
is bijective.
To see that
![]() $f^*$
is order-preserving, choose
$f^*$
is order-preserving, choose
![]() $q<q'$
from
$q<q'$
from
![]() $J_\alpha $
. Write
$J_\alpha $
. Write
![]() $f(\bar {a}_q)$
as
$f(\bar {a}_q)$
as
![]() $\pi (\bar {a}_s)$
and write
$\pi (\bar {a}_s)$
and write
![]() $f(\bar {a}_{q'})$
as
$f(\bar {a}_{q'})$
as
![]() $\pi '(\bar {a}_{s'})$
. As both
$\pi '(\bar {a}_{s'})$
. As both
![]() $\pi ,\pi '$
are permissible, there is a
$\pi ,\pi '$
are permissible, there is a
![]() $\sigma \in Aut(N)$
sending
$\sigma \in Aut(N)$
sending
![]() $\pi (\bar {a}_s)\mapsto \bar {a}_s$
,
$\pi (\bar {a}_s)\mapsto \bar {a}_s$
,
![]() $\pi '(\bar {a}_{s'})\mapsto \bar {a}_{s'}$
, and fixing everything else. Then the composition
$\pi '(\bar {a}_{s'})\mapsto \bar {a}_{s'}$
, and fixing everything else. Then the composition
![]() $g:= \sigma \circ f:N_\alpha \rightarrow N_\beta $
is an isomorphism fixing F pointwise sending
$g:= \sigma \circ f:N_\alpha \rightarrow N_\beta $
is an isomorphism fixing F pointwise sending
![]() $\bar {a}_q\mapsto \bar {a}_s$
,
$\bar {a}_q\mapsto \bar {a}_s$
,
![]() $\bar {a}_{q'}\mapsto \bar {a}_{s'}$
.
$\bar {a}_{q'}\mapsto \bar {a}_{s'}$
.
By Lemma 3.6(1),
![]() $N\models \theta (\bar {a}_q,\bar {a}_{q'})$
. As
$N\models \theta (\bar {a}_q,\bar {a}_{q'})$
. As
![]() $\theta $
is quantifier-free,
$\theta $
is quantifier-free,
![]() $N_\alpha \models \theta (\bar {a}_q,\bar {a}_{q'})$
. Since g is an isomorphism fixing F pointwise,
$N_\alpha \models \theta (\bar {a}_q,\bar {a}_{q'})$
. Since g is an isomorphism fixing F pointwise,
![]() $N_\beta \models \theta (\bar {a}_{s},\bar {a}_{s'})$
, and hence
$N_\beta \models \theta (\bar {a}_{s},\bar {a}_{s'})$
, and hence
![]() $N\models \theta (\bar {a}_{s},\bar {a}_{s'})$
. By Lemma 3.6(1) again,
$N\models \theta (\bar {a}_{s},\bar {a}_{s'})$
. By Lemma 3.6(1) again,
![]() $s<s'$
. That is,
$s<s'$
. That is,
![]() $f^*(q)<f^*(q')$
.⊣
$f^*(q)<f^*(q')$
.⊣
4
 $k$
-cliques
$k$
-cliques
In this section, we introduce k-cliques, which will serve the function of equivalence classes from Case 2 of Section 1.1.
Fix a finite relational
![]() ${\mathcal L}$
with maximal arity r and an ambient
${\mathcal L}$
with maximal arity r and an ambient
![]() ${\mathcal L}$
-structure M throughout this section.
${\mathcal L}$
-structure M throughout this section.
For
![]() $n\ge r$
, call a quantifier-free
$n\ge r$
, call a quantifier-free
![]() ${\mathcal L}$
-formula
${\mathcal L}$
-formula
![]() $\phi (x_1,\dots ,x_n)$
q.f.-complete if
$\phi (x_1,\dots ,x_n)$
q.f.-complete if
![]() $\phi (x_1,\dots ,x_n)$
decides every atomic
$\phi (x_1,\dots ,x_n)$
decides every atomic
![]() $R(\bar {y})$
for every permutation
$R(\bar {y})$
for every permutation
![]() $\bar {y}$
of a subsequence of
$\bar {y}$
of a subsequence of
![]() $(x_1,\dots ,x_n)$
. As
$(x_1,\dots ,x_n)$
. As
![]() ${\mathcal L}$
is finite relational, there is a finite set
${\mathcal L}$
is finite relational, there is a finite set
![]() ${\mathcal S}_n$
of q.f.-complete
${\mathcal S}_n$
of q.f.-complete
![]() $\phi (x_1,\dots ,x_n)$
such that for every
$\phi (x_1,\dots ,x_n)$
such that for every
![]() ${\mathcal L}$
-structure M and every
${\mathcal L}$
-structure M and every
![]() $\bar {c}\in M^n$
,
$\bar {c}\in M^n$
,
![]() $\mathrm {tp}(\bar {c})$
contains precisely one element of
$\mathrm {tp}(\bar {c})$
contains precisely one element of
![]() ${\mathcal S}_n$
. Fix such a set
${\mathcal S}_n$
. Fix such a set
![]() ${\mathcal S}_n$
for every
${\mathcal S}_n$
for every
![]() $n\ge r$
.
$n\ge r$
.
Definition 4.1. Fix
![]() $k\ge 1$
and let
$k\ge 1$
and let
![]() .
.
-
• A pair
 $\bar {a},\bar {b}\in M^{(k)}$
is exchangeable, written
$\bar {a},\bar {b}\in M^{(k)}$
is exchangeable, written
 $\bar {a} \sim \bar {b}$
, if
$\bar {a} \sim \bar {b}$
, if
 $\bar {a}\cap \bar {b}=\emptyset $
and
$\bar {a}\cap \bar {b}=\emptyset $
and
 .
. -
• A k-clique is a non-empty set
 such that
such that
 $\bar {a}_i,\bar {a}_j$
are exchangeable whenever
$\bar {a}_i,\bar {a}_j$
are exchangeable whenever
 $i \neq j$
.
$i \neq j$
. -
• The size of
 ${\mathcal A}$
is simply its cardinality
${\mathcal A}$
is simply its cardinality
 $|{\mathcal A}|$
.
$|{\mathcal A}|$
. -
• Given a k-clique
 ${\mathcal A}$
, we denote the set of all
${\mathcal A}$
, we denote the set of all
 $a\in M$
such that
$a\in M$
such that
 $a\in \bar {a}_i$
for some
$a\in \bar {a}_i$
for some
 $\bar {a}_i\in {\mathcal A}$
by
$\bar {a}_i\in {\mathcal A}$
by
 $\bigcup {\mathcal A}$
. Because of the disjointness,
$\bigcup {\mathcal A}$
. Because of the disjointness,
 $|\bigcup {\mathcal A}|=k\cdot |{\mathcal A}|$
.
$|\bigcup {\mathcal A}|=k\cdot |{\mathcal A}|$
.
Remark 4.2. Similar to Definition 3.4, for all
![]() $\bar {a},\bar {b}\in M^{(k)}$
with
$\bar {a},\bar {b}\in M^{(k)}$
with
![]() $\bar {a}\cap \bar {b}=\emptyset $
,
$\bar {a}\cap \bar {b}=\emptyset $
,
![]() $\bar {a}$
and
$\bar {a}$
and
![]() $\bar {b}$
are exchangeable if and only if the bijection swapping them is an automorphism of M if and only if
$\bar {b}$
are exchangeable if and only if the bijection swapping them is an automorphism of M if and only if
for every
![]() $\phi (\bar {x}_1,\bar {x}_2,\bar {y})\in {\mathcal S}_{2k+r}$
with
$\phi (\bar {x}_1,\bar {x}_2,\bar {y})\in {\mathcal S}_{2k+r}$
with
![]() $\lg (\bar {y})=r$
. As
$\lg (\bar {y})=r$
. As
![]() ${\mathcal S}_{2k+r}$
is finite, it follows that exchangeability is definable on
${\mathcal S}_{2k+r}$
is finite, it follows that exchangeability is definable on
![]() $M^{(k)}$
. However, unless
$M^{(k)}$
. However, unless
![]() $k=1$
exchangeability need not be transitive, due to the disjointness condition.
$k=1$
exchangeability need not be transitive, due to the disjointness condition.
Definition 4.3. A set of disjoint k-tuples
![]() is totally indiscernible over its complement if it is totally indiscernible over
is totally indiscernible over its complement if it is totally indiscernible over
![]() $M \backslash \bigcup A$
.
$M \backslash \bigcup A$
.
Lemma 4.4. Let
![]() ${\mathcal A}\subseteq M^{(k)}$
be totally indiscernible over its complement, and let
${\mathcal A}\subseteq M^{(k)}$
be totally indiscernible over its complement, and let
![]() ${\mathcal B} \subset {\mathcal A}$
. Then
${\mathcal B} \subset {\mathcal A}$
. Then
![]() ${\mathcal B}$
is totally indiscernible over its complement.
${\mathcal B}$
is totally indiscernible over its complement.
Proof. Let
![]() ,
,
![]() and let
and let
![]() . By relabeling, let
. By relabeling, let
![]() $\ell $
be such that
$\ell $
be such that
![]() $c_i \in \bigcup {\mathcal A}$
iff
$c_i \in \bigcup {\mathcal A}$
iff
![]() $i \leq \ell $
, and let
$i \leq \ell $
, and let
![]() $\bar {a}_1, \dots , \bar {a}_j \in {\mathcal A}$
be such that
$\bar {a}_1, \dots , \bar {a}_j \in {\mathcal A}$
be such that
![]() $c_i \in \bar {a}_1 \cup \dots \cup \bar {a}_j$
for
$c_i \in \bar {a}_1 \cup \dots \cup \bar {a}_j$
for
![]() $i \leq \ell $
.
$i \leq \ell $
.
As
![]() ${\mathcal A}$
is totally indiscernible over its complement, we have
${\mathcal A}$
is totally indiscernible over its complement, we have
Thus, as desired, we have
⊣
Proposition 4.5. Let
![]() ${\mathcal A}\subseteq M^{(k)}$
be pairwise disjoint. Then
${\mathcal A}\subseteq M^{(k)}$
be pairwise disjoint. Then
![]() ${\mathcal A}$
is totally indiscernible over its complement if and only if
${\mathcal A}$
is totally indiscernible over its complement if and only if
![]() ${\mathcal A}$
is a k-clique.
${\mathcal A}$
is a k-clique.
Proof.
![]() $(\Rightarrow )$
Suppose
$(\Rightarrow )$
Suppose
![]() ${\mathcal A}$
is totally indiscernible over its complement, and let
${\mathcal A}$
is totally indiscernible over its complement, and let
![]() $\bar {a}_i, \bar {a}_j \in {\mathcal A}$
. Then by Lemma 4.4,
$\bar {a}_i, \bar {a}_j \in {\mathcal A}$
. Then by Lemma 4.4,
![]() is totally indiscernible over its complement. Thus
is totally indiscernible over its complement. Thus
![]() $\bar {a}_i$
and
$\bar {a}_i$
and
![]() $\bar {a}_j$
are exchangeable.
$\bar {a}_j$
are exchangeable.
![]() $(\Leftarrow )$
Suppose
$(\Leftarrow )$
Suppose
![]() is a k-clique. Let
is a k-clique. Let
![]() $(i_1, \dots , i_n)$
,
$(i_1, \dots , i_n)$
,
![]() $(i_1',\dots , i_n')\in I^n$
. We proceed by induction on
$(i_1',\dots , i_n')\in I^n$
. We proceed by induction on
![]() .
.
If
![]() $m=0$
then there is some
$m=0$
then there is some
![]() $\sigma \in Sym(n)$
such that
$\sigma \in Sym(n)$
such that
![]() $\sigma (i_1, \dots , i_n) = (i^{\prime }_1, \dots , i^{\prime }_n)$
. As
$\sigma (i_1, \dots , i_n) = (i^{\prime }_1, \dots , i^{\prime }_n)$
. As
![]() $\sigma $
can be written as a product of transpositions, we have
$\sigma $
can be written as a product of transpositions, we have
![]() .
.
Now suppose
![]() $m = \ell +1$
. After permuting the tuples, which we have seen does not affect their type, we may suppose
$m = \ell +1$
. After permuting the tuples, which we have seen does not affect their type, we may suppose
![]() and
and
![]() . Using that
. Using that
![]() $a_{i_1}, a_{i^{\prime }_1}$
are exchangeable for the first equality and the inductive hypothesis for the second, we have
$a_{i_1}, a_{i^{\prime }_1}$
are exchangeable for the first equality and the inductive hypothesis for the second, we have
 .⊣
.⊣
Lemma 4.6. Suppose
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal B}$
are k-cliques,
${\mathcal B}$
are k-cliques,
![]() ${\mathcal A}\cap {\mathcal B} \neq \emptyset $
, and
${\mathcal A}\cap {\mathcal B} \neq \emptyset $
, and
![]() $\bigcup ({\mathcal A} \backslash {\mathcal B}) \cap \bigcup ({\mathcal B}\backslash {\mathcal A}) = \emptyset $
. Then
$\bigcup ({\mathcal A} \backslash {\mathcal B}) \cap \bigcup ({\mathcal B}\backslash {\mathcal A}) = \emptyset $
. Then
![]() ${\mathcal A}\cup {\mathcal B}$
is a k-clique.
${\mathcal A}\cup {\mathcal B}$
is a k-clique.
Proof. First, we show distinct tuples
![]() $\bar {a}, \bar {b} \in {\mathcal A} \cup {\mathcal B}$
are disjoint. If
$\bar {a}, \bar {b} \in {\mathcal A} \cup {\mathcal B}$
are disjoint. If
![]() $\bar {a}, \bar {b} \in {\mathcal A}$
(or
$\bar {a}, \bar {b} \in {\mathcal A}$
(or
![]() $\bar {a}, \bar {b} \in {\mathcal B}$
), this follows from the definition of k-cliques. Otherwise
$\bar {a}, \bar {b} \in {\mathcal B}$
), this follows from the definition of k-cliques. Otherwise
![]() $\bar {a} \in ({\mathcal A} \backslash {\mathcal B})$
and
$\bar {a} \in ({\mathcal A} \backslash {\mathcal B})$
and
![]() $\bar {b} \in ({\mathcal B} \backslash {\mathcal A})$
, and so are disjoint by the last assumption.
$\bar {b} \in ({\mathcal B} \backslash {\mathcal A})$
, and so are disjoint by the last assumption.
Let
![]() and
and
![]() , and choose
, and choose
![]() $\bar {c} \in {\mathcal A} \cap {\mathcal B}$
. Let
$\bar {c} \in {\mathcal A} \cap {\mathcal B}$
. Let
![]() $Y = M \backslash (\bar {a}\cup \bar {b}\cup \bar {c})$
. By a sequence of transpositions, each involving
$Y = M \backslash (\bar {a}\cup \bar {b}\cup \bar {c})$
. By a sequence of transpositions, each involving
![]() $\bar {c}$
, we have
$\bar {c}$
, we have
Thus
![]() $\mathrm {tp}(\bar {a}\bar {b}/Y\bar {c}) = \mathrm {tp}(\bar {b}\bar {a}/Y\bar {c})$
, and so
$\mathrm {tp}(\bar {a}\bar {b}/Y\bar {c}) = \mathrm {tp}(\bar {b}\bar {a}/Y\bar {c})$
, and so
![]() $\bar {a} \sim \bar {b}$
, as desired.⊣
$\bar {a} \sim \bar {b}$
, as desired.⊣
Infinite k-cliques
![]() ${\mathcal A}$
in M give rise to types that support infinite arrays.
${\mathcal A}$
in M give rise to types that support infinite arrays.
Definition 4.7. Let
![]() ${\mathcal A}$
be an infinite k-clique and let
${\mathcal A}$
be an infinite k-clique and let
![]() $\bar {x}=(x_1,\dots ,x_k)$
. The average type of
$\bar {x}=(x_1,\dots ,x_k)$
. The average type of
![]() ${\mathcal A}$
, written
${\mathcal A}$
, written
![]() $Av_{{\mathcal A}}(\bar {x})$
, is the set
$Av_{{\mathcal A}}(\bar {x})$
, is the set
Lemma 4.8. If
![]() ${\mathcal A}$
is an infinite k-clique in M, then
${\mathcal A}$
is an infinite k-clique in M, then
![]() $Av_{\mathcal A}(\bar {x})$
is well-defined and
$Av_{\mathcal A}(\bar {x})$
is well-defined and
![]() $Av_{{\mathcal A}}(\bar {x})\in \mathrm {Supp}_k(M)$
.
$Av_{{\mathcal A}}(\bar {x})\in \mathrm {Supp}_k(M)$
.
Proof. For well-definedness, we must check the “some/all” claim implicit in the definition. As
![]() ${\mathcal A}$
is an infinite k-clique,
${\mathcal A}$
is an infinite k-clique,
![]() $\bar {a},\bar {a}'\in {\mathcal A}$
are exchangeable; hence
$\bar {a},\bar {a}'\in {\mathcal A}$
are exchangeable; hence
![]() $\mathrm {tp}(\bar {a}/\bar {e})=\mathrm {tp}(\bar {a}'/\bar {e})$
whenever
$\mathrm {tp}(\bar {a}/\bar {e})=\mathrm {tp}(\bar {a}'/\bar {e})$
whenever
![]() $\bar {a} \cap \bar {e} = \emptyset $
. It is easily verified that it is a complete (quantifier-free) type over M. As any finite subset of
$\bar {a} \cap \bar {e} = \emptyset $
. It is easily verified that it is a complete (quantifier-free) type over M. As any finite subset of
![]() $Av_{{\mathcal A}}(\bar {x})$
is realized by infinitely many
$Av_{{\mathcal A}}(\bar {x})$
is realized by infinitely many
![]() $\bar {a}\in {\mathcal A}$
, we see that
$\bar {a}\in {\mathcal A}$
, we see that
![]() $Av_{{\mathcal A}}(\bar {x})\in \mathrm {Supp}_k(M)$
.⊣
$Av_{{\mathcal A}}(\bar {x})\in \mathrm {Supp}_k(M)$
.⊣
For the remainder of this section, fix an integer
![]() $k\ge 1$
.
$k\ge 1$
.
Definition 4.9. Let M be any
![]() ${\mathcal L}$
-structure.
${\mathcal L}$
-structure.
-
• For any
 $k'\le k$
, call a
$k'\le k$
, call a
 $k'$
-clique
$k'$
-clique
 ${\mathcal A}$
in M sufficiently large if
${\mathcal A}$
in M sufficiently large if
 $|{\mathcal A}|>2k+r$
.
$|{\mathcal A}|>2k+r$
. -
• An extension
 $N\supseteq M$
is
$N\supseteq M$
is
 $(\le k)$
-clique-preserving if, for every
$(\le k)$
-clique-preserving if, for every
 $k'\le k$
, every sufficiently large
$k'\le k$
, every sufficiently large
 $k'$
-clique
$k'$
-clique
 ${\mathcal A}$
in M remains a
${\mathcal A}$
in M remains a
 $k'$
-clique in N.
$k'$
-clique in N.
We will see two ways of obtaining
![]() $(\le k)$
-clique-preserving extensions of M. The first follows from the definability of exchangeability.
$(\le k)$
-clique-preserving extensions of M. The first follows from the definability of exchangeability.
Remark 4.10. If
![]() $M^*\succeq M$
, then since exchangeability is definable,
$M^*\succeq M$
, then since exchangeability is definable,
![]() $M^*$
will be both age-preserving and
$M^*$
will be both age-preserving and
![]() $(\le k)$
-clique-preserving. Moreover, any substructure N satisfying
$(\le k)$
-clique-preserving. Moreover, any substructure N satisfying
![]() $M\subseteq N\subseteq M^*$
will also be an age-preserving,
$M\subseteq N\subseteq M^*$
will also be an age-preserving,
![]() $(\le k)$
-clique-preserving extension of M.
$(\le k)$
-clique-preserving extension of M.
The second method involves extending existing, sufficiently large cliques.
Definition 4.11. Fix an
![]() ${\mathcal L}$
-structure M and recall k is fixed throughout.
${\mathcal L}$
-structure M and recall k is fixed throughout.
-
1. A simple clique extension of M is an extension N with universe
 $M\cup \bigcup {\mathcal C}$
, where for some
$M\cup \bigcup {\mathcal C}$
, where for some
 $k'\le k$
,
$k'\le k$
,
 ${\mathcal C}$
is a
${\mathcal C}$
is a
 $k'$
-clique in N extending some sufficiently large
$k'$
-clique in N extending some sufficiently large
 $k'$
-clique
$k'$
-clique
 ${\mathcal A}$
in M.
${\mathcal A}$
in M. -
2. A clique extension of M is a continuous, nested union
 $\bigcup N_\alpha $
of simple clique extensions, i.e.,
$\bigcup N_\alpha $
of simple clique extensions, i.e.,
 $N_0=M$
,
$N_0=M$
,
 $N_{\alpha +1}$
is a simple clique extension of M, and
$N_{\alpha +1}$
is a simple clique extension of M, and
 $N_\lambda =\bigcup _{\alpha <\lambda } N_\alpha $
for limit
$N_\lambda =\bigcup _{\alpha <\lambda } N_\alpha $
for limit
 $\lambda $
.
$\lambda $
.
Lemma 4.12. Every clique extension
![]() $N\supseteq M$
is
$N\supseteq M$
is
![]() $(\le k)$
-clique-preserving.
$(\le k)$
-clique-preserving.
Proof. Arguing by induction on the length of the chain, it suffices to show this when N is a simple clique extension of M. Similarly, arguing by induction on
![]() , it suffices to show this when
, it suffices to show this when
![]() and
and
![]() . So choose any
. So choose any
![]() $k'\le k$
and any
$k'\le k$
and any
![]() $k'$
-clique
$k'$
-clique
![]() ${\mathcal B}$
in M. To see that
${\mathcal B}$
in M. To see that
![]() ${\mathcal B}$
remains a
${\mathcal B}$
remains a
![]() $k'$
-clique in N, choose
$k'$
-clique in N, choose
![]() $\bar {b},\bar {b}'\in {\mathcal B}$
and
$\bar {b},\bar {b}'\in {\mathcal B}$
and
![]() . It suffices to show that
. It suffices to show that
![]() $N\models \phi (\bar {b},\bar {b}',\bar {h})\leftrightarrow \phi (\bar {b}',\bar {b},\bar {h})$
for every
$N\models \phi (\bar {b},\bar {b}',\bar {h})\leftrightarrow \phi (\bar {b}',\bar {b},\bar {h})$
for every
![]() $\phi \in {\mathcal S}_{2k'+r}$
. Write
$\phi \in {\mathcal S}_{2k'+r}$
. Write
![]() $\bar {h}=\bar {c}'\bar {e}$
, where
$\bar {h}=\bar {c}'\bar {e}$
, where
![]() $\bar {c}'=\bar {h}\cap \bar {c}$
and
$\bar {c}'=\bar {h}\cap \bar {c}$
and
![]() (so
(so
![]() $\bar {e}\subseteq M$
). As
$\bar {e}\subseteq M$
). As
![]() ${\mathcal A}$
is sufficiently large, choose
${\mathcal A}$
is sufficiently large, choose
![]() $\bar {a}\in {\mathcal A}$
disjoint from
$\bar {a}\in {\mathcal A}$
disjoint from
![]() $\bar {b}\bar {b}'\bar {h}$
and let
$\bar {b}\bar {b}'\bar {h}$
and let
![]() $\bar {a}'\subseteq \bar {a}$
be the subsequence corresponding to
$\bar {a}'\subseteq \bar {a}$
be the subsequence corresponding to
![]() $\bar {c}'$
in
$\bar {c}'$
in
![]() $\bar {c}$
. As
$\bar {c}$
. As
![]() $\bar {e}\bar {a}'$
are from M,
$\bar {e}\bar {a}'$
are from M,
![]() $\bar {b}\sim \bar {b}'$
in M, and as
$\bar {b}\sim \bar {b}'$
in M, and as
![]() $\phi $
is quantifier-free, we have
$\phi $
is quantifier-free, we have
Since
![]() $\bar {c}\sim \bar {a}$
in
$\bar {c}\sim \bar {a}$
in
![]() $N_0$
and
$N_0$
and
![]() $\bar {b}\bar {b}'\bar {e}$
is disjoint from
$\bar {b}\bar {b}'\bar {e}$
is disjoint from
![]() $\bar {c}\bar {a}$
, we conclude
$\bar {c}\bar {a}$
, we conclude
![]() $N\models \phi (\bar {b},\bar {b}',\bar {e},\bar {c}')\leftrightarrow \phi (\bar {b}',\bar {b},\bar {e},\bar {c}')$
, as required.⊣
$N\models \phi (\bar {b},\bar {b}',\bar {e},\bar {c}')\leftrightarrow \phi (\bar {b}',\bar {b},\bar {e},\bar {c}')$
, as required.⊣
Consider the case of an equivalence relation with infinitely many infinite classes from Section 1.1. This was easier than the general non-mutually algebraic case. For an example closer to the general case, consider when M is an equivalence relation with infinitely many infinite classes, as well as infinitely many classes of each finite size. If we proceed as in Section 1.1, each
![]() $M_f$
will be isomorphic to M. In this case, the problem is easily remedied by first passing to an age-preserving
$M_f$
will be isomorphic to M. In this case, the problem is easily remedied by first passing to an age-preserving
![]() $M' \supset M$
in which every class is infinite. In the general case, this may not be possible, but we may find some age-preserving
$M' \supset M$
in which every class is infinite. In the general case, this may not be possible, but we may find some age-preserving
![]() $M' \supset M$
in which every (sufficiently large) maximal finite k-clique cannot be extended further. This is the notion of fullness discussed next. Carrying out the construction from Section 1.1 over this
$M' \supset M$
in which every (sufficiently large) maximal finite k-clique cannot be extended further. This is the notion of fullness discussed next. Carrying out the construction from Section 1.1 over this
![]() $M'$
, we will be able to differentiate the maximal finite k-cliques that come from shrinking some infinite
$M'$
, we will be able to differentiate the maximal finite k-cliques that come from shrinking some infinite
![]() ${\mathcal A}_q$
from
${\mathcal A}_q$
from
![]() $M^*$
with those that were already in
$M^*$
with those that were already in
![]() $M'$
, since only the former will be infinitely extendable.
$M'$
, since only the former will be infinitely extendable.
It is easily seen by Zorn’s Lemma that inside every M, every
![]() $k'$
-clique
$k'$
-clique
![]() ${\mathcal A}$
in M is contained in a maximal
${\mathcal A}$
in M is contained in a maximal
![]() $k'$
-clique
$k'$
-clique
![]() ${\mathcal B}\supseteq {\mathcal A}$
in M. What is less clear is whether a maximal
${\mathcal B}\supseteq {\mathcal A}$
in M. What is less clear is whether a maximal
![]() $k'$
-clique
$k'$
-clique
![]() ${\mathcal A}$
can be extended in some age-preserving extension
${\mathcal A}$
can be extended in some age-preserving extension
![]() $N\supseteq M$
.
$N\supseteq M$
.
Definition 4.13. Fix an
![]() ${\mathcal L}$
-structure M.
${\mathcal L}$
-structure M.
-
1. For
 $k'\le k$
, call a
$k'\le k$
, call a
 $k'$
-clique
$k'$
-clique
 ${\mathcal A}$
in M infinitely extendable if there is some age-preserving
${\mathcal A}$
in M infinitely extendable if there is some age-preserving
 $N\supseteq M$
and an infinite
$N\supseteq M$
and an infinite
 $k'$
-clique
$k'$
-clique
 ${\mathcal C}\supseteq {\mathcal A}$
in N, and call
${\mathcal C}\supseteq {\mathcal A}$
in N, and call
 ${\mathcal A}$
unextendable if it is maximal in every age-preserving
${\mathcal A}$
unextendable if it is maximal in every age-preserving
 $N\supseteq M$
.
$N\supseteq M$
. -
2. M is k-full if, for every
 $k'\le k$
, every sufficiently large, maximal
$k'\le k$
, every sufficiently large, maximal
 $k'$
-clique
$k'$
-clique
 ${\mathcal A}$
in M,
${\mathcal A}$
in M,
 ${\mathcal A}$
is either infinite or unextendable.
${\mathcal A}$
is either infinite or unextendable.
Clearly, if a
![]() $k'$
-clique
$k'$
-clique
![]() ${\mathcal A}$
is not infinitely extendable, then there is an age-preserving
${\mathcal A}$
is not infinitely extendable, then there is an age-preserving
![]() $N\supseteq M$
and an unextendable (finite)
$N\supseteq M$
and an unextendable (finite)
![]() $k'$
-clique
$k'$
-clique
![]() ${\mathcal C}$
in N extending
${\mathcal C}$
in N extending
![]() ${\mathcal A}$
. In fact, we can additionally require that the age-preserving extension be
${\mathcal A}$
. In fact, we can additionally require that the age-preserving extension be
![]() $(\le k)$
-clique-preserving as well.
$(\le k)$
-clique-preserving as well.
Lemma 4.14. Suppose M is a countable
![]() ${\mathcal L}$
-structure, and for some
${\mathcal L}$
-structure, and for some
![]() $k'\le k$
,
$k'\le k$
,
![]() ${\mathcal A}$
is a sufficiently large
${\mathcal A}$
is a sufficiently large
![]() $k'$
-clique in M. Then there is an age-preserving,
$k'$
-clique in M. Then there is an age-preserving,
![]() $(\le k)$
-clique-preserving countable
$(\le k)$
-clique-preserving countable
![]() $N\supseteq M$
and an extension
$N\supseteq M$
and an extension
![]() ${\mathcal C}\supseteq {\mathcal A}$
such that
${\mathcal C}\supseteq {\mathcal A}$
such that
![]() $:$
$:$
-
1. If
 ${\mathcal A}$
is infinitely extendable, then
${\mathcal A}$
is infinitely extendable, then
 ${\mathcal C}$
is infinite
${\mathcal C}$
is infinite
 $;$
and
$;$
and -
2. If
 ${\mathcal A}$
is not infinitely extendable, then
${\mathcal A}$
is not infinitely extendable, then
 ${\mathcal C}$
is unextendable.
${\mathcal C}$
is unextendable.
Proof. In both cases, choose an age-preserving
![]() $N^*\supseteq M$
and a
$N^*\supseteq M$
and a
![]() $k'$
-clique
$k'$
-clique
![]() ${\mathcal C}$
in
${\mathcal C}$
in
![]() $N^*$
extending
$N^*$
extending
![]() ${\mathcal A}$
that is either infinite, or of largest possible finite size. In either case, let N be the substructure of
${\mathcal A}$
that is either infinite, or of largest possible finite size. In either case, let N be the substructure of
![]() $N^*$
with universe
$N^*$
with universe
![]() $M\cup \bigcup {\mathcal C}$
. Then N is also an age-preserving extension of M, and moreover N is a clique extension. Thus, N is a
$M\cup \bigcup {\mathcal C}$
. Then N is also an age-preserving extension of M, and moreover N is a clique extension. Thus, N is a
![]() $(\le k)$
-clique-preserving extension of M by Lemma 4.12.⊣
$(\le k)$
-clique-preserving extension of M by Lemma 4.12.⊣
The following lemma now follows by bookkeeping.
Lemma 4.15. Every countable structure M has a countable, k-full,
![]() $(\le k)$
-clique-preserving, age-preserving extension
$(\le k)$
-clique-preserving, age-preserving extension
![]() $N\supseteq M$
.
$N\supseteq M$
.
Proof. We first claim that given any countable M, there is a countable, age-preserving,
![]() $(\le k)$
-clique-preserving
$(\le k)$
-clique-preserving
![]() $M'\supseteq M$
such that for each
$M'\supseteq M$
such that for each
![]() $1\le k'\le k$
, each of the (countably many) sufficiently large, finite
$1\le k'\le k$
, each of the (countably many) sufficiently large, finite
![]() $k'$
-cliques
$k'$
-cliques
![]() ${\mathcal A}$
in M has an extension
${\mathcal A}$
in M has an extension
![]() ${\mathcal C}\supseteq M'$
that is either infinite or is unextendable. (
${\mathcal C}\supseteq M'$
that is either infinite or is unextendable. (
![]() $M'$
is obtained as union of a countable chain of age-preserving,
$M'$
is obtained as union of a countable chain of age-preserving,
![]() $(\le k)$
-clique-preserving extensions formed by iterating Lemma 4.14 once for each such
$(\le k)$
-clique-preserving extensions formed by iterating Lemma 4.14 once for each such
![]() ${\mathcal A}$
.)
${\mathcal A}$
.)
Now, simply iterate the claim above
![]() $\omega $
times, getting a nested sequence
$\omega $
times, getting a nested sequence
![]() $M=M_0\subseteq M_1\subseteq M_2\subseteq \cdots $
with
$M=M_0\subseteq M_1\subseteq M_2\subseteq \cdots $
with
![]() $M_{n+1}=(M_n)'$
from above. Then
$M_{n+1}=(M_n)'$
from above. Then
![]() $N=\bigcup M_n$
is as desired.⊣
$N=\bigcup M_n$
is as desired.⊣
5 Grid extensions
We now generalize the construction of adding infinitely many new equivalence classes from Case 2 of Section 1.1. Throughout this section, we will work within a finite, relational language
![]() ${\mathcal L}$
with arity bounded by r and we will be considering non-mutually algebraic models that are array-minimal of index k (recall Definition 3.1). These k and r are fixed throughout this section. Thus, e.g., a
${\mathcal L}$
with arity bounded by r and we will be considering non-mutually algebraic models that are array-minimal of index k (recall Definition 3.1). These k and r are fixed throughout this section. Thus, e.g., a
![]() $k'$
-clique
$k'$
-clique
![]() ${\mathcal A}$
will be sufficiently large if
${\mathcal A}$
will be sufficiently large if
![]() $|{\mathcal A}|>2k+r$
.
$|{\mathcal A}|>2k+r$
.
Lemma 5.1. Suppose M is not mutually algebraic, M is array-minimal of index k, and there is no age-preserving
![]() $N\supseteq M$
with
$N\supseteq M$
with
![]() $2^{\aleph _0}$
siblings, and let
$2^{\aleph _0}$
siblings, and let
![]() $p\in \mathrm {Supp}_k(M)$
. Then there is an age-preserving, clique-preserving
$p\in \mathrm {Supp}_k(M)$
. Then there is an age-preserving, clique-preserving
![]() $N\supseteq M$
containing an infinite k-clique
$N\supseteq M$
containing an infinite k-clique
![]() with each
with each
![]() $\bar {a}_\ell $
realizing p.
$\bar {a}_\ell $
realizing p.
Proof. As
![]() $p\in \mathrm {Supp}_k(M)$
, we can use Ramsey’s theorem and compactness to find an elementary extension
$p\in \mathrm {Supp}_k(M)$
, we can use Ramsey’s theorem and compactness to find an elementary extension
![]() $M^*\succeq M$
containing an order-indiscernible over M sequence
$M^*\succeq M$
containing an order-indiscernible over M sequence
![]() $\langle \bar {a}_\ell :\ell \in \omega \rangle $
of realizations of p. This sequence must be totally indiscernible over M, as otherwise Proposition 3.3 would give an age-preserving
$\langle \bar {a}_\ell :\ell \in \omega \rangle $
of realizations of p. This sequence must be totally indiscernible over M, as otherwise Proposition 3.3 would give an age-preserving
![]() $N\supseteq M$
with
$N\supseteq M$
with
![]() $2^{\aleph _0}$
siblings. Take N to be the substructure of
$2^{\aleph _0}$
siblings. Take N to be the substructure of
![]() $M^*$
with universe
$M^*$
with universe
![]() . As
. As
![]() is totally indiscernible over its complement, it is a k-clique by Proposition 4.5. The fact that N is age-preserving and clique-preserving follows by Remark 4.10.⊣
is totally indiscernible over its complement, it is a k-clique by Proposition 4.5. The fact that N is age-preserving and clique-preserving follows by Remark 4.10.⊣
Lemma 5.2. Suppose M is not mutually algebraic, M is array-minimal of index k, and there is no age-preserving
![]() $N\supseteq M$
with
$N\supseteq M$
with
![]() $2^{\aleph _0}$
siblings. Then there is an
$2^{\aleph _0}$
siblings. Then there is an
![]() $R(\bar {x},\bar {y}) \in {\mathcal L}$
, an infinite set
$R(\bar {x},\bar {y}) \in {\mathcal L}$
, an infinite set
![]() , a tuple
, a tuple
![]() $\bar {d}_{q,r}\in M^{\lg (\bar {y})}$
for all
$\bar {d}_{q,r}\in M^{\lg (\bar {y})}$
for all
![]() $q<r \in \mathbb {Q}$
, and an age-preserving, clique-preserving
$q<r \in \mathbb {Q}$
, and an age-preserving, clique-preserving
![]() $N\supseteq M$
with infinite k-cliques
$N\supseteq M$
with infinite k-cliques
![]() from N such that, letting
from N such that, letting
![]() , the following hold.
, the following hold.
-
1.
 $\bigcup {\mathcal A}_q \cap \bigcup {\mathcal A}_r = \emptyset $
for
$\bigcup {\mathcal A}_q \cap \bigcup {\mathcal A}_r = \emptyset $
for
 $q \neq r$
.
$q \neq r$
. -
2. For each
 $q \in \mathbb {Q}$
and
$q \in \mathbb {Q}$
and
 $i \in \omega $
,
$i \in \omega $
,
 $\bar {a}_{q,i}$
is a realization of
$\bar {a}_{q,i}$
is a realization of
 $p_q$
.
$p_q$
. -
3. For each
 $q<r \in \mathbb {Q}$
and
$q<r \in \mathbb {Q}$
and
 $i\in \omega $
,
$i\in \omega $
,
 $N\models R(\bar {a}_{q,i},\bar {d}_{q,r})\wedge \neg R(\bar {a}_{r,i},\bar {d}_{q,r})$
.
$N\models R(\bar {a}_{q,i},\bar {d}_{q,r})\wedge \neg R(\bar {a}_{r,i},\bar {d}_{q,r})$
.
Proof. First fix a sequence
![]() $\langle p_i:i\in \mathbb {Q}\rangle $
of distinct complete k-types over M, each of which support an infinite array. As the types are distinct, for each
$\langle p_i:i\in \mathbb {Q}\rangle $
of distinct complete k-types over M, each of which support an infinite array. As the types are distinct, for each
![]() $i<j<\omega $
there is an
$i<j<\omega $
there is an
![]() $R_{i,j}(\bar {x}, \bar {y}_{i,j}) \in {\mathcal L}$
and
$R_{i,j}(\bar {x}, \bar {y}_{i,j}) \in {\mathcal L}$
and
![]() $\bar {d}_{i,j}$
from M such that
$\bar {d}_{i,j}$
from M such that
![]() $R(\bar {x},\bar {d}_{i,j})$
is in
$R(\bar {x},\bar {d}_{i,j})$
is in
![]() $p_i$
but not in
$p_i$
but not in
![]() $p_j$
. As
$p_j$
. As
![]() ${\mathcal L}$
is finite, by Ramsey’s theorem we can choose a specific
${\mathcal L}$
is finite, by Ramsey’s theorem we can choose a specific
![]() $R(\bar {x},\bar {y})$
and an infinite
$R(\bar {x},\bar {y})$
and an infinite
![]() $I\subseteq \mathbb {Q}$
such that
$I\subseteq \mathbb {Q}$
such that
![]() $R_{i,j}=R$
whenever
$R_{i,j}=R$
whenever
![]() $i<j$
from I. Because of this, Clause (3) follows immediately from Clause (2).
$i<j$
from I. Because of this, Clause (3) follows immediately from Clause (2).
We construct N in
![]() $\omega $
steps, once for each
$\omega $
steps, once for each
![]() $i\in I$
, each time applying Lemma 5.1 to the type
$i\in I$
, each time applying Lemma 5.1 to the type
![]() $p_i$
. Because each of the extensions is clique-preserving, the union of this sequence suffices.⊣
$p_i$
. Because each of the extensions is clique-preserving, the union of this sequence suffices.⊣
Definition 5.3.
-
• Fix
 $R(\bar {x},\bar {y}) \in {\mathcal L}$
. A
$R(\bar {x},\bar {y}) \in {\mathcal L}$
. A
 $(k, R)$
-grid extension over M is an age-preserving
$(k, R)$
-grid extension over M is an age-preserving
 $N \supseteq M$
satisfying the following conditions.
$N \supseteq M$
satisfying the following conditions.-
1.
 .
. -
2. The
 $\bar {a}_{q, i}$
are pairwise disjoint and disjoint from M.
$\bar {a}_{q, i}$
are pairwise disjoint and disjoint from M. -
3. For each
 $q \in \mathbb {Q}$
,
$q \in \mathbb {Q}$
,
 is a k-clique.
is a k-clique. -
4. For all
 $q<r \in \mathbb {Q}$
and
$q<r \in \mathbb {Q}$
and
 $i\in \omega $
,
$i\in \omega $
,
 $N\models R(\bar {a}_{q,i},\bar {d}_{q,r})\wedge \neg R(\bar {a}_{r,i}, \bar {d}_{q,r})$
.
$N\models R(\bar {a}_{q,i},\bar {d}_{q,r})\wedge \neg R(\bar {a}_{r,i}, \bar {d}_{q,r})$
.
-
-
• Let
 $\bar {e}_{q,r} = \bar {d}_{q,r} \backslash (M \cup \bigcup _{q\in \mathbb {Q}}(\bigcup {\mathcal A}_q))$
. Given any order-automorphism
$\bar {e}_{q,r} = \bar {d}_{q,r} \backslash (M \cup \bigcup _{q\in \mathbb {Q}}(\bigcup {\mathcal A}_q))$
. Given any order-automorphism
 $\sigma \in Aut(\mathbb {Q},\le )$
, let
$\sigma \in Aut(\mathbb {Q},\le )$
, let
 $\sigma ^*$
be the bijection on N defined as follows.
$\sigma ^*$
be the bijection on N defined as follows.-
1. For
 $q\in \mathbb {Q}$
,
$q\in \mathbb {Q}$
,
 $\sigma ^*(\bar {a}_{q,i})=\bar {a}_{\sigma (q),i}$
.
$\sigma ^*(\bar {a}_{q,i})=\bar {a}_{\sigma (q),i}$
. -
2. For
 $q<r$
from
$q<r$
from
 $\mathbb {Q}$
,
$\mathbb {Q}$
,
 $\sigma ^*(\bar {e}_{q,r})=\bar {e}_{\sigma (q),\sigma (r)}$
.
$\sigma ^*(\bar {e}_{q,r})=\bar {e}_{\sigma (q),\sigma (r)}$
. -
3.
 $\sigma ^*$
fixes M pointwise.
$\sigma ^*$
fixes M pointwise.
-
-
• An indiscernible
 $(k,R)$
-grid extension is a
$(k,R)$
-grid extension is a
 $(k,R)$
-grid extension
$(k,R)$
-grid extension
 $N\supseteq M$
such that, for every
$N\supseteq M$
such that, for every
 $\sigma \in Aut(\mathbb {Q},\le )$
, the induced
$\sigma \in Aut(\mathbb {Q},\le )$
, the induced
 $\sigma ^*$
is an automorphism of N. We call such
$\sigma ^*$
is an automorphism of N. We call such
 $\sigma ^*$
a standard automorphism of N, and any composition of
$\sigma ^*$
a standard automorphism of N, and any composition of
 $\sigma ^*$
with an element of
$\sigma ^*$
with an element of
 $\Pi _{q \in \mathbb {Q}} Sym({\mathcal A}_q)$
a permuted standard automorphism of N.
$\Pi _{q \in \mathbb {Q}} Sym({\mathcal A}_q)$
a permuted standard automorphism of N.
Proposition 5.4. Suppose M is not mutually algebraic, M is array-minimal of index k, and there is no age-preserving extension
![]() $N\supseteq M$
with
$N\supseteq M$
with
![]() $2^{\aleph _0}$
siblings. Then there is an indiscernible
$2^{\aleph _0}$
siblings. Then there is an indiscernible
![]() $(k, R)$
-grid extension
$(k, R)$
-grid extension
![]() $N \supseteq M$
.
$N \supseteq M$
.
Proof. We proceed by compactness. Expand the language by constant symbols naming every element of M, as well as k-tuples of constant symbols
![]() and
and
![]() $\ell $
-tuples of constant symbols
$\ell $
-tuples of constant symbols
![]() , where
, where
![]() $\ell $
is the length of
$\ell $
is the length of
![]() $\bar {d}_{q,r}$
in Lemma 5.2. Consider the theory
$\bar {d}_{q,r}$
in Lemma 5.2. Consider the theory
![]() $T^*$
in this language:
$T^*$
in this language:
-
1. The elementary diagram of M.
-
2. The
 $\bar {a}_{q,i}$
are pairwise disjoint, and no element from M is in any such tuple.
$\bar {a}_{q,i}$
are pairwise disjoint, and no element from M is in any such tuple. -
3. For
 $q<r \in \mathbb {Q}$
,
$q<r \in \mathbb {Q}$
,
 $R(\bar {a}_{q, 0}, \bar {a}_{r,0}, \bar {d}_{q,r}) \wedge \neg R(\bar {a}_{r, 0}, \bar {a}_{q,0}, \bar {d}_{q,r})$
.
$R(\bar {a}_{q, 0}, \bar {a}_{r,0}, \bar {d}_{q,r}) \wedge \neg R(\bar {a}_{r, 0}, \bar {a}_{q,0}, \bar {d}_{q,r})$
. -
4. Each
 is a k-clique, and is order indiscernible over all the other constants.
is a k-clique, and is order indiscernible over all the other constants. -
5. For every
 $\sigma \in Aut(\mathbb {Q}, \leq )$
, let
$\sigma \in Aut(\mathbb {Q}, \leq )$
, let
 $\sigma ^*$
be the induced self-bijection of
$\sigma ^*$
be the induced self-bijection of
 . Then
. Then
 $\sigma ^*$
is an automorphism.
$\sigma ^*$
is an automorphism.
Models of finite subsets of
![]() $T^*$
are obtained by applying the finite Ramsey theorem to the model from Lemma 5.2. Thus, by compactness, we obtain a model
$T^*$
are obtained by applying the finite Ramsey theorem to the model from Lemma 5.2. Thus, by compactness, we obtain a model
![]() $M^* \models T^*$
. Taking the restriction of
$M^* \models T^*$
. Taking the restriction of
![]() $M^*$
to the constant symbols, and letting N be the reduct to the original language, we are finished.⊣
$M^*$
to the constant symbols, and letting N be the reduct to the original language, we are finished.⊣
Definition 5.5. Let
![]() $N \supset M$
be an indiscernible
$N \supset M$
be an indiscernible
![]() $(k,R)$
-grid extension. For
$(k,R)$
-grid extension. For
![]() $q<r \in \mathbb {Q}$
, let
$q<r \in \mathbb {Q}$
, let
![]() $\bar {e}_{q,r}$
be as in Definition 5.3. By indiscernibility, each
$\bar {e}_{q,r}$
be as in Definition 5.3. By indiscernibility, each
![]() $\bar {e}_{i,j}$
must be the same length.
$\bar {e}_{i,j}$
must be the same length.
Define the rank of
![]() $N \supseteq M$
to be the length of any
$N \supseteq M$
to be the length of any
![]() $\bar {e}_{i,j}$
. It is possible for the rank to be 0.
$\bar {e}_{i,j}$
. It is possible for the rank to be 0.
Example 4. Let M consist of an equivalence relation with infinitely many infinite classes, and let
![]() , where each
, where each
![]() is a new class. Then we may take
is a new class. Then we may take
![]() $\bar {d}_{q,r} = a_{q,0}$
, giving rank 0.
$\bar {d}_{q,r} = a_{q,0}$
, giving rank 0.
Our next example codes equivalence relations in a different language. Take M in a language
![]() $(U,V,R)$
, where
$(U,V,R)$
, where
![]() $U,V$
are unary and R is binary. Let U and V be infinite and partition M, and let R be such that for each
$U,V$
are unary and R is binary. Let U and V be infinite and partition M, and let R be such that for each
![]() $u \in U$
there is a unique
$u \in U$
there is a unique
![]() $v \in V$
such that
$v \in V$
such that
![]() $R(u,v)$
, and for each
$R(u,v)$
, and for each
![]() $v \in V$
there are infinitely
$v \in V$
there are infinitely
![]() $u \in U$
such that
$u \in U$
such that
![]() $R(u,v)$
. Let
$R(u,v)$
. Let
![]() , where each
, where each
![]() $u_{q,i} \in U$
,
$u_{q,i} \in U$
,
![]() $v_q \in V$
, and
$v_q \in V$
, and
![]() $R(u_{q,i}, v_r)$
holds if
$R(u_{q,i}, v_r)$
holds if
![]() $q=r$
. Taking
$q=r$
. Taking
![]() and
and
![]() $\bar {d}_{q,r} = v_q$
gives rank 1. We could not have given this extension rank 0, as
$\bar {d}_{q,r} = v_q$
gives rank 1. We could not have given this extension rank 0, as
![]() is totally indiscernible over M; the
is totally indiscernible over M; the
![]() $v_q$
’s are needed to break them into distinct k-cliques.
$v_q$
’s are needed to break them into distinct k-cliques.
We now show that in an indiscernible
![]() $(k, R)$
-grid extension of minimum rank, each
$(k, R)$
-grid extension of minimum rank, each
![]() ${\mathcal A}_i$
is a maximal k-clique.
${\mathcal A}_i$
is a maximal k-clique.
Definition 5.6. Let
![]() $N \supset M$
be an indiscernible
$N \supset M$
be an indiscernible
![]() $(k, R)$
-grid extension. Two tuples
$(k, R)$
-grid extension. Two tuples
![]() $\bar {a}_1 \subset \bar {a}_{q, i}$
,
$\bar {a}_1 \subset \bar {a}_{q, i}$
,
![]() $\bar {a}_2 \subset \bar {a}_{r, j}$
are associated if the natural bijection between
$\bar {a}_2 \subset \bar {a}_{r, j}$
are associated if the natural bijection between
![]() $\bar {a}_{q,i}$
and
$\bar {a}_{q,i}$
and
![]() $\bar {a}_{r, j}$
maps
$\bar {a}_{r, j}$
maps
![]() $\bar {a}_1$
to
$\bar {a}_1$
to
![]() $\bar {a}_2$
.
$\bar {a}_2$
.
The next lemma is analogous to Lemma 3.9.
Lemma 5.7. Suppose M is not mutually algebraic, M is array-minimal of index k, and
![]() $N \supset M$
is an indiscernible
$N \supset M$
is an indiscernible
![]() $(k, R)$
-grid extension. Suppose
$(k, R)$
-grid extension. Suppose
![]() $\bar {a}_1 \subsetneq \bar {a}_{q, i}, \bar {a}_2 \subsetneq \bar {a}_{r, j}$
are associated. Then
$\bar {a}_1 \subsetneq \bar {a}_{q, i}, \bar {a}_2 \subsetneq \bar {a}_{r, j}$
are associated. Then
![]() $\mathrm {tp}(\bar {a}_1/(N \backslash (\bar {a}_{q,i} \cup \bar {a}_{r,j}))) = \mathrm {tp}(\bar {a}_2/(N \backslash (\bar {a}_{q,i} \cup \bar {a}_{r,j})))$
.
$\mathrm {tp}(\bar {a}_1/(N \backslash (\bar {a}_{q,i} \cup \bar {a}_{r,j}))) = \mathrm {tp}(\bar {a}_2/(N \backslash (\bar {a}_{q,i} \cup \bar {a}_{r,j})))$
.
Proof. We may assume
![]() $q \neq r$
, since otherwise this follows from
$q \neq r$
, since otherwise this follows from
![]() $\bar {a}_{q, i} \sim \bar {a}_{q, j}$
, and for definiteness take
$\bar {a}_{q, i} \sim \bar {a}_{q, j}$
, and for definiteness take
![]() $q < r$
. By indiscernibility, it suffices to prove this assuming
$q < r$
. By indiscernibility, it suffices to prove this assuming
![]() $i = j = 0$
. Let
$i = j = 0$
. Let
![]() .
.
Claim.
![]() $\mathrm {tp}(\bar {a}_1 / N_0) = \mathrm {tp} (\bar {a}_2 / N_0)$
.
$\mathrm {tp}(\bar {a}_1 / N_0) = \mathrm {tp} (\bar {a}_2 / N_0)$
.
Proof of Claim. Each standard automorphism fixes
![]() $N_0$
setwise. Suppose
$N_0$
setwise. Suppose
![]() $\mathrm {tp}(\bar {a}_1 / N_0) \neq \mathrm {tp} (\bar {a}_2 / N_0)$
, as witnessed by
$\mathrm {tp}(\bar {a}_1 / N_0) \neq \mathrm {tp} (\bar {a}_2 / N_0)$
, as witnessed by
![]() $\bar {w}$
. Then for any
$\bar {w}$
. Then for any
![]() $\sigma \in Aut(\mathbb {Q}, \leq )$
, the standard automorphism
$\sigma \in Aut(\mathbb {Q}, \leq )$
, the standard automorphism
![]() $\sigma ^*(\bar {w})$
witnesses that
$\sigma ^*(\bar {w})$
witnesses that
![]() $\mathrm {tp}(\sigma ^*(\bar {a}_1) / N_0) \neq \mathrm {tp} (\sigma ^*(\bar {a}_2) / N_0)$
. But this contradicts that M is array-minimal of index k.◊
$\mathrm {tp}(\sigma ^*(\bar {a}_1) / N_0) \neq \mathrm {tp} (\sigma ^*(\bar {a}_2) / N_0)$
. But this contradicts that M is array-minimal of index k.◊
Now suppose
![]() $\bar {w}$
witnesses that
$\bar {w}$
witnesses that
![]() $\mathrm {tp}(\bar {a}_1/(N \backslash (\bar {a}_{q,0} \cup \bar {a}_{r,0}))) \neq \mathrm {tp}(\bar {a}_2/(N \backslash (\bar {a}_{q,0} \cup \bar {a}_{r,0})))$
. Let
$\mathrm {tp}(\bar {a}_1/(N \backslash (\bar {a}_{q,0} \cup \bar {a}_{r,0}))) \neq \mathrm {tp}(\bar {a}_2/(N \backslash (\bar {a}_{q,0} \cup \bar {a}_{r,0})))$
. Let
![]() $\pi \in \Pi _i Sym({\mathcal A}_i)$
be such that
$\pi \in \Pi _i Sym({\mathcal A}_i)$
be such that
![]() $\pi (\bar {w}) \in N_0$
, and
$\pi (\bar {w}) \in N_0$
, and
![]() $\pi $
fixes
$\pi $
fixes
![]() $\bar {a}_{q, 0}$
and
$\bar {a}_{q, 0}$
and
![]() $\bar {a}_{r, 0}$
. Then
$\bar {a}_{r, 0}$
. Then
![]() $\pi (\bar {w})$
witnesses that
$\pi (\bar {w})$
witnesses that
![]() $\mathrm {tp}(\bar {a}_1 / N_0) \neq \mathrm {tp} (\bar {a}_2 / N_0)$
, contradicting the Claim.⊣
$\mathrm {tp}(\bar {a}_1 / N_0) \neq \mathrm {tp} (\bar {a}_2 / N_0)$
, contradicting the Claim.⊣
Lemma 5.8. Suppose M is not mutually algebraic, M is array-minimal of index k, and
![]() $N \supset M$
is an indiscernible
$N \supset M$
is an indiscernible
![]() $(k, R)$
-grid extension of minimum rank. For a given
$(k, R)$
-grid extension of minimum rank. For a given
![]() $q \in \mathbb {Q}$
and
$q \in \mathbb {Q}$
and
![]() $\bar {h} \in N^k$
,
$\bar {h} \in N^k$
,
![]() $\bar {h} \sim \bar {a}_{q, 0}$
only if
$\bar {h} \sim \bar {a}_{q, 0}$
only if
![]() $\bar {h}$
is a permutation of
$\bar {h}$
is a permutation of
![]() $\bar {a}_{q,i}$
for some i.
$\bar {a}_{q,i}$
for some i.
In particular, for every q,
![]() is a maximal k-clique.
is a maximal k-clique.
Proof. Fix
![]() $q \in \mathbb {Q}$
, and suppose
$q \in \mathbb {Q}$
, and suppose
![]() $\bar {h} \in N^k$
is not a permutation of some
$\bar {h} \in N^k$
is not a permutation of some
![]() $\bar {a}_{q, i}$
. Let
$\bar {a}_{q, i}$
. Let
![]() $N = M\sqcup A \sqcup E$
, where
$N = M\sqcup A \sqcup E$
, where
![]() $A = \bigcup _i(\bigcup {\mathcal A}_i)$
and
$A = \bigcup _i(\bigcup {\mathcal A}_i)$
and
![]() $E = N \backslash (M \cup A)$
. The proof splits into two cases.
$E = N \backslash (M \cup A)$
. The proof splits into two cases.
Case 1:
![]() $\bar {h} \cap E \neq \emptyset $
. Let
$\bar {h} \cap E \neq \emptyset $
. Let
![]() $\bar {e}_{s, t} \subset E$
be such that
$\bar {e}_{s, t} \subset E$
be such that
![]() $\bar {e}^h_{s,t} = \bar {h} \cap \bar {e}_{s,t} \neq \emptyset $
, and let
$\bar {e}^h_{s,t} = \bar {h} \cap \bar {e}_{s,t} \neq \emptyset $
, and let
![]() $\bar {e}^{\prime }_{s,t} = \bar {e}_{s,t} \backslash \bar {e}^h_{s,t}$
. As
$\bar {e}^{\prime }_{s,t} = \bar {e}_{s,t} \backslash \bar {e}^h_{s,t}$
. As
![]() $\bar {h} \sim \bar {a}_{q,0}$
, let
$\bar {h} \sim \bar {a}_{q,0}$
, let
![]() $\bar {a}_{q,0}^h \subset \bar {a}_{q,0}$
correspond to the entries of
$\bar {a}_{q,0}^h \subset \bar {a}_{q,0}$
correspond to the entries of
![]() $\bar {e}^h_{q,0}$
. Let
$\bar {e}^h_{q,0}$
. Let
![]() $\bar {d}_{s,t}$
witness that
$\bar {d}_{s,t}$
witness that
![]() $\bar {c}_{s,0} \not \sim \bar {c}_{t,0}$
, with
$\bar {c}_{s,0} \not \sim \bar {c}_{t,0}$
, with
![]() $\bar {e}_{s,t} \subset \bar {d}_{s,t}$
. Let
$\bar {e}_{s,t} \subset \bar {d}_{s,t}$
. Let
![]() $\bar {d}^*_{s,t}$
be obtained by replacing
$\bar {d}^*_{s,t}$
be obtained by replacing
![]() $\bar {e}_{s,t}$
with
$\bar {e}_{s,t}$
with
![]() $\bar {c}^h_{q,0} \bar {e}^{\prime }_{s,t}$
. Let
$\bar {c}^h_{q,0} \bar {e}^{\prime }_{s,t}$
. Let
![]() $\ell $
be large enough that none of the tuples mentioned so far intersect
$\ell $
be large enough that none of the tuples mentioned so far intersect
![]() $\bar {a}_{s, \ell }$
or
$\bar {a}_{s, \ell }$
or
![]() $\bar {a}_{t, \ell }$
. We will show
$\bar {a}_{t, \ell }$
. We will show
![]() $\bar {d}^*_{s,t}$
still witnesses that
$\bar {d}^*_{s,t}$
still witnesses that
![]() $\bar {c}_{s,\ell } \not \sim \bar {c}_{t, \ell }$
, contradicting the fact that N has minimum rank.
$\bar {c}_{s,\ell } \not \sim \bar {c}_{t, \ell }$
, contradicting the fact that N has minimum rank.
By taking an automorphism replacing
![]() $\bar {a}_{q,0}$
with some
$\bar {a}_{q,0}$
with some
![]() $\bar {a}_{q,i}$
, we may assume
$\bar {a}_{q,i}$
, we may assume
![]() $\bar {d}_{s,t} \cap \bar {a}_{q,0} = \emptyset $
. Let
$\bar {d}_{s,t} \cap \bar {a}_{q,0} = \emptyset $
. Let
![]() $\bar {d}^{\prime }_{s,t} = \bar {d}_{s,t} \backslash \bar {e}_{s,t}$
. Since
$\bar {d}^{\prime }_{s,t} = \bar {d}_{s,t} \backslash \bar {e}_{s,t}$
. Since
![]() $\bar {h} \sim \bar {a}_{q,0}$
,
$\bar {h} \sim \bar {a}_{q,0}$
,
![]() $\mathrm {tp}(\bar {h}/\bar {a}_{s, \ell }\bar {a}_{t, \ell } \bar {e}^{\prime }_{s,t}\bar {d}^{\prime }_{s,t}) = \mathrm {tp}(\bar {a}_{q,0}/\bar {a}_{s, \ell }\bar {a}_{t, \ell } \bar {e}^{\prime }_{s,t}\bar {d}^{\prime }_{s,t})$
. Thus
$\mathrm {tp}(\bar {h}/\bar {a}_{s, \ell }\bar {a}_{t, \ell } \bar {e}^{\prime }_{s,t}\bar {d}^{\prime }_{s,t}) = \mathrm {tp}(\bar {a}_{q,0}/\bar {a}_{s, \ell }\bar {a}_{t, \ell } \bar {e}^{\prime }_{s,t}\bar {d}^{\prime }_{s,t})$
. Thus
![]() $\mathrm {tp}(\bar {e}^h_{s,t}/\bar {a}_{s, \ell }\bar {a}_{t, \ell } \bar {e}^{\prime }_{s,t}\bar {d}^{\prime }_{s,t}) = \mathrm {tp}(\bar {a}^h_{q,0}/\bar {a}_{s, \ell }\bar {a}_{t, \ell } \bar {e}^{\prime }_{s,t}\bar {d}^{\prime }_{s,t})$
, and so
$\mathrm {tp}(\bar {e}^h_{s,t}/\bar {a}_{s, \ell }\bar {a}_{t, \ell } \bar {e}^{\prime }_{s,t}\bar {d}^{\prime }_{s,t}) = \mathrm {tp}(\bar {a}^h_{q,0}/\bar {a}_{s, \ell }\bar {a}_{t, \ell } \bar {e}^{\prime }_{s,t}\bar {d}^{\prime }_{s,t})$
, and so
![]() $\mathrm {tp}(\bar {d}_{s,t}/\bar {a}_{s, \ell }\bar {a}_{t, \ell }) = \mathrm {tp}(\bar {d}^*_{s,t}/\bar {a}_{s, \ell }\bar {a}_{t, \ell })$
.
$\mathrm {tp}(\bar {d}_{s,t}/\bar {a}_{s, \ell }\bar {a}_{t, \ell }) = \mathrm {tp}(\bar {d}^*_{s,t}/\bar {a}_{s, \ell }\bar {a}_{t, \ell })$
.
Case 2:
![]() $\bar {h} \cap E = \emptyset $
. Given an interval
$\bar {h} \cap E = \emptyset $
. Given an interval
![]() $[x, y)$
in
$[x, y)$
in
![]() $\omega $
, we define
$\omega $
, we define
![]() . Choose
. Choose
![]() $\ell _1$
such that
$\ell _1$
such that
![]() $\bar {h} \cap A \subset A \upharpoonright _{[0, \ell _1)}$
. Fix
$\bar {h} \cap A \subset A \upharpoonright _{[0, \ell _1)}$
. Fix
![]() $r> q$
, and let
$r> q$
, and let
![]() $\bar {w}$
witness
$\bar {w}$
witness
![]() $\bar {a}_{q, 0} \not \sim \bar {a}_{r, 0}$
. By permuting each
$\bar {a}_{q, 0} \not \sim \bar {a}_{r, 0}$
. By permuting each
![]() ${\mathcal A}_i$
, we may choose
${\mathcal A}_i$
, we may choose
![]() $\ell _2> \ell _1$
so that
$\ell _2> \ell _1$
so that
![]() $\bar {w} \subset A \upharpoonright _{[\ell _1, \ell _2)}$
. For any
$\bar {w} \subset A \upharpoonright _{[\ell _1, \ell _2)}$
. For any
![]() $\ell \geq \ell _2$
, we have
$\ell \geq \ell _2$
, we have
![]() $\bar {w}$
also witnesses
$\bar {w}$
also witnesses
![]() $\bar {a}_{q, \ell } \not \sim \bar {a}_{r, \ell }$
. Let
$\bar {a}_{q, \ell } \not \sim \bar {a}_{r, \ell }$
. Let
![]() $N_0 = N \backslash (A \upharpoonright _{[0, \ell _1)})$
. We use
$N_0 = N \backslash (A \upharpoonright _{[0, \ell _1)})$
. We use
![]() $\bar {x} \sim _{N_0} \bar {y}$
to mean
$\bar {x} \sim _{N_0} \bar {y}$
to mean
![]() $\bar {x}$
and
$\bar {x}$
and
![]() $\bar {y}$
are exchangeable over
$\bar {y}$
are exchangeable over
![]() $N_0$
, i.e., for any
$N_0$
, i.e., for any
![]() $\bar {z}$
from
$\bar {z}$
from
![]() $N_0$
,
$N_0$
,
![]() $\mathrm {tp}(\bar {x}\bar {y}\bar {z}) = \mathrm {tp}(\bar {y}\bar {x}\bar {z})$
.
$\mathrm {tp}(\bar {x}\bar {y}\bar {z}) = \mathrm {tp}(\bar {y}\bar {x}\bar {z})$
.
Claim.
![]() $\bar {h} \sim _{N_0} \bar {a}_{r, \ell }$
.
$\bar {h} \sim _{N_0} \bar {a}_{r, \ell }$
.
Proof of Claim. As
![]() $h \cap E = \emptyset $
, let
$h \cap E = \emptyset $
, let
![]() $\bar {h} \subset \bar {n} \bar {a}_{t_1, i_1} \dots \bar {a}_{t_j, i_j} = \bar {g}$
, where
$\bar {h} \subset \bar {n} \bar {a}_{t_1, i_1} \dots \bar {a}_{t_j, i_j} = \bar {g}$
, where
![]() $\bar {n} = \bar {h} \cap M$
, each
$\bar {n} = \bar {h} \cap M$
, each
![]() $i < \ell _1$
, and
$i < \ell _1$
, and
![]() $t_1 \leq \dots \leq t_j$
. Let
$t_1 \leq \dots \leq t_j$
. Let
![]() $s_1 \leq \dots \leq s_j < q$
, let
$s_1 \leq \dots \leq s_j < q$
, let
![]() $\bar {g}_2 = \bar {n} \bar {a}_{s_1, i_1} \dots \bar {a}_{s_j, i_j}$
, and let
$\bar {g}_2 = \bar {n} \bar {a}_{s_1, i_1} \dots \bar {a}_{s_j, i_j}$
, and let
![]() $\bar {h}_2 \subset \bar {g}_2$
be associated with
$\bar {h}_2 \subset \bar {g}_2$
be associated with
![]() $\bar {h}$
. By Lemma 5.7, we have
$\bar {h}$
. By Lemma 5.7, we have
![]() $\mathrm {tp}(\bar {h}/N_0) = \mathrm {tp}(\bar {h}_2/N_0)$
. In particular,
$\mathrm {tp}(\bar {h}/N_0) = \mathrm {tp}(\bar {h}_2/N_0)$
. In particular,
![]() $\mathrm {tp}(\bar {h}/\bar {c}_{q, \ell }\bar {c}_{r, \ell }\bar {d}) = \mathrm {tp}(\bar {h}_2/\bar {c}_{q, \ell }\bar {c}_{r, \ell }\bar {d})$
, for all
$\mathrm {tp}(\bar {h}/\bar {c}_{q, \ell }\bar {c}_{r, \ell }\bar {d}) = \mathrm {tp}(\bar {h}_2/\bar {c}_{q, \ell }\bar {c}_{r, \ell }\bar {d})$
, for all
![]() $\bar {d} \subset N_0$
.
$\bar {d} \subset N_0$
.
Thus we have
![]() $\bar {h} \sim _{N_0} \bar {a}_{q, \ell } \iff \bar {h}_2 \sim _{N_0} \bar {a}_{q, \ell }$
, and similarly for
$\bar {h} \sim _{N_0} \bar {a}_{q, \ell } \iff \bar {h}_2 \sim _{N_0} \bar {a}_{q, \ell }$
, and similarly for
![]() $\bar {a}_{r, \ell }$
. By assumption,
$\bar {a}_{r, \ell }$
. By assumption,
![]() $\bar {h} \sim \bar {a}_{q, \ell }$
, so we also have
$\bar {h} \sim \bar {a}_{q, \ell }$
, so we also have
![]() $\bar {h} \sim _{N_0} \bar {a}_{q, \ell }$
. Now let
$\bar {h} \sim _{N_0} \bar {a}_{q, \ell }$
. Now let
![]() $\sigma \in Aut(\mathbb {Q}, \leq )$
be an automorphism with
$\sigma \in Aut(\mathbb {Q}, \leq )$
be an automorphism with
![]() $\sigma (q) = r$
and fixing all
$\sigma (q) = r$
and fixing all
![]() $s \leq s_{j}$
, and let
$s \leq s_{j}$
, and let
![]() $\sigma ^*$
be the corresponding standard automorphism. This shows
$\sigma ^*$
be the corresponding standard automorphism. This shows
![]() $\bar {h}_2 \sim _{N_0} \bar {a}_{r, \ell }$
, and so we also have
$\bar {h}_2 \sim _{N_0} \bar {a}_{r, \ell }$
, and so we also have
![]() $\bar {h} \sim _{N_0} \bar {a}_{r, \ell }$
.◊
$\bar {h} \sim _{N_0} \bar {a}_{r, \ell }$
.◊
We now handle the fact that
![]() $\bar {h}$
might intersect
$\bar {h}$
might intersect
![]() $\bar {w}$
. As we took
$\bar {w}$
. As we took
![]() $\bar {w} \in A \upharpoonright _{[\ell _1, \ell _2)}$
, and
$\bar {w} \in A \upharpoonright _{[\ell _1, \ell _2)}$
, and
![]() $\bar {h} \cap E = \emptyset $
, we have
$\bar {h} \cap E = \emptyset $
, we have
![]() $\bar {m} = \bar {h} \cap \bar {w} \subset M$
. Let
$\bar {m} = \bar {h} \cap \bar {w} \subset M$
. Let
![]() $\bar {h} = \bar {h}'\bar {m}$
and
$\bar {h} = \bar {h}'\bar {m}$
and
![]() $\bar {w} = \bar {w}'\bar {m}$
. Then
$\bar {w} = \bar {w}'\bar {m}$
. Then
where we have used
![]() $\bar {h} \sim \bar {a}_{q, \ell }$
in the first and third equalities, and
$\bar {h} \sim \bar {a}_{q, \ell }$
in the first and third equalities, and
![]() $\bar {h} \sim _{N_0} \bar {a}_{r, \ell }$
in the second.
$\bar {h} \sim _{N_0} \bar {a}_{r, \ell }$
in the second.
Removing
![]() $\bar {h}'$
from the initial and final expressions, and noting
$\bar {h}'$
from the initial and final expressions, and noting
![]() $\bar {w} = \bar {w}'(\bar {h} \backslash \bar {h}')$
, we contradict that
$\bar {w} = \bar {w}'(\bar {h} \backslash \bar {h}')$
, we contradict that
![]() $\bar {w}$
witnesses
$\bar {w}$
witnesses
![]() $\bar {a}_{q, \ell } \not \sim \bar {a}_{r, \ell }$
.⊣
$\bar {a}_{q, \ell } \not \sim \bar {a}_{r, \ell }$
.⊣
Definition 5.9. Let
![]() $N \supset M$
be an indiscernible
$N \supset M$
be an indiscernible
![]() $(k, R)$
-grid extension. A k-clique
$(k, R)$
-grid extension. A k-clique
![]() is homogeneous if each
is homogeneous if each
![]() $\bar {b}_s\in {\mathcal B}$
can be partitioned into
$\bar {b}_s\in {\mathcal B}$
can be partitioned into
![]() $\bar {n}_s \bar {m}_s$
(with either part of the partition possibly empty) satisfying the following.
$\bar {n}_s \bar {m}_s$
(with either part of the partition possibly empty) satisfying the following.
-
1.
 $\bar {n}_s$
is from
$\bar {n}_s$
is from
 , and
, and
 $\bar {m}_s$
is from M.
$\bar {m}_s$
is from M. -
2. For each
 $1\le t\le k$
, for all
$1\le t\le k$
, for all
 $s,s'\in I$
,
$s,s'\in I$
,
 $(\bar {b}_s)_t\in M$
iff
$(\bar {b}_s)_t\in M$
iff
 $(\bar {b}_{s'})_t\in M$
.
$(\bar {b}_{s'})_t\in M$
. -
3. For all
 $s,s'\in I$
there is some permuted standard automorphism
$s,s'\in I$
there is some permuted standard automorphism
 $\sigma ^*$
such that
$\sigma ^*$
such that
 $\sigma ^*(\bar {n}_s)=\bar {n}_{s'}$
.
$\sigma ^*(\bar {n}_s)=\bar {n}_{s'}$
.
Lemma 5.10. Suppose that M is k-full and that
![]() $N \supset M$
is an indiscernible
$N \supset M$
is an indiscernible
![]() $(k, R)$
-grid extension. There is a constant
$(k, R)$
-grid extension. There is a constant
![]() $C'$
so that if
$C'$
so that if
![]() ${\mathcal B}$
is a maximal k-clique in N that has size at least
${\mathcal B}$
is a maximal k-clique in N that has size at least
![]() $C'$
and is infinitely extendable, then
$C'$
and is infinitely extendable, then
![]() ${\mathcal B}$
is already infinite.
${\mathcal B}$
is already infinite.
Proof. By two applications of the pigeonhole principle, we can compute a
![]() $C'$
so that any k-clique of size
$C'$
so that any k-clique of size
![]() $C'$
contains a homogeneous k-clique
$C'$
contains a homogeneous k-clique
![]() ${\mathcal B}_0$
with
${\mathcal B}_0$
with
![]() $|{\mathcal B}_0| \geq 2$
. The result will follow by infinitely iterating the following claim to show
$|{\mathcal B}_0| \geq 2$
. The result will follow by infinitely iterating the following claim to show
![]() ${\mathcal B}_0$
is infinitely extendable. By Lemma 4.12
${\mathcal B}_0$
is infinitely extendable. By Lemma 4.12
![]() ${\mathcal B}$
will remain a k-clique in the corresponding clique-extension, and so be infinitely extendable by Lemma 4.6.
${\mathcal B}$
will remain a k-clique in the corresponding clique-extension, and so be infinitely extendable by Lemma 4.6.
Claim. Suppose
![]() ${\mathcal B}_0 \subset N$
is a finite, homogeneous, infinitely extendable k-clique of size at least 2. Then there is a proper extension
${\mathcal B}_0 \subset N$
is a finite, homogeneous, infinitely extendable k-clique of size at least 2. Then there is a proper extension
![]() ${\mathcal B}_1\supsetneq {\mathcal B}_0$
that is also homogeneous.
${\mathcal B}_1\supsetneq {\mathcal B}_0$
that is also homogeneous.
Proof of Claim. First, since
![]() is a k-clique in N, the subsequences
is a k-clique in N, the subsequences
![]() form an
form an
![]() $\ell $
-clique in
$\ell $
-clique in
![]() $M'$
, where
$M'$
, where
![]() $\ell =\lg (\bar {m})$
. Because
$\ell =\lg (\bar {m})$
. Because
![]() ${\mathcal B}_0$
is infinitely extendable, so is
${\mathcal B}_0$
is infinitely extendable, so is
![]() . As
. As
![]() $M'$
is
$M'$
is
![]() $\ell $
-full, we can find some
$\ell $
-full, we can find some
![]() $\bar {m}^*$
so that
$\bar {m}^*$
so that
![]() is an
is an
![]() $\ell $
-clique in
$\ell $
-clique in
![]() $M'$
, and thus in N, as
$M'$
, and thus in N, as
![]() $M' \subset N$
is a k-clique-preserving extension. (If
$M' \subset N$
is a k-clique-preserving extension. (If
![]() $\bar {m}_s$
is empty, this may be ignored.)
$\bar {m}_s$
is empty, this may be ignored.)
Choose a permuted standard automorphism
![]() $\pi \in Aut(N)$
such that
$\pi \in Aut(N)$
such that
![]() $\pi $
fixes
$\pi $
fixes
![]() $\bar {n}_0$
and
$\bar {n}_0$
and
![]() $\pi (\bar {n}_1)$
is disjoint from
$\pi (\bar {n}_1)$
is disjoint from
![]() $\bigcup {\mathcal B}_0$
(the existence of
$\bigcup {\mathcal B}_0$
(the existence of
![]() $\pi $
uses the homogeneity of
$\pi $
uses the homogeneity of
![]() ${\mathcal B}_0$
). Let
${\mathcal B}_0$
). Let
![]() $\bar {n}^*:=\pi (\bar {n}_1)$
. We claim that
$\bar {n}^*:=\pi (\bar {n}_1)$
. We claim that
![]() is a homogeneous k-clique. The homogeneity is clear from the construction. We now show
is a homogeneous k-clique. The homogeneity is clear from the construction. We now show
![]() is a k-clique, and that
is a k-clique, and that
![]() is a k-clique will follow by Lemma 4.6.
is a k-clique will follow by Lemma 4.6.
 $$ \begin{align*} \mathrm{tp}(\bar{n}^*\bar{m}^*\bar{n}_0\bar{m}_0/(N \backslash \bar{n}^*\bar{m}^*\bar{n}_0\bar{m}_0)) &= \mathrm{tp}(\bar{n}^*\bar{m}_1\bar{n}_0\bar{m}_0/(N \backslash \bar{n}^*\bar{m}_1\bar{n}_0\bar{m}_0)) \\ &= \mathrm{tp}(\bar{n}_1\bar{m}_1\bar{n}_0\bar{m}_0/(N \backslash \bar{n}_1\bar{m}_1\bar{n}_0\bar{m}_0)) \\ &= \mathrm{tp}(\bar{n}_0\bar{m}_0\bar{n}_1\bar{m}_1/(N \backslash \bar{n}_1\bar{m}_1\bar{n}_0\bar{m}_0)) \\ &= \mathrm{tp}(\bar{n}_0\bar{m}_0\bar{n}^*\bar{m}_1/(N \backslash \bar{n}^*\bar{m}_1\bar{n}_0\bar{m}_0)) \\ &= \mathrm{tp}(\bar{n}_0\bar{m}_0\bar{n}^*\bar{m}^*/(N \backslash \bar{n}^*\bar{m}^*\bar{n}_0\bar{m}_0)). \end{align*} $$
$$ \begin{align*} \mathrm{tp}(\bar{n}^*\bar{m}^*\bar{n}_0\bar{m}_0/(N \backslash \bar{n}^*\bar{m}^*\bar{n}_0\bar{m}_0)) &= \mathrm{tp}(\bar{n}^*\bar{m}_1\bar{n}_0\bar{m}_0/(N \backslash \bar{n}^*\bar{m}_1\bar{n}_0\bar{m}_0)) \\ &= \mathrm{tp}(\bar{n}_1\bar{m}_1\bar{n}_0\bar{m}_0/(N \backslash \bar{n}_1\bar{m}_1\bar{n}_0\bar{m}_0)) \\ &= \mathrm{tp}(\bar{n}_0\bar{m}_0\bar{n}_1\bar{m}_1/(N \backslash \bar{n}_1\bar{m}_1\bar{n}_0\bar{m}_0)) \\ &= \mathrm{tp}(\bar{n}_0\bar{m}_0\bar{n}^*\bar{m}_1/(N \backslash \bar{n}^*\bar{m}_1\bar{n}_0\bar{m}_0)) \\ &= \mathrm{tp}(\bar{n}_0\bar{m}_0\bar{n}^*\bar{m}^*/(N \backslash \bar{n}^*\bar{m}^*\bar{n}_0\bar{m}_0)). \end{align*} $$
We have used that
![]() is an
is an
![]() $\ell $
-clique in lines 1 and 5, applied
$\ell $
-clique in lines 1 and 5, applied
![]() $\pi ^{-1}$
to get to line 2, used that
$\pi ^{-1}$
to get to line 2, used that
![]() is a k-clique to get to line 3, and applied
is a k-clique to get to line 3, and applied
![]() $\pi $
to get to line 4.◊
$\pi $
to get to line 4.◊
⊣
6 Non-mutually algebraic
 $T$
$T$
Theorem 6.1. If M is a non-mutually algebraic model of T, then there is an age-preserving
![]() $N\supseteq M$
with
$N\supseteq M$
with
![]() $2^{\aleph _0}$
siblings.
$2^{\aleph _0}$
siblings.
Proof. First take an age-preserving
![]() $M" \supseteq M$
that is array-minimal of index k, by Lemma 3.2. Then by Lemma 4.15, let
$M" \supseteq M$
that is array-minimal of index k, by Lemma 3.2. Then by Lemma 4.15, let
![]() $M' \supseteq M"$
be a k-full age-preserving, k-clique-preserving extension. Suppose
$M' \supseteq M"$
be a k-full age-preserving, k-clique-preserving extension. Suppose
![]() $M'$
has no age-preserving extension with
$M'$
has no age-preserving extension with
![]() $2^{\aleph _0}$
siblings, and by Proposition 5.4, let
$2^{\aleph _0}$
siblings, and by Proposition 5.4, let
![]() $N \supseteq M'$
be an indiscernible
$N \supseteq M'$
be an indiscernible
![]() $(k, R)$
-grid extension over
$(k, R)$
-grid extension over
![]() $M'$
, for some
$M'$
, for some
![]() $R \in {\mathcal L}$
, of minimum rank. We will show N has
$R \in {\mathcal L}$
, of minimum rank. We will show N has
![]() $2^{\aleph _0}$
siblings, which is a contradiction.
$2^{\aleph _0}$
siblings, which is a contradiction.
Choose a dense/codense subset
![]() $D \subseteq \mathbb {Q}$
, and let
$D \subseteq \mathbb {Q}$
, and let
![]() $D^c = \mathbb {Q} \backslash D$
. Using the notation of Definition 5.3, let
$D^c = \mathbb {Q} \backslash D$
. Using the notation of Definition 5.3, let
![]() $N_{D^c}$
be the substructure of N with universe
$N_{D^c}$
be the substructure of N with universe
![]() . By the indiscernibility,
. By the indiscernibility,
![]() $N_{D^c}$
is isomorphic to N over
$N_{D^c}$
is isomorphic to N over
![]() $M'$
. Thus, any model
$M'$
. Thus, any model
![]() $N^*$
satisfying
$N^*$
satisfying
![]() $N_{D^c}\subseteq N^* \subseteq N$
is a sibling of N, in fact via embeddings that fix
$N_{D^c}\subseteq N^* \subseteq N$
is a sibling of N, in fact via embeddings that fix
![]() $M'$
pointwise.
$M'$
pointwise.
Let r be the maximum arity of the language, let
![]() $C'$
be from Lemma 5.10, and choose C such that any k-clique of size at least C contains a homogeneous k-clique of size
$C'$
be from Lemma 5.10, and choose C such that any k-clique of size at least C contains a homogeneous k-clique of size
![]() $\max (C', 2k+r)$
. Given an injective
$\max (C', 2k+r)$
. Given an injective
![]() $f \colon D \to \omega \backslash [C]$
, we construct
$f \colon D \to \omega \backslash [C]$
, we construct
![]() $N_f \subset N$
by restricting
$N_f \subset N$
by restricting
![]() ${\mathcal A}_q$
to a subset
${\mathcal A}_q$
to a subset
![]() ${\mathcal A}^*_q$
of size
${\mathcal A}^*_q$
of size
![]() $f(q)$
, for each
$f(q)$
, for each
![]() $q \in D$
. It remains to show the
$q \in D$
. It remains to show the
![]() $N_f$
are pairwise non-isomorphic. The following claim is sufficient, as being an infinitely extendable k-clique of size n is type-definable.
$N_f$
are pairwise non-isomorphic. The following claim is sufficient, as being an infinitely extendable k-clique of size n is type-definable.
Claim. For any
![]() $n\ge C$
,
$n\ge C$
,
![]() $N_f$
has an infinitely extendable maximal k-clique of size n if and only if
$N_f$
has an infinitely extendable maximal k-clique of size n if and only if
![]() $n\in Im(f)$
.⊣
$n\in Im(f)$
.⊣
Proof of Claim.
![]() $(\Leftarrow )$
Let
$(\Leftarrow )$
Let
![]() $q \in \mathbb {Q}$
be such that
$q \in \mathbb {Q}$
be such that
![]() $f(q) = n$
. First, N is visibly a clique extension of
$f(q) = n$
. First, N is visibly a clique extension of
![]() $N_f$
; hence N is
$N_f$
; hence N is
![]() $(\le k)$
-clique-preserving by Lemma 4.12. Thus, as
$(\le k)$
-clique-preserving by Lemma 4.12. Thus, as
![]() ${\mathcal A}_q$
is a maximal k-clique in N by Lemma 5.8,
${\mathcal A}_q$
is a maximal k-clique in N by Lemma 5.8,
![]() ${\mathcal A}^*_q$
is a maximal k-clique in
${\mathcal A}^*_q$
is a maximal k-clique in
![]() $N_f$
. As it is infinitely extendable to
$N_f$
. As it is infinitely extendable to
![]() ${\mathcal A}_q$
, we are finished.
${\mathcal A}_q$
, we are finished.
![]() $(\Rightarrow )$
This will follow immediately from Lemma 6.2.◊
$(\Rightarrow )$
This will follow immediately from Lemma 6.2.◊
⊣
Lemma 6.2. Let
![]() $C \in \omega $
,
$C \in \omega $
,
![]() $D \subset \mathbb {Q}$
,
$D \subset \mathbb {Q}$
,
![]() $N_f$
, and
$N_f$
, and
![]() be as in the proof of Theorem 6.1. If
be as in the proof of Theorem 6.1. If
![]() ${\mathcal B} \subset (N_f)^k$
is a finite infinitely extendable maximal k-clique of size at least C, then there is some
${\mathcal B} \subset (N_f)^k$
is a finite infinitely extendable maximal k-clique of size at least C, then there is some
![]() $q \in D$
such that each element of
$q \in D$
such that each element of
![]() ${\mathcal B}$
is a permutation of some element of
${\mathcal B}$
is a permutation of some element of
![]() ${\mathcal A}^*_q$
.
${\mathcal A}^*_q$
.
Proof. Suppose not. We now work within
![]() $N_f$
. Suppose
$N_f$
. Suppose
![]() $|{\mathcal B}| \geq C$
, let
$|{\mathcal B}| \geq C$
, let
![]() $n=\max (C', 2k+r)$
(where
$n=\max (C', 2k+r)$
(where
![]() $C'$
is from Lemma 5.10 and r is the maximum arity of the language), and let
$C'$
is from Lemma 5.10 and r is the maximum arity of the language), and let
![]() be a homogeneous k-clique. We first prove the conclusion for
be a homogeneous k-clique. We first prove the conclusion for
![]() ${\mathcal B}^-$
. There must be some
${\mathcal B}^-$
. There must be some
![]() $q \in D$
such that
$q \in D$
such that
![]() $\bigcup {\mathcal B}^-$
intersects
$\bigcup {\mathcal B}^-$
intersects
![]() $\bigcup {\mathcal A}^*_q$
; otherwise
$\bigcup {\mathcal A}^*_q$
; otherwise
![]() ${\mathcal B}^-$
would be infinitely extendable by Lemma 5.10. Pick such a q. There is at least one j such that
${\mathcal B}^-$
would be infinitely extendable by Lemma 5.10. Pick such a q. There is at least one j such that
![]() $\bar {b}_0 \cap \bar {a}_{q,j} \neq \emptyset $
, so let
$\bar {b}_0 \cap \bar {a}_{q,j} \neq \emptyset $
, so let
![]() $\bar {c}_0 = \bar {b}_0 \cap \bar {a}_{q,j}$
, and let
$\bar {c}_0 = \bar {b}_0 \cap \bar {a}_{q,j}$
, and let
![]() $\lg (\bar {c}_0) = k' < k$
(this inequality is strict by our assumption that
$\lg (\bar {c}_0) = k' < k$
(this inequality is strict by our assumption that
![]() $\bar {b}_0$
is not a permutation of
$\bar {b}_0$
is not a permutation of
![]() $\bar {a}_{q,j}$
). For each i, let
$\bar {a}_{q,j}$
). For each i, let
![]() $\bar {c}_i$
be the subtuple of
$\bar {c}_i$
be the subtuple of
![]() $\bar {b}_i$
associated with
$\bar {b}_i$
associated with
![]() $\bar {c}_0$
, and let
$\bar {c}_0$
, and let
![]() . By relabeling, we may assume
. By relabeling, we may assume
![]() $\bar {c}_i = \bar {b}_i \cap \bar {a}_{q,i}$
.
$\bar {c}_i = \bar {b}_i \cap \bar {a}_{q,i}$
.
Claim.
![]() ${\mathcal C}$
is a
${\mathcal C}$
is a
![]() $k'$
-clique.
$k'$
-clique.
Proof of Claim. Suppose
![]() $\bar {c}_0 \not \sim \bar {c}_1$
, as witnessed by
$\bar {c}_0 \not \sim \bar {c}_1$
, as witnessed by
![]() $\bar {w}$
, with
$\bar {w}$
, with
![]() $\lg (\bar {w}) \leq r$
. Then
$\lg (\bar {w}) \leq r$
. Then
![]() $\bar {w} \cap (\bar {b}_0 \cup \bar {b}_1) \neq \emptyset $
; otherwise
$\bar {w} \cap (\bar {b}_0 \cup \bar {b}_1) \neq \emptyset $
; otherwise
![]() $\bar {w}$
would witness
$\bar {w}$
would witness
![]() $\bar {b}_0 \not \sim \bar {b}_1$
.
$\bar {b}_0 \not \sim \bar {b}_1$
.
As
![]() ${\mathcal B}^-$
is sufficiently large, by relabeling we may suppose
${\mathcal B}^-$
is sufficiently large, by relabeling we may suppose
![]() $\bar {w}$
does not intersect
$\bar {w}$
does not intersect
![]() $\bar {b}_2 \cup \bar {b}_3$
. Let
$\bar {b}_2 \cup \bar {b}_3$
. Let
![]() $\pi $
be the automorphism swapping
$\pi $
be the automorphism swapping
![]() $\bar {a}_{q,0}$
with
$\bar {a}_{q,0}$
with
![]() $\bar {a}_{q,2}$
and swapping
$\bar {a}_{q,2}$
and swapping
![]() $\bar {a}_{q,1}$
with
$\bar {a}_{q,1}$
with
![]() $\bar {a}_{q,3}$
, while fixing everything else. Then
$\bar {a}_{q,3}$
, while fixing everything else. Then
![]() $\pi (\bar {w})$
witnesses
$\pi (\bar {w})$
witnesses
![]() $\bar {c}_2 \not \sim \bar {c}_3$
, but
$\bar {c}_2 \not \sim \bar {c}_3$
, but
![]() $\pi (\bar {w}) \cap (\bar {b}_2 \cup \bar {b}_3) = \emptyset $
, which is a contradiction.◊
$\pi (\bar {w}) \cap (\bar {b}_2 \cup \bar {b}_3) = \emptyset $
, which is a contradiction.◊
Now work in N, and note that
![]() ${\mathcal C}$
remains a
${\mathcal C}$
remains a
![]() $k'$
-clique in N by Lemma 4.12, since N is a clique extension of
$k'$
-clique in N by Lemma 4.12, since N is a clique extension of
![]() $N_f$
. For each
$N_f$
. For each
![]() $r \in \mathbb {Q}$
, let
$r \in \mathbb {Q}$
, let
![]() $\sigma ^*_r$
be a standard automorphism sending
$\sigma ^*_r$
be a standard automorphism sending
![]() ${\mathcal A}_q$
to
${\mathcal A}_q$
to
![]() ${\mathcal A}_r$
. Each
${\mathcal A}_r$
. Each
![]() $\sigma ^*_r({\mathcal C})$
is a
$\sigma ^*_r({\mathcal C})$
is a
![]() $k'$
-clique that extends to an infinite
$k'$
-clique that extends to an infinite
![]() $k'$
-clique within N. However, for
$k'$
-clique within N. However, for
![]() $r_1 \neq r_2$
,
$r_1 \neq r_2$
,
![]() $\sigma ^*_{r_1}(\bar {c}_0) \not \sim \sigma ^*_{r_2}(\bar {c}_0)$
, since
$\sigma ^*_{r_1}(\bar {c}_0) \not \sim \sigma ^*_{r_2}(\bar {c}_0)$
, since
![]() $\sigma ^*_{r_1}(\bar {a}_0) \not \sim \sigma ^*_{r_2}(\bar {a}_0)$
, so the average types of these infinite extensions are distinct. Thus, by Lemma 4.8, we conclude that
$\sigma ^*_{r_1}(\bar {a}_0) \not \sim \sigma ^*_{r_2}(\bar {a}_0)$
, so the average types of these infinite extensions are distinct. Thus, by Lemma 4.8, we conclude that
![]() $\mathrm {Supp}_{k'}(N)$
is infinite, contradicting that M is array-minimal of index k.
$\mathrm {Supp}_{k'}(N)$
is infinite, contradicting that M is array-minimal of index k.
Given the conclusion for
![]() ${\mathcal B}^-$
, it follows for
${\mathcal B}^-$
, it follows for
![]() ${\mathcal B}$
by Lemma 5.8.⊣
${\mathcal B}$
by Lemma 5.8.⊣
7 Mutually algebraic
 $T$
$T$
7.1 The non-cellular case
In this subsection, we prove that if M is mutually algebraic but non-cellular, then it admits a countable elementary extension with
![]() $2^{\aleph _0}$
siblings.
$2^{\aleph _0}$
siblings.
If
![]() ${\mathcal L}$
is finite relational and M is mutually algebraic, then by Theorem 2.5, there is another finite relational language
${\mathcal L}$
is finite relational and M is mutually algebraic, then by Theorem 2.5, there is another finite relational language
![]() ${\mathcal L}'$
in which every atomic relation is mutually algebraic, and such that
${\mathcal L}'$
in which every atomic relation is mutually algebraic, and such that
![]() ${\mathcal L}'$
is quantifier-free interdefinable with an expansion of
${\mathcal L}'$
is quantifier-free interdefinable with an expansion of
![]() ${\mathcal L}$
naming finitely many constants.
${\mathcal L}$
naming finitely many constants.
Adding finitely many constants to our language changes our sibling count by at most a factor of
![]() ${\aleph _0}$
, and so will not affect this subsection. Adding the constants and switching language to
${\aleph _0}$
, and so will not affect this subsection. Adding the constants and switching language to
![]() ${\mathcal L}'$
as above, we may assume the following.
${\mathcal L}'$
as above, we may assume the following.
For this subsection, we assume M is mutually algebraic in a finite relational language with mutually algebraic atomic relations.
Definition 7.1. Given M in a language with mutually algebraic atomic relations, we may construct a corresponding hypergraph
![]() $G_M$
on the same universe, placing an edge on a tuple
$G_M$
on the same universe, placing an edge on a tuple
![]() $\bar {m}$
if R holds on (some permutation of)
$\bar {m}$
if R holds on (some permutation of)
![]() $\bar {m}$
for some
$\bar {m}$
for some
![]() $R \in {\mathcal L}$
.
$R \in {\mathcal L}$
.
We call
![]() $A\subseteq M$
an MA-connected part if A is a connected part of
$A\subseteq M$
an MA-connected part if A is a connected part of
![]() $G_M$
.
$G_M$
.
Equivalently, we may use that if
![]() $\delta (x,\bar {y})$
and
$\delta (x,\bar {y})$
and
![]() $\theta (x,\bar {z})$
are quantifier-free mutually algebraic with at least one variable symbol x in common, then
$\theta (x,\bar {z})$
are quantifier-free mutually algebraic with at least one variable symbol x in common, then
![]() $\delta (x,\bar {y})\wedge \theta (x,\bar {z})$
is quantifier-free, mutually algebraic. Then
$\delta (x,\bar {y})\wedge \theta (x,\bar {z})$
is quantifier-free, mutually algebraic. Then
![]() $A\subseteq M$
is an MA-connected part iff, for all
$A\subseteq M$
is an MA-connected part iff, for all
![]() $a,b\in A$
, there are
$a,b\in A$
, there are
![]() and a quantifier-free mutually algebraic
and a quantifier-free mutually algebraic
![]() $\phi (x,y,\bar {z})$
such that
$\phi (x,y,\bar {z})$
such that
![]() $M\models \phi (a,b,c_2,\dots ,c_n)$
.
$M\models \phi (a,b,c_2,\dots ,c_n)$
.
An MA-connected component is a maximal MA-connected part.
Lemma 7.2. The following points follow from the corresponding facts for connected parts of hypergraphs.
-
1. If
 $A,B\subseteq M$
are MA-connected parts and
$A,B\subseteq M$
are MA-connected parts and
 $A\cap B=\emptyset $
, then
$A\cap B=\emptyset $
, then
 $A\cup B$
is an MA-connected part.
$A\cup B$
is an MA-connected part. -
2. Every MA-connected part is contained in a unique MA-connected component.
-
3. If C is an infinite MA-connected part, there is a nested sequence
 $B_0 \subsetneq B_1 \subsetneq \cdots $
such that
$B_0 \subsetneq B_1 \subsetneq \cdots $
such that
 $\cup _i B_i = C$
and each
$\cup _i B_i = C$
and each
 $B_i$
is a finite MA-connected part.
$B_i$
is a finite MA-connected part.
Suppose M and N are siblings. Then
![]() $Age(M) = Age(N)$
and so if M thinks that
$Age(M) = Age(N)$
and so if M thinks that
![]() $\delta (x_1,\dots ,x_n)$
is mutually algebraic, then N also thinks this. Using this fact, we have
$\delta (x_1,\dots ,x_n)$
is mutually algebraic, then N also thinks this. Using this fact, we have
![]() $:$
$:$
Lemma 7.3. Suppose M and N are siblings and
![]() $f:M\rightarrow N$
is an embedding. Then for any MA-connected part
$f:M\rightarrow N$
is an embedding. Then for any MA-connected part
![]() $A\subseteq M$
,
$A\subseteq M$
,
![]() $f(A)$
is an MA-connected part of N. Thus, if
$f(A)$
is an MA-connected part of N. Thus, if
![]() $C\subseteq M$
is an MA-connected component, then
$C\subseteq M$
is an MA-connected component, then
![]() $f(C)$
is contained in an MA-connected component as well.
$f(C)$
is contained in an MA-connected component as well.
Lemma 7.4. Suppose M is mutually algebraic and there is an infinite set
![]() of components such that for each i,
of components such that for each i,
![]() $C_i$
properly embeds into
$C_i$
properly embeds into
![]() $C_{i+1}$
, but there is no embedding of
$C_{i+1}$
, but there is no embedding of
![]() $C_{i+1}$
into
$C_{i+1}$
into
![]() $C_i$
. Then M has
$C_i$
. Then M has
![]() $2^{\aleph _0}$
siblings.
$2^{\aleph _0}$
siblings.
Proof. Call an MA-connected component Z outside the scope if there is no embedding of Z into any
![]() $C_i$
. Let
$C_i$
. Let
![]() . Note that any MA-connected component inside the scope embeds into all but finitely many
. Note that any MA-connected component inside the scope embeds into all but finitely many
![]() $C_i$
. For each infinite
$C_i$
. For each infinite
![]() $S\subseteq \omega $
, let
$S\subseteq \omega $
, let
![]() $N_S$
be the substructure of N with universe
$N_S$
be the substructure of N with universe
![]() .
.
We first argue that each
![]() $N_S$
is a sibling of M. Fix any infinite
$N_S$
is a sibling of M. Fix any infinite
![]() $S\subseteq \omega $
. Enumerate the MA-connected components
$S\subseteq \omega $
. Enumerate the MA-connected components
![]() of M that are within the scope. Inductively define a mapping
of M that are within the scope. Inductively define a mapping
![]() $h:M\rightarrow N_S$
as the union of a chain of mappings
$h:M\rightarrow N_S$
as the union of a chain of mappings
![]() $\langle h_n:n\in \omega \rangle $
as follows. Let
$\langle h_n:n\in \omega \rangle $
as follows. Let
![]() $h_0:Z^*\rightarrow N_S$
be the identity. Assume that
$h_0:Z^*\rightarrow N_S$
be the identity. Assume that
![]() has been defined. Given
has been defined. Given
![]() $Y_j$
, choose some i not already chosen so that
$Y_j$
, choose some i not already chosen so that
![]() $Y_j$
embeds into
$Y_j$
embeds into
![]() $C_i$
, and let
$C_i$
, and let
![]() $h_{j+1}$
extend
$h_{j+1}$
extend
![]() $h_j$
by mapping
$h_j$
by mapping
![]() $Y_j$
into
$Y_j$
into
![]() $C_i$
.
$C_i$
.
To see the
![]() $N_S$
are pairwise non-isomorphic, note that
$N_S$
are pairwise non-isomorphic, note that
![]() $N_S$
contains an MA-connected component isomorphic to
$N_S$
contains an MA-connected component isomorphic to
![]() $C_i$
iff
$C_i$
iff
![]() $i \in S$
. As isomorphisms must map MA-connected components to MA-connected components, we are finished.⊣
$i \in S$
. As isomorphisms must map MA-connected components to MA-connected components, we are finished.⊣
Lemma 7.5. If M contains infinite, pairwise isomorphic MA-connected components
![]() , then M has
, then M has
![]() $2^{\aleph _0}$
siblings.
$2^{\aleph _0}$
siblings.
Proof. We will produce a sibling N of M satisfying the hypotheses of Lemma 7.4, which suffices.
Let
![]() $X \subset \omega $
be infinite/co-infinite. We will produce N by shrinking each
$X \subset \omega $
be infinite/co-infinite. We will produce N by shrinking each
![]() $C_i$
with
$C_i$
with
![]() $i \in X$
. We will have that M embeds into N as we leave an infinite collection of
$i \in X$
. We will have that M embeds into N as we leave an infinite collection of
![]() $C_i$
unaltered.
$C_i$
unaltered.
As
![]() $C_0$
is infinite, by Lemma 7.2 write
$C_0$
is infinite, by Lemma 7.2 write
![]() , where each
, where each
![]() $B_i$
is a finite, MA-connected part and
$B_i$
is a finite, MA-connected part and
![]() $B_i \subsetneq B_{i+1}$
for each i. We now construct
$B_i \subsetneq B_{i+1}$
for each i. We now construct
![]() $N \subset M$
by restricting
$N \subset M$
by restricting
![]() $C_i$
down to an isomorphic copy of
$C_i$
down to an isomorphic copy of
![]() $B_i$
, for each
$B_i$
, for each
![]() $i \in X$
.⊣
$i \in X$
.⊣
Theorem 7.6 [Reference Braunfeld and Laskowski3].
Let
![]() ${\mathcal L}$
be finite relational, and suppose M is a mutually algebraic but non-cellular countable
${\mathcal L}$
be finite relational, and suppose M is a mutually algebraic but non-cellular countable
![]() ${\mathcal L}$
-structure. Then there is some
${\mathcal L}$
-structure. Then there is some
![]() $M^* \succ M$
such that
$M^* \succ M$
such that
![]() $M^*$
contains infinitely many new infinite MA-connected components, pairwise isomorphic over M.
$M^*$
contains infinitely many new infinite MA-connected components, pairwise isomorphic over M.
Furthermore, we may take the universe of
![]() $M^*$
to be the universe of M together with these new components.
$M^*$
to be the universe of M together with these new components.
Proposition 7.7. If M is not cellular then there is an age-preserving extension N with
![]() $2^{\aleph _0}$
siblings. In the case where M is mutually algebraic, N can be chosen to be an elementary extension of M.
$2^{\aleph _0}$
siblings. In the case where M is mutually algebraic, N can be chosen to be an elementary extension of M.
7.2 The cellular case
In this subsection, we will be able to directly consider the siblings of M, rather than of some age-preserving extension.
Example 5. Consider the cellular graph M consisting the disjoint union of infinitely many disconnected edges and an infinite independent set. Here, we may obtain
![]() ${\aleph _0}$
siblings as follows. First, we pass to the subgraph N removing the independent set, which will be a sibling of M. Then, for each
${\aleph _0}$
siblings as follows. First, we pass to the subgraph N removing the independent set, which will be a sibling of M. Then, for each
![]() $i \in \omega $
, we obtain a sibling
$i \in \omega $
, we obtain a sibling
![]() $N_i$
by removing a point from i of the edges.
$N_i$
by removing a point from i of the edges.
Note that in a cellular partition
![]() $($
Definition 2.2
$($
Definition 2.2
![]() $)$
, for a fixed
$)$
, for a fixed
![]() $i \in [n]$
,
$i \in [n]$
,
![]() is a
is a
![]() $k_i$
-clique.
$k_i$
-clique.
Definition 7.8. A cellular partition is separated if for every
![]() $i \in [n]$
, there is no proper subtuple of
$i \in [n]$
, there is no proper subtuple of
![]() $\bar {c}_{i,0}$
such that the set of associated subtuples among
$\bar {c}_{i,0}$
such that the set of associated subtuples among
![]() forms a k-clique.
forms a k-clique.
Given a cellular partition, we may always produce a separated cellular partition by increasing n and splitting apart any offending tuples.
Suppose M is cellular, with cellular partition
![]() . Given some
. Given some
![]() $\bar {c}_{i,j}$
and
$\bar {c}_{i,j}$
and
![]() $S \subseteq [k_i]$
, let
$S \subseteq [k_i]$
, let
![]() $\bar {c}_{i,j}^S = (c_{i,j}^\ell | \ell \in S) \subseteq \bar {c}_{i,j}$
. Then every substructure
$\bar {c}_{i,j}^S = (c_{i,j}^\ell | \ell \in S) \subseteq \bar {c}_{i,j}$
. Then every substructure
![]() $N \subseteq M$
is specified by
$N \subseteq M$
is specified by
![]() $N \cap K$
as well as, for each
$N \cap K$
as well as, for each
![]() $i \in [n]$
and
$i \in [n]$
and
![]() $S \subseteq [k_i]$
, the number of j such that
$S \subseteq [k_i]$
, the number of j such that
![]() $N \cap \bar {c}_{i,j} = \bar {c}_{i,j}^S$
.
$N \cap \bar {c}_{i,j} = \bar {c}_{i,j}^S$
.
Recall that M is finitely partitioned if and only if
![]() $|\bar {c}_{i,j}|=1$
for every i.
$|\bar {c}_{i,j}|=1$
for every i.
Lemma 7.9. If M is cellular and not finitely partitioned, then M has
![]() ${\aleph _0}$
siblings.
${\aleph _0}$
siblings.
Proof. By the discussion above, a cellular structure has at most
![]() ${\aleph _0}$
siblings. Let
${\aleph _0}$
siblings. Let
![]() be a separated cellular partition of M. As M is not finitely partitioned, there is some i such that
be a separated cellular partition of M. As M is not finitely partitioned, there is some i such that
![]() $|\bar {c}_{i,j}|> 1$
. Fix some
$|\bar {c}_{i,j}|> 1$
. Fix some
![]() $\ell \in \omega $
, for each
$\ell \in \omega $
, for each
![]() $i,j$
, let
$i,j$
, let
![]() $c_j$
be the first element of
$c_j$
be the first element of
![]() $\bar {c}_{i,j}$
, and let
$\bar {c}_{i,j}$
, and let
![]() . For any
. For any
![]() $i'$
such that
$i'$
such that
![]() $|\bar {c}_{i',j}| = 1$
and
$|\bar {c}_{i',j}| = 1$
and
![]() is a
is a
![]() $1$
-clique, remove all
$1$
-clique, remove all
![]() $\bar {c}_{i',j}$
, and let
$\bar {c}_{i',j}$
, and let
![]() $M^*_\ell $
be the resulting structure. Note
$M^*_\ell $
be the resulting structure. Note
![]() $M^*_\ell $
is a sibling of M.
$M^*_\ell $
is a sibling of M.
We now show there is no
![]() $m \in M^*_\ell \backslash K$
such that
$m \in M^*_\ell \backslash K$
such that
![]() $m \sim c_j$
for some
$m \sim c_j$
for some
![]() $j \leq \ell $
. Suppose there is, and m is the
$j \leq \ell $
. Suppose there is, and m is the
![]() $k^{th}$
element of
$k^{th}$
element of
![]() $\bar {c}_{i',j'}$
for some
$\bar {c}_{i',j'}$
for some
![]() $i' \in [n]$
and
$i' \in [n]$
and
![]() $j' \in \omega $
. Then
$j' \in \omega $
. Then
![]() $c_j$
will be exchangeable with the
$c_j$
will be exchangeable with the
![]() $k^{th}$
element of
$k^{th}$
element of
![]() $\bar {c}_{i',j"}$
for every
$\bar {c}_{i',j"}$
for every
![]() $j" \in \omega $
, and so these elements will form a
$j" \in \omega $
, and so these elements will form a
![]() $1$
-clique. If
$1$
-clique. If
![]() $|\bar {c}_{i', j'}| = 1$
, this contradicts the construction of
$|\bar {c}_{i', j'}| = 1$
, this contradicts the construction of
![]() $M^*_\ell $
. If
$M^*_\ell $
. If
![]() $|\bar {c}_{i', j'}|>1$
, this contradicts that we started with a separated cellular partition.
$|\bar {c}_{i', j'}|>1$
, this contradicts that we started with a separated cellular partition.
Let
![]() $C_\ell $
be the maximal
$C_\ell $
be the maximal
![]() $1$
-clique in
$1$
-clique in
![]() $M^*_\ell $
containing
$M^*_\ell $
containing
![]() . Then
. Then
![]() by the previous paragraph, so
by the previous paragraph, so
![]() $\ell \leq |C_\ell | \leq |K| +\ell $
. In
$\ell \leq |C_\ell | \leq |K| +\ell $
. In
![]() $M^*_\ell $
, any
$M^*_\ell $
, any
![]() $1$
-clique containing a point outside
$1$
-clique containing a point outside
![]() is either a singleton or infinite, since, as in the previous paragraph, if
is either a singleton or infinite, since, as in the previous paragraph, if
![]() $x \sim y$
where y is the
$x \sim y$
where y is the
![]() $k^{th}$
coordinate of
$k^{th}$
coordinate of
![]() $\bar {c}_{i',j'}$
, then x is exchangeable with the
$\bar {c}_{i',j'}$
, then x is exchangeable with the
![]() $k^{th}$
element of
$k^{th}$
element of
![]() $\bar {c}_{i',j"}$
for every
$\bar {c}_{i',j"}$
for every
![]() $j" \in \omega $
. Thus for
$j" \in \omega $
. Thus for
![]() $\ell> |K|$
,
$\ell> |K|$
,
![]() $C_\ell $
will be the largest maximal finite
$C_\ell $
will be the largest maximal finite
![]() $1$
-clique of
$1$
-clique of
![]() $M^*_\ell $
. By the bounds above on
$M^*_\ell $
. By the bounds above on
![]() $|C_\ell |$
, if
$|C_\ell |$
, if
![]() $\ell '> |K|+\ell $
, then
$\ell '> |K|+\ell $
, then
![]() $|C_{\ell '}|> |C_{\ell }|$
, and so
$|C_{\ell '}|> |C_{\ell }|$
, and so
![]() $M^*_{\ell '} \not \cong M^*_{\ell }$
, since their largest maximal finite
$M^*_{\ell '} \not \cong M^*_{\ell }$
, since their largest maximal finite
![]() $1$
-cliques have different sizes. Thus, by varying
$1$
-cliques have different sizes. Thus, by varying
![]() $\ell $
, we may produce
$\ell $
, we may produce
![]() ${\aleph _0}$
siblings of M.⊣
${\aleph _0}$
siblings of M.⊣
Lemma 7.10. If M is finitely partitioned, then M has one sibling, namely itself.
Proof. As M is
![]() $\omega $
-categorical, it admits an
$\omega $
-categorical, it admits an
![]() $\omega $
-categorical model-companion
$\omega $
-categorical model-companion
![]() $M^*$
[Reference Saracino15]. Then
$M^*$
[Reference Saracino15]. Then
![]() $M^*$
is a sibling of M, so it suffices to show
$M^*$
is a sibling of M, so it suffices to show
![]() $M^*$
has only one sibling.
$M^*$
has only one sibling.
As being finitely partitioned is a universal property,
![]() $M^*$
is also finitely partitioned, and so admits a cellular partition with
$M^*$
is also finitely partitioned, and so admits a cellular partition with
![]() $K = \text {acl}(\emptyset )$
, and
$K = \text {acl}(\emptyset )$
, and
![]() $|\bar {c}_{i,j}| = 1$
for each
$|\bar {c}_{i,j}| = 1$
for each
![]() $i \in [n]$
, so let
$i \in [n]$
, so let
![]() $c_{i,j}$
be the one element of
$c_{i,j}$
be the one element of
![]() $\bar {c}_{i,j}$
. We may further assume that we have taken n minimal (subject to
$\bar {c}_{i,j}$
. We may further assume that we have taken n minimal (subject to
![]() $|\bar {c}_{i,j}| = 1$
), and thus
$|\bar {c}_{i,j}| = 1$
), and thus
![]() $tp(c_{i,j}/K) \neq tp(c_{i',j}/K)$
for
$tp(c_{i,j}/K) \neq tp(c_{i',j}/K)$
for
![]() $i \neq i'$
.
$i \neq i'$
.
As
![]() $M^*$
is model-complete, every
$M^*$
is model-complete, every
![]() $x \in K$
is algebraic by an existential formula, so any substructure with the same age must contain all of K. The age of
$x \in K$
is algebraic by an existential formula, so any substructure with the same age must contain all of K. The age of
![]() $M^*$
also specifies
$M^*$
also specifies
![]() is infinite for each i, so any substructure with the same age is isomorphic to
is infinite for each i, so any substructure with the same age is isomorphic to
![]() $M^*$
.⊣
$M^*$
.⊣
7.3 The main theorem
Putting together the results of this section, we have our main theorem.
Theorem 7.11. Let T be a universal theory in a finite relational language. Then one of the following holds.
-
1. T is finitely partitioned. Every model of T has one sibling.
-
2. T is cellular. The finitely partitioned models of T have one sibling and the non-finitely partitioned models have
 $\aleph _0$
siblings.
$\aleph _0$
siblings. -
3. T is not cellular. For every non-cellular
 $M \models T$
, there is some
$M \models T$
, there is some
 $N \supseteq M$
such that
$N \supseteq M$
such that
 $N \models T$
and N has
$N \models T$
and N has
 $2^{\aleph _0}$
siblings. Furthermore, if T is mutually algebraic, we may take
$2^{\aleph _0}$
siblings. Furthermore, if T is mutually algebraic, we may take
 $N \succeq M$
.
$N \succeq M$
.
If T admits a structure universal for its age, this immediately gives the following corollary.
Corollary 7.12. Let M be a countable model in a finite relational language that is universal for its age. Then one of the following holds.
-
1. M is finitely partitioned, and has one sibling.
-
2. M is cellular but not finitely partitioned, and has
 $\aleph _0$
siblings.
$\aleph _0$
siblings. -
3. M is not cellular, and has
 $2^{\aleph _0}$
siblings.
$2^{\aleph _0}$
siblings.
A weakening of “finite relational language” is given in the following definition.
Definition 7.13. We say M has finite profile if, for every n, the number of isomorphism types of substructures of size n is finite.
We now show the assumption of a finite relational language in Corollary 7.12 cannot be weakened to finite profile.
Example 6. Let the language consist of one n-ary relation symbol
![]() $R_n$
for each
$R_n$
for each
![]() $n \in \omega $
. Let
$n \in \omega $
. Let
![]() $\bar {x}_n = (x_n^1, \dots , x_n^n)$
. Let
$\bar {x}_n = (x_n^1, \dots , x_n^n)$
. Let
![]() $M = \bigsqcup _{n \in \omega } \bar {x}_n \sqcup \bigsqcup _{n \in \omega } y_n$
, where
$M = \bigsqcup _{n \in \omega } \bar {x}_n \sqcup \bigsqcup _{n \in \omega } y_n$
, where
![]() $R_n(\bar {x})$
holds iff
$R_n(\bar {x})$
holds iff
![]() $\bar {x} = \bar {x}_n$
, and the
$\bar {x} = \bar {x}_n$
, and the
![]() $y_n$
form an independent set.
$y_n$
form an independent set.
M is not
![]() $\omega $
-categorical, as
$\omega $
-categorical, as
![]() $x_n^i$
and
$x_n^i$
and
![]() $x_m^j$
have different (non-quantifier-free) 1-types for
$x_m^j$
have different (non-quantifier-free) 1-types for
![]() $n \neq m$
. For each n, the isomorphism type of n points is determined by which tuples
$n \neq m$
. For each n, the isomorphism type of n points is determined by which tuples
![]() $\bar {x}_i$
for
$\bar {x}_i$
for
![]() $i \leq n$
they contain, and so M has finite profile. That M is universal for its age is clear by inspection.
$i \leq n$
they contain, and so M has finite profile. That M is universal for its age is clear by inspection.
Age-preserving extensions of M can only add further points to the independent set, and so the only sibling of M is itself. As M is not
![]() $\omega $
-categorical, it is not finitely partitioned, nor even cellular.
$\omega $
-categorical, it is not finitely partitioned, nor even cellular.
As noted in [Reference Laflamme, Pouzet, Sauer and Woodrow7], Corollary 7.12 implies the same conclusion with the hypothesis that M is universal for its age replaced with the hypothesis that M is
![]() $\omega $
-categorical, since we may then pass to the model companion of M.
$\omega $
-categorical, since we may then pass to the model companion of M.
We also obtain a positive answer to a question from [Reference Laflamme, Pouzet, Sauer and Woodrow7] as another corollary of our result. The proof simply goes through each case of Theorem 7.11, which immediately implies the corresponding case of the corollary.
Corollary 7.14. For an age
![]() $\mathfrak A$
in a finite relational language, let
$\mathfrak A$
in a finite relational language, let
![]() $(Mod(\mathfrak A), \leq )$
be the countable structures with age
$(Mod(\mathfrak A), \leq )$
be the countable structures with age
![]() $\mathfrak A$
, quasi-ordered by embeddability. Then for every
$\mathfrak A$
, quasi-ordered by embeddability. Then for every
![]() $M \in Mod(\mathfrak A)$
, the number of structures
$M \in Mod(\mathfrak A)$
, the number of structures
![]() $\leq $
-above M is equal to
$\leq $
-above M is equal to
![]() $|Mod(\mathfrak A)|$
.
$|Mod(\mathfrak A)|$
.
8 Open questions
Conjecture 1 (Thomassé [Reference Thomassé16]).
Given a countable structure M in a countable relational language, M has either 1,
![]() ${\aleph _0}$
, or
${\aleph _0}$
, or
![]() $2^{\aleph _0}$
siblings, up to isomorphism.
$2^{\aleph _0}$
siblings, up to isomorphism.
As mentioned in the introduction, Conjecture 1 seems outside the scope of the model-theoretic approach of this paper. However, an interesting special case to consider may be when M is mutually algebraic. After naming finitely many constants, we may decompose M into MA-connected components, which seem easy to analyze. However, the effect of naming the constants is mysterious.
Problem 1. Confirm Conjecture 1 when M is mutually algebraic.
As noted in the introduction, the arguments in this paper bear out the following intuition
![]() $:$
if a universal theory T is non-cellular, then either it is unstable and so has a model encoding
$:$
if a universal theory T is non-cellular, then either it is unstable and so has a model encoding
![]() $(\mathbb {Q}, <)$
, or has a model that in some sense encodes an infinite partition, i.e., a partition with infinitely many infinite parts.
$(\mathbb {Q}, <)$
, or has a model that in some sense encodes an infinite partition, i.e., a partition with infinitely many infinite parts.
Question 1. What is the proper notion of “encodes an infinite partition” to formalize the intuition above?
Even attempting to plausibly refine Conjecture 1 to describe which structures fall into which of the three cases seems difficult, but answering Question 1 may be helpful. We know that there are two reasons for a universal theory to have a model with
![]() $2^{\aleph _0}$
siblings
$2^{\aleph _0}$
siblings
![]() $:$
either there is a model encoding a linear order with
$:$
either there is a model encoding a linear order with
![]() $2^{\aleph _0}$
siblings
$2^{\aleph _0}$
siblings
![]() $($
namely
$($
namely
![]() $(\mathbb {Q}, <))$
or a model “encoding an infinite partition.” Perhaps the same is essentially true at the level of individual models, although we must weaken the requirement of an infinite partition, since an equivalence relation with arbitrarily large finite classes also has
$(\mathbb {Q}, <))$
or a model “encoding an infinite partition.” Perhaps the same is essentially true at the level of individual models, although we must weaken the requirement of an infinite partition, since an equivalence relation with arbitrarily large finite classes also has
![]() $2^{\aleph _0}$
siblings.
$2^{\aleph _0}$
siblings.
Question 2. If a countable relational structure M has
![]() $2^{\aleph _0}$
siblings, must M either encode a linear order with
$2^{\aleph _0}$
siblings, must M either encode a linear order with
![]() $2^{\aleph _0}$
siblings, or either “encode an infinite partition” or “encode a partition with arbitrarily large finite parts” in the sense of Question 1?
$2^{\aleph _0}$
siblings, or either “encode an infinite partition” or “encode a partition with arbitrarily large finite parts” in the sense of Question 1?
From [Reference Laflamme, Pouzet and Woodrow8], we know exactly which countable linear orders have
![]() $2^{\aleph _0}$
siblings
$2^{\aleph _0}$
siblings
![]() $;$
furthermore, the linear orders with
$;$
furthermore, the linear orders with
![]() $2^{\aleph _0}$
siblings seem to either encode infinite partitions or partitions with arbitrarily large finite parts.
$2^{\aleph _0}$
siblings seem to either encode infinite partitions or partitions with arbitrarily large finite parts.
The final section of [Reference Laflamme, Pouzet, Sauer and Woodrow7] and the introduction of [Reference Macpherson, Pouzet and Woodrow14] contain several open problems, some of which we mention below.
A positive answer to the following conjecture would answer Problem 2 of [Reference Macpherson, Pouzet and Woodrow14]. As mentioned there, Lachlan has proven that an age
![]() $\mathfrak A$
has a unique countable model up to elementary equivalence iff
$\mathfrak A$
has a unique countable model up to elementary equivalence iff
![]() $\mathfrak A$
is finitely partitioned [Reference Lachlan6].
$\mathfrak A$
is finitely partitioned [Reference Lachlan6].
Conjecture 2. All cases of Theorem 7.11 can be strengthened to pairwise non-elementarily equivalent siblings. In particular, given an age
![]() $\mathfrak A$
, there are
$\mathfrak A$
, there are
![]() $2^{\aleph _0}$
non-elementarily equivalent countable structures of age
$2^{\aleph _0}$
non-elementarily equivalent countable structures of age
![]() $\mathfrak A$
iff
$\mathfrak A$
iff
![]() $\mathfrak A$
is non-cellular.
$\mathfrak A$
is non-cellular.
The place where our proof falls short of this conjecture is that whether a k-clique is infinitely extendable does not seem to be definable. However, in some cases, considering infinite extendability is unnecessary
![]() $;$
for example, if M has only finitely many 1-types, in particular if M is
$;$
for example, if M has only finitely many 1-types, in particular if M is
![]() ${\aleph _0}$
-categorical, then there is a bound C on the size of k-cliques appearing in M. When constructing
${\aleph _0}$
-categorical, then there is a bound C on the size of k-cliques appearing in M. When constructing
![]() $N_f$
in Theorem 6.1, we may always shrink our k-cliques above C, and distinguish
$N_f$
in Theorem 6.1, we may always shrink our k-cliques above C, and distinguish
![]() $N_f$
from
$N_f$
from
![]() $N_g$
by whether it has a maximal k-clique of some particular size above C. Thus we have proven Conjecture 2 in the case
$N_g$
by whether it has a maximal k-clique of some particular size above C. Thus we have proven Conjecture 2 in the case
![]() $\mathfrak A$
is the age of an
$\mathfrak A$
is the age of an
![]() ${\aleph _0}$
-categorical structure.
${\aleph _0}$
-categorical structure.
Given an age
![]() $\mathfrak A$
, let
$\mathfrak A$
, let
![]() $Mod(\mathfrak A)/{\equiv }$
denote the bi-embeddability classes of countable structures with age
$Mod(\mathfrak A)/{\equiv }$
denote the bi-embeddability classes of countable structures with age
![]() $\mathfrak A$
. Thomassé’s conjecture is concerned with the size of any single
$\mathfrak A$
. Thomassé’s conjecture is concerned with the size of any single
![]() $\equiv $
-class. There are several conjectures regarding the number of
$\equiv $
-class. There are several conjectures regarding the number of
![]() $\equiv $
-classes in [Reference Laflamme, Pouzet, Sauer and Woodrow7], from which we mention the following.
$\equiv $
-classes in [Reference Laflamme, Pouzet, Sauer and Woodrow7], from which we mention the following.
Conjecture 3 [Reference Laflamme, Pouzet, Sauer and Woodrow7].
For an age
![]() $\mathfrak A$
in a finite relational language,
$\mathfrak A$
in a finite relational language,
![]() $|Mod(\mathfrak A)/{\equiv }|$
is finite if and only if
$|Mod(\mathfrak A)/{\equiv }|$
is finite if and only if
![]() $|Mod(\mathfrak A)/{\equiv }| = 1$
if and only if
$|Mod(\mathfrak A)/{\equiv }| = 1$
if and only if
![]() $\mathfrak A$
is cellular.
$\mathfrak A$
is cellular.
If the conjecture above is true, then the only possibilities for
![]() $|Mod(\mathfrak A)/{\equiv }|$
are
$|Mod(\mathfrak A)/{\equiv }|$
are
![]() [Reference Laflamme, Pouzet, Sauer and Woodrow7]. Classifying which ages fall into which case would be a natural next step.
[Reference Laflamme, Pouzet, Sauer and Woodrow7]. Classifying which ages fall into which case would be a natural next step.
For problems involving model-counting in an age, such as in this paper or the problem of determining
![]() $|Mod(\mathfrak A)|$
in [Reference Macpherson, Pouzet and Woodrow14], the dividing lines are preserved under arbitrary expansions by
$|Mod(\mathfrak A)|$
in [Reference Macpherson, Pouzet and Woodrow14], the dividing lines are preserved under arbitrary expansions by
![]() $($
finitely many
$($
finitely many
![]() $)$
unary relations. This is clear after proving that these dividing lines correspond to being finitely partitioned or being cellular. However, if this could be proven as a first step, then the approach taken in this paper could be drastically simplified, since a non-mutually algebraic theory admits a model such that in a unary expansion there is a definable equivalence relation on singletons with infinitely many infinite classes. We then would not have to use grid extensions to mimic the behavior of such an equivalence relation, and would not have to worry about hybrid tuples.
$)$
unary relations. This is clear after proving that these dividing lines correspond to being finitely partitioned or being cellular. However, if this could be proven as a first step, then the approach taken in this paper could be drastically simplified, since a non-mutually algebraic theory admits a model such that in a unary expansion there is a definable equivalence relation on singletons with infinitely many infinite classes. We then would not have to use grid extensions to mimic the behavior of such an equivalence relation, and would not have to worry about hybrid tuples.
Question 3. Let M be a countable structure in a finite relational language, and let
![]() $M^*$
be an expansion by finitely many unary relations. Let
$M^*$
be an expansion by finitely many unary relations. Let
![]() $\mathfrak A$
and
$\mathfrak A$
and
![]() $\mathfrak A^*$
be their respective ages. Can any of the following statements be proven without first classifying the dividing lines?
$\mathfrak A^*$
be their respective ages. Can any of the following statements be proven without first classifying the dividing lines?
-
1. If
 $|Mod(\mathfrak A^*)| = 2^{\aleph _0}$
, then
$|Mod(\mathfrak A^*)| = 2^{\aleph _0}$
, then
 $|Mod(\mathfrak A)|= 2^{\aleph _0}$
.
$|Mod(\mathfrak A)|= 2^{\aleph _0}$
. -
2. If
 $Mod(\mathfrak A^*)$
has a structure with
$Mod(\mathfrak A^*)$
has a structure with
 $2^{\aleph _0}$
siblings, then so does
$2^{\aleph _0}$
siblings, then so does
 $Mod(\mathfrak A)$
.
$Mod(\mathfrak A)$
. -
3. If
 $|Mod(\mathfrak A^*)/{\equiv }|$
is infinite, then so is
$|Mod(\mathfrak A^*)/{\equiv }|$
is infinite, then so is
 $|Mod(\mathfrak A)/{\equiv }|$
.
$|Mod(\mathfrak A)/{\equiv }|$
.
Acknowledgments
The authors are grateful to the anonymous referee for their careful reading and pointing out inaccuracies in a preliminary version of this paper. The second author was partially supported by NSF grant DMS-1855789.