Article contents
Countable structures, Ehrenfeucht strategies, and Wadge reductions
Published online by Cambridge University Press: 12 March 2014
Abstract
For countable structures 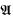 and
and  , let
, let 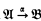 abbreviate the statement that every
abbreviate the statement that every 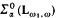 sentence true in
sentence true in 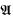 also holds in
also holds in  . One can define a back and forth game between the structures
. One can define a back and forth game between the structures 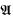 and
and  that determines whether
that determines whether 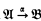 . We verify that if θ is an Lω,ω sentence that is not equivalent to any Lω,ω
. We verify that if θ is an Lω,ω sentence that is not equivalent to any Lω,ω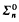 sentence, then there are countably infinite models
sentence, then there are countably infinite models 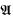 and
and  such that
such that 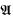 ⊨ θ,
⊨ θ,  ⊨ ¬θ, and
⊨ ¬θ, and 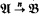 . For countable languages ℒ there is a natural way to view ℒ structúres with universe ω as a topological space, Xℒ. Let [
. For countable languages ℒ there is a natural way to view ℒ structúres with universe ω as a topological space, Xℒ. Let [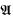 ] = {
] = { ∊ Xℒ∣
∊ Xℒ∣ ≅
≅ 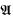 } denote the isomorphism class of
} denote the isomorphism class of 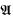 . Let
. Let 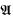 and
and  be countably infinite nonisomorphic ℒ structures, and let C ⊆ ωω be any
be countably infinite nonisomorphic ℒ structures, and let C ⊆ ωω be any 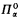 subset. Our main result states that if
subset. Our main result states that if 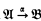 , then there is a continuous function f: ωω → Xℒ with the property that x ∊ C ⇒ f(x) ∊ [
, then there is a continuous function f: ωω → Xℒ with the property that x ∊ C ⇒ f(x) ∊ [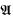 ] and x ∉ C ⇒ f(x) ∊ f(x) ∈ [
] and x ∉ C ⇒ f(x) ∊ f(x) ∈ [ ]. In fact, for α ≤ 3, the continuous function f can be defined from the
]. In fact, for α ≤ 3, the continuous function f can be defined from the  relation.
relation.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1991
References
REFERENCES
- 1
- Cited by


