No CrossRef data available.
Article contents
Corrigendum to: ‘A constructive view on ergodic theorems’
Published online by Cambridge University Press: 12 March 2014
Abstract
Jeremy Avigad kindly pointed out to me that the proof of Theorem 2 in [3] is incomplete. At the very end it assumes that when 
is located, so is 
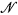. This is not correct. In fact, Avigad explained that the construction in the proof of Theorem 15.3 in [1] can be read as a recursive counterexample to the statement: ‘If 
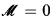, then Anx converges for every x’. As a result the conclusion of Theorem 2 should be that An converges if and only if 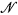is located. Similar changes have to be made in the abstract, Lemma 4, and Theorem 16. Finally, the paragraph on ergodic measure preserving transformations should be removed.
As an unrelated point we would like to mention that in the last two displayed equations of the proof of theorem 1 the term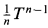 
should be replaced by 
.
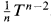- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2006
References
REFERENCES
[1]Avigad, Jeremy and Simic, Ksenija, Fundamental notions of analysis in subsystems of second-order arithmetic, Annals of Pure and Applied Logic, vol. 139 (2006), pp. 138–184.CrossRefGoogle Scholar
[2]Spitters, Bas, Constructive and intuitionistic integration theory and function al analysis, Ph.D. thesis, University of Nijmegen, 2002.Google Scholar
[3]Spitters, Bas, A constructive view on ergodic theorems, this Journal, vol. 71 (2006), no. 2, pp. 611–623.Google Scholar