No CrossRef data available.
Article contents
A correction to Lewis and Langford's Symbolic logic
Published online by Cambridge University Press: 12 March 2014
Extract
The purpose of this note is to call attention to a minor error in Lewis and Langford's Symbolic logic. On page 221, in discussing the Tarski-Łukasiewicz three-valued logic, the authors make the following assertion: “Let T(p) be any proposition, involving only one element, whose analogue holds in the two-valued system; if T(p) does not hold in the Three-valued Calculus, then pC.T(p) and Np.C.T(p) both hold.”
I shall show, by means of a counter-example, that this assertion is not true. Let T(p) be the sentence:
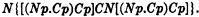
It is then easily verified that T(0) = T(1) = 1, and that T(½) = 0. Thus T(p) holds in the two-valued calculus, but not in the three-valued calculus. On the other hand, pC.T(p) does not hold, since ½.CT(½) = ½C0 = ½; similarly, Np.C.T(p) does not hold, since N½.C.T(½) = ½C0 = ½.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1940
References
1 Lewis, C. I. and Langford, C. H., Symbolic logic, New York and London 1932Google Scholar.


