Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-27T12:24:45.853Z Has data issue: false hasContentIssue false
  • English
  • Français

The consistency of some 4-stratified subsystem of NF including NF3

Published online by Cambridge University Press:  12 March 2014

Maurice Boffa  and
Paolo Casalegno
Maurice Boffa
Affiliation:
Faculty of Sciences, University of Mons, 7000 Mons, Belgium
Paolo Casalegno
Affiliation:
Scuola Normale Superiore, 56100 Pisa, Italy
Get access Rights & Permissions [Opens in a new window]

Extract

As is well known, NF is a first-order theory whose language coincides with that of ZF. The nonlogical axioms of the theory are: Extensionality. (x)(y)[(z)(z ∈ x ↔ z ∈ y) → x = y].

Comprehension. (Ex)(y)(y ∈ x ↔ ψ) for every stratified ψ in which x does not occur free (a formula of NF is said to be stratified if it can be turned into a formula of the simple theory of types by adding type indices (natural numbers ≥ 0) to its variables).

Before stating our result, a few preliminaries are in order. Let T be the simple theory of types. If ψ is a formula of T, we denote by ψ+ the formula obtained from ψ by raising all type indices by 1. T* is the result of adding to T every axiom of the form ψ ↔ ψ+. A formula of T is n-stratified (n > 0) if it does not contain any type index ≥ n. A formula of NF is n-stratified if it can be turned into an n-stratified formula of T by adding type indices to its variables. (In practice, we shall allow ourselves to confuse an n-stratified formula of T with the corresponding n-stratified formula of NF). For n > 0, Tn (resp. 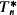) is the subtheory of T (resp. T*) containing only n-stratified formulae. For n > 0, NFn is the subtheory of NF generated by those axioms of NF which are n-stratified. Let 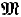= 〈M0, M1,…,=, ∈〉 be a model of T.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 2 , June 1985 , pp. 407 - 411
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, J., Back and forth through infinitary logic, Studies in model theory (Morley, M.D., editor), MAA Studies in Mathematics, vol. 8, Mathematical Association of America, Buffalo, New York, 1973, pp. 5–34.Google Scholar
[2]Boffa, M., The consistency problem for NF, this Journal, vol. 42 (1977), pp. 215–220.Google Scholar
[3]Boffa, M., La théorie des types et NF, Bulletin de la Société Mathématique de Belgique, vol. 33 (1981), pp. 21–31.Google Scholar
[4]Boffa, M. and Crabbé, M., Les théorèmes 3-stratifies de NF3, Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences de Paris, Séries A et B, vol. 280 (1975), pp. A1657–A1658.Google Scholar
[5]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1975.Google Scholar
[6]Grišin, V. N., The method of stratification in set theory, Thesis, Academy of Sciences of the USSR, Moscow, 1973. (Russian)Google Scholar
[7]Grišin, V. N., Consistency of a fragment-of Quine's NF system, Soviet Mathematics: Doklady, vol. 10 (1969), pp. 1387–1390.Google Scholar
[8]Specker, E., The axiom of choice in Quine's new foundations for mathematical logic, Proceedings of the National Academy of Sciences of the United States of America, vol. 39 (1953), pp. 972–975.CrossRefGoogle Scholar
[9]Specker, E., Typical ambiguity, Logic, methodology, and philosophy of science (Proceedings of the 1960 international congress; Nagel, E.et al, editors), Stanford University Press, Stanford, California, 1962, pp. 116–124.Google Scholar