Published online by Cambridge University Press: 12 March 2014
The system 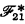 , proposed without a claim as to its consistency in [CLg, §15C], has turned out to entail a consequence which is extremely suspicious. For from the axiom ⊦LH it follows that
, proposed without a claim as to its consistency in [CLg, §15C], has turned out to entail a consequence which is extremely suspicious. For from the axiom ⊦LH it follows that

holds for arbitrary X; hence for X ≡ YH, where Y is a fixed-point combinator, we have

Whether or not this leads to an actual contradiction it would be interesting to know; but, no matter whether it does or not, (2) seems highly counterintuitive.
The aim of this note is to point out that a related system, here called 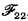 , is demonstrably consistent and sufficient for all practical purposes served by
, is demonstrably consistent and sufficient for all practical purposes served by 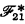 , and at the same time to correct an error in [CLg, §15D2], which was discovered too late to be corrected on the proofs. This
, and at the same time to correct an error in [CLg, §15D2], which was discovered too late to be corrected on the proofs. This 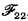 is formed from
is formed from 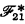 by dropping H from the list of θ's, and hence deleting ⊦LH and (1). The new system does not allow inferential rules to be converted into formulas with the same ease as does
by dropping H from the list of θ's, and hence deleting ⊦LH and (1). The new system does not allow inferential rules to be converted into formulas with the same ease as does 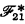 ; but if one is content with stating the results as rules,
; but if one is content with stating the results as rules, 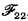 is adequate for all the main results deduced for
is adequate for all the main results deduced for 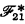 in [CLg, §15C–D].
in [CLg, §15C–D].
This paper was prepared when the author was Visiting Mellon Professor at the University of Pittsburgh.