Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T20:46:08.977Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTING STRENGTH OF STRUCTURES RELATED TO THE FIELD OF REAL NUMBERS

Published online by Cambridge University Press:  21 March 2017

GREGORY IGUSA ,
JULIA F. KNIGHT  and
NOAH DAVID SCHWEBER
GREGORY IGUSA
Affiliation:
MATHEMATICS DEPARTMENT UNIVERSITY OF NOTRE DAME NOTRE DAME, IN, USA and SCHOOL OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY OF WELLINGTON NEW ZEALAND E-mail: [email protected]
JULIA F. KNIGHT
Affiliation:
MATHEMATICS DEPARTMENT UNIVERSITY OF NOTRE DAME NOTRE DAME, IN, USA E-mail: [email protected]
NOAH DAVID SCHWEBER
Affiliation:
MATHEMATICS DEPARTMENT UNIVERSITY OF CALIFORNIA BERKELEY, CA, USA and MATHEMATICS DEPARTMENT UNIVERSITY OF WISCONSIN MADISON, WI, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In [8], the third author defined a reducibility 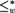$\le _w^{\rm{*}}$ that lets us compare the computing power of structures of any cardinality. In [6], the first two authors showed that the ordered field of reals 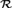${\cal R}$ lies strictly above certain related structures. In the present paper, we show that 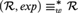$\left( {{\cal R},exp} \right) \equiv _w^{\rm{*}}{\cal R}$ . More generally, for the weak-looking structure 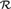${\cal R}$ ℚ consisting of the real numbers with just the ordering and constants naming the rationals, all o-minimal expansions of 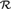${\cal R}$ ℚ are equivalent to 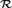${\cal R}$ . Using this, we show that for any analytic function f, 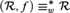$\left( {{\cal R},f} \right) \equiv _w^{\rm{*}}{\cal R}$ . 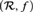(This is so even if $\left( {{\cal R},f} \right)$ is not o-minimal.)

Keywords

03C57 (also, 03C64, 03D45)generic Muchnik reducibilityordered field of realso-minimal theory
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 1 , March 2017 , pp. 137 - 150
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baldwin, J., Friedman, S.-D., Koerwein, M., and Laskowski, C., Three red herrings around Vaught’s Conjecture , Transactions of the American Mathematical Society, vol. 368 (2015), pp. 3673–3694.CrossRefGoogle Scholar
Baldwin, J., Laskowski, M., and Shelah, S., Forcing isomorphism, this Journal, vol. 58 (1993), pp. 1291–1301.Google Scholar
Downey, R., Greenberg, N., and Miller, J., Generic Muchnik reducibility and presentations of fields , Israel Journal of Mathematics, to appear.Google Scholar
Gabrielov, A. M., Projections of semianalytic sets . Functional Analysis and its Applications, vol. 2 (1968), pp. 282–291 (in Russian).Google Scholar
Khovanskii, A., On a class of systems of transcendental equations . Soviet Mathematics Doklady, vol. 22 (1980), pp. 762–765.Google Scholar
Igusa, G. and Knight, J. F., Comparing two versions of the reals using computability, this Journal, vol. 81 (2016), pp. 1115–1123.Google Scholar
Kaplan, I. and Shelah, S., Forcing a countable structure to belong to the ground model , Mathematical Logic Quarterly, to appear.Google Scholar
Knight, J. F., Montalbán, A., and Schweber, N., Computable structures in generic extensions, this Journal, vol. 81 (2016), pp. 814–832.Google Scholar
Knight, J. F., Pillay, A., and Steinhorn, C., Definable sets in ordered structures, II . Transactions of the American Mathematical Society, vol. 295 (1986), pp. 593–605.Google Scholar
Larson, P., Scott processes, preprint.Google Scholar
Macintyre, A. and Marker, D., Degrees of recursively saturated models . Transactions of the American Mathematical Society, vol. 282 (1984), pp. 539–554.Google Scholar
Macintyre, A. and Wilkie, A. J., On the decidability of the real exponential field , Kreiseliana: About and Around Georg Kreisel (Odifreddi, P., editor), A K Peters, Natick, MA, 1996, pp. 441–467.Google Scholar
Pillay, A. and Steinhorn, C., Definable sets in ordered structures, I . Transactions of the American Mathematical Society, vol. 295 (1986), pp. 565–592.CrossRefGoogle Scholar
Tarski, A., A Decision Method for Elementary Algebra and Geometry, University of California Press, Oakland, 1951.CrossRefGoogle Scholar
van den Dries, L., A generalization of the Tarski-Seidenberg Theorem, and some non-definability results . Bulletin of the American Mathematical Society, vol. 15 (1986), pp. 189–193.Google Scholar
van den Dries, L., Tame Topology and o-Minimal Structures, Cambridge University Press, Cambridge, 1998.Google Scholar
Wilkie, A. J., Model completeness results for expansions of the ordered field of real numbers by restricted pfaffian functions and the exponential functions . Journal of the American Mathematical Society, vol. 9 (1996), pp. 1051–1094.CrossRefGoogle Scholar