Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T21:36:53.634Z Has data issue: false hasContentIssue false
  • English
  • Français

Computational logic1

Published online by Cambridge University Press:  12 March 2014

Nathan P. Levin
Nathan P. Levin*
Affiliation:
Los Angeles, California
Get access Rights & Permissions [Opens in a new window]

Extract

We make certain notational conventions. These are referred to as CL (Computational Logic). The relation of interchangeability is introduced as the basic connection between logical formulas. This approach lends perspicuity to the results of sentential calculus. With its technical devices CL is able to rephrase logical theorems in rather succinct manner. Our exposition tries to steer a middle course between informality and strict rigor.

It is felt that the method of CL offers advantages for the teaching of logic. Proofs are algorithmic and resemble those of elementary algebra. All inferences are reversible and practically non-tentative.

Sign is a primitive term of CL. Its denning property is a capacity for entering into binary combination with other signs, or with itself, according to this convention:

x and y are signs if, and only if, (x y) is a sign. Bracketing is looked upon as an operation on signs in terms of which other operations are definable. The practice of some authors in classifying brackets under the heading of symbols, seems to us questionable; for unlike symbols or signs brackets are never used to denote anything. Brackets enter into the composition of signs, not to denote a grouping, but rather to exhibit it, in the manner of a diagram.

An unending list of letters, with or without subscripts,

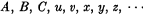
serve to denote arbitrary signs. An arbitrary sign may or may not have other signs as parts. The numeral “2” is used as a constant. Bracketing abbreviation is as follows:

and so on. Outermost brackets will ordinarily be omitted. This kind of bracketing may be termed left-associative. For convenience, these bracketing conventions are crystallized into a rule.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 14 , Issue 3 , September 1949 , pp. 167 - 172
Copyright
Copyright © Association for Symbolic Logic 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The author is indebted to Professor J. C. C. McKinsey for a variety of helpful suggestions and constructive criticisms. The proof of the independence of Postulate (7) is entirely his.

References

2 This system (the axioms are due to Łukasiewicz) is presented in Introduction to mathematical logic, by Alonzo Church, p. 31. It is noteworthy that in the proofs of the axioms of no use was made of (7). We have tried a number of other axiom systems and theorems of sentential calculus and have not yet encountered one requiring (7) for proof. This suggests that, despite the independence of (7), it might be possible to show without using (7) that every tautology is a v-sign.