Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T10:36:25.411Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTABILITY THEORY, NONSTANDARD ANALYSIS, AND THEIR CONNECTIONS

Published online by Cambridge University Press:  23 September 2019

DAG NORMANN  and
SAM SANDERS
DAG NORMANN
Affiliation:
DEPARTMENT OF MATHEMATICS THE UNIVERSITY OF OSLO P.O. BOX 1053, BLINDERN N-0316 OSLO NORWAY E-mail:[email protected]
SAM SANDERS
Affiliation:
DEPARTMENT OF MATHEMATICS TECHNISCHE UNIVERSITÄT DARMSTADT SCHLOSSGARTENSTRASSE 7, D-64289 DARMSTADT GERMANY E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the connections between computability theory and Nonstandard Analysis. In particular, we investigate the two following topics and show that they are intimately related.

(T.1) A basic property of Cantor space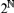$2^ $ is Heine–Borel compactness: for any open covering of 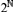$2^ $, there is a finite subcovering. A natural question is: How hard is it to compute such a finite subcovering? We make this precise by analysing the complexity of so-called fan functionals that given any 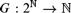$G:2^ \to $, output a finite sequence 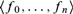$\langle f_0 , \ldots ,f_n \rangle $ in 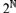$2^ $ such that the neighbourhoods defined from 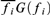$\overline {f_i } G\left( {f_i } \right)$ for 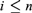$i \le n$ form a covering of 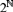$2^ $.

(T.2) A basic property of Cantor space in Nonstandard Analysis is Abraham Robinson’s nonstandard compactness, i.e., that every binary sequence is “infinitely close” to a standard binary sequence. We analyse the strength of this nonstandard compactness property of Cantor space, compared to the other axioms of Nonstandard Analysis and usual mathematics.

Our study of (T.1) yields exotic objects in computability theory, while (T.2) leads to surprising results in Reverse Mathematics. We stress that (T.1) and (T.2) are highly intertwined, i.e., our study is holistic in nature in that results in computability theory yield results in Nonstandard Analysis and vice versa.

Keywords

03B3003D6503F35Nonstandard Analysishigher-order computability theoryhigher-order arithmeticfan functionals
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 4 , December 2019 , pp. 1422 - 1465
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Avigad, J. and Feferman, S., Gödel’s functional (“Dialectica”) interpretation, Handbook of proof theory. Studies in Logic and the Foundations of Mathematics, vol. 137 (1998), pp. 337–405.CrossRefGoogle Scholar
Avigad, J., Dean, E., and Rute, J., Algorithmic randomness, reverse mathematics, and the dominated convergence theorem. Annals of Pure and Applied Logic, vol. 163 (2012), pp. 1854–1864.CrossRefGoogle Scholar
Aczel, P., An introduction to inductive definitions, Handbook of Mathematical Logic (Barwise, J., editor), Studies in Logic and the Foundations of Mathematics, vol. 90, North-Holland, Amsterdam, 1977, pp. 739–782.CrossRefGoogle Scholar
Beeson, M. J., Foundations of Constructive Mathematics, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 6, Springer, Berlin, 1985.CrossRefGoogle Scholar
Berger, U., Uniform heyting arithmetic. Annals of Pure and Applied Logic, vol. 133 (2005), pp. 125–148.CrossRefGoogle Scholar
Bienvenu, L., Patey, L., and Shafer, P., On the logical strengths of partial solutions to mathematical problems. Transactions of the London Mathematical Society, vol. 4 (2017), no. 1, pp. 30–71.CrossRefGoogle Scholar
Blass, A., End extensions, conservative extensions, and the rudin-frolík ordering. Transactions of the American Mathematical Society, vol. 225 (1977), pp. 325–340.Google Scholar
Brouwer, L. E. J., Collected Works, Vol. 1: Philosophy and Foundations of Mathematics (Heyting, A., editor), North-Holland, Amsterdam, 1975.Google Scholar
Borel, E., Sur quelques points de la théorie des fonctions. Annales Scientifiques de l’École Normale Supérieure, vol. 12 (1895), pp. 9–55.CrossRefGoogle Scholar
Cousin, P., Sur les fonctions de n variables complexes. Acta Mathematica, vol. 19 (1895), pp. 1–61.CrossRefGoogle Scholar
Dzhafarov, D. D., Reverse mathematics zoo, http://rmzoo.uconn.edu/.Google Scholar
Escardó, M. and Xu, C., The inconsistency of a Brouwerian continuity principle with the Curry-Howard interpretation, 13th International Conference on Typed Lambda Calculi and Applications (Altenkirch, T., editor), Leibniz International Proceedings in Informatics, vol. 38, Dagstuhl, Saarbrücken, 2015, pp. 153–164.Google Scholar
Ferreira, F. and Gaspar, J., Nonstandardness and the bounded functional interpretation. Annals of Pure and Applied Logic, vol. 166 (2015), no. 6, pp. 701–712.CrossRefGoogle Scholar
Flood, S., Reverse mathematics and a Ramsey-type König’s lemma, this Journal, vol. 77 (2012), no. 4, pp. 1272–1280.Google Scholar
Friedman, H., Some systems of second order arithmetic and their use, Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), vol. 1, Canadian Mathematical Congress, Montreal, 1975, pp. 235–242.Google Scholar
Friedman, H., Systems of second order arithmetic with restricted induction, I & II (abstracts), this Journal, vol. 41 (1976), pp. 557–559.Google Scholar
Friedman, H., Computational nonstandard analysis, FOM mailing list, (Sept. 1st, 2015). https://www.cs.nyu.edu/pipermail/fom/2015-September/018984.html.Google Scholar
Gandy, R., Proof of Mostowski’s conjecture. Bulletin L’Académie Polonaise des Science, Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 8 (1960). (English, with Russian summary).Google Scholar
Gandy, R., General recursive functionals of finite type and hierarchies of functions. Annales de la Faculté des Sciences de Toulouse Clermont-Ferrand No, vol. 35 (1967), pp. 5–24.Google Scholar
Gandy, R. and Hyland, M., Computable and Recursively Countable Functions of Higher Type, Studies in Logic and the Foundations of Mathematics, vol. 87, North-Holland, Amsterdam, 1977, pp. 407–438.Google Scholar
Gordon, E. I., Relatively standard elements in Nelson’s internal set theory. Siberian Mathematical Journal, vol. 30, no. 1, pp. 68–73.CrossRefGoogle Scholar
Hadzihasanovic, A. and van den Berg, B., Nonstandard functional interpretations and categorical models. Notre Dame Journal of Formal Logic, vol. 58 (2017), no. 3, pp. 343–380.CrossRefGoogle Scholar
Harrison, J., Recursive pseudo-well-orderings. Transactions of the American Mathematical Society, vol. 131 (1968), pp. 526–543.CrossRefGoogle Scholar
Hirschfeldt, D. R., Slicing the Truth, Lecture Notes Series. Institute for Mathematical Sciences, vol. 28, World Scientific Publishing, National University of Singapore, 2015.Google Scholar
Hurd, A. E. and Loeb, P. A., An Introduction to Nonstandard Real Analysis, Pure and Applied Mathematics, vol. 118, Academic Press, Orlando, FL, 1985.Google Scholar
Ishihara, H., Reverse mathematics in Bishop’s constructive mathematics. Philosophia Scientiae (Cahier Spécial), vol. 6 (2006), pp. 43–59.CrossRefGoogle Scholar
Keisler, H. J., Nonstandard arithmetic and reverse mathematics. Bulletin of Symbolic Logic, vol. 12 (2006), pp. 100–125.CrossRefGoogle Scholar
Keisler, H. J., Nonstandard arithmetic and recursive comprehension. Annals of Pure and Applied Logic, vol. 161 (2010), no. 8, pp. 1047–1062.CrossRefGoogle Scholar
Kjos-Hanssen, B., Miller, J. S., and Solomon, R., Lowness notions, measure and domination. Journal of the London Mathematical Society (2), vol. 85, (2012), no. 3, pp. 869–888.CrossRefGoogle Scholar
Kleene, S. C., Recursive functionals and quantifiers of finite types. I. Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52.Google Scholar
Kleene, S. C. and Vesley, R. E., The Foundations of Intuitionistic Mathematics, Especially in Relation to Recursive Functions, North–Holland, Amsterdam, 1965.Google Scholar
Kleiner, I., Excursions in the History of Mathematics, Birkhäuser/Springer, New York, 2012.CrossRefGoogle Scholar
Kohlenbach, U., Applied Proof Theory: Proof Interpretations and their Use in Mathematics, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2008.Google Scholar
Kohlenbach, U., Higher order reverse mathematics, Reverse Mathematics 2001 (Simpson, S., editor), Lecture Notes in Mathematics, vol. 21, Peters, A. K., Wellesley, MA, 2005, pp. 281–295.Google Scholar
Kohlenbach, U., Foundational and mathematical uses of higher types, Reflections on the Foundations of Mathematics: Essays in Honor of Solomon Feferman (Sieg, W., Sommer, R., and Talcott, C., editors), Lecture Notes in Mathematics, vol. 15, Peters, A. K., Wellesley, MA, 2002, pp. 92–116.Google Scholar
Kohlenbach, U., On uniform weak König’s lemma. Annals of Pure and Applied Logic, vol. 114 (2002), no. 1–3, pp. 103–116. Commemorative Symposium Dedicated to Anne S. Troelstra (Noordwijkerhout, 1999).Google Scholar
Lindelöf, E., Sur quelques points de la théorie des ensembles. Comptes Rendus, vol. 137 (1903), pp. 697–700.Google Scholar
Longley, J. and Normann, D., Higher-order Computability, Theory and Applications of Computability, Springer, Berlin, 2015.CrossRefGoogle Scholar
Martin-Löf, P., An intuitionistic theory of types: Predicative part, Logic Colloquium ’73 (Rose, H. E. and Shepherdson, J. C., editors), Studies in Logic and the Foundations of Mathematics, vol. 80, North-Holland, Amsterdam, 1975, pp. 73–118.Google Scholar
Montalbán, A., Open questions in reverse mathematics. The Bulletin of Symbolic Logic, vol. 17 (2011), no. 3, pp. 431–454.CrossRefGoogle Scholar
Mummert, C. and Simpson, S. G., Reverse mathematics and ${\rm{\Pi }}_2^1 $ comprehension . The Bulletin of Symbolic Logic, vol. 11 (2005), no. 4, pp. 526–533.CrossRefGoogle Scholar
Nelson, E., Internal set theory: A new approach to nonstandard analysis. Bulletin of the American Mathematical Society, vol. 83 (1977), no. 6, pp. 1165–1198.CrossRefGoogle Scholar
Normann, D., Recursion on the Countable Functionals, Lecture Notes in Mathematics, vol. 811, Springer, Berlin, 1980.CrossRefGoogle Scholar
Normann, D., Functionals of type 3 as realisers of classical theorems in analysis, Proceedings of CiE18, Lecture Notes in Computer Science, Springer, Berlin, 2018, pp. 318–327.CrossRefGoogle Scholar
Normann, D. and Sanders, S., Nonstandard analysis, computability theory, and their connections, preprint, arXiv: https://arxiv.org/abs/1702.06556.Google Scholar
Normann, D. and Sanders, S., The strength of compactness in computability theory and nonstandard analysis. Annals of Pure and Applied Logic, vol. 170 (2019), no. 11, 102710.CrossRefGoogle Scholar
Normann, D. and Sanders, S., On the mathematical and foundational significance of the uncountable. Journal of Mathematical Logic, vol. 19 (2019), no. 1, p. 40.CrossRefGoogle Scholar
Normann, D. and Sanders, S., Representations in measure theory, submitted, 2019, arXiv: https://arxiv.org/abs/1902.02756.Google Scholar
Nuprl, Main website, 2019, http://www.nuprl.org/.Google Scholar
Rahli, V. and Bickford, M., A nominal exploration of intuitionism, Proceedings of the 5th ACM SIGPLAN Conference on Certified Programs and Proofs, Association for Computing Machinery, New York, 2016, pp. 130–141.Google Scholar
Robinson, A., Non-Standard Analysis, North-Holland, Amsterdam, 1966.Google Scholar
Rogers, H., Theory of Recursive Functions and Effective Computability, MIT Press, Cambridge, MA, 1987.Google Scholar
Sacks, G. E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer, Berlin, 1990.CrossRefGoogle Scholar
Sakamoto, N. and Yamazaki, T., Uniform versions of some axioms of second order arithmetic. MLQ Mathematical Logic Quarterly, vol. 50 (2004), no. 6, pp. 587–593.CrossRefGoogle Scholar
Sanders, S., The Gandy-Hyland functional and a computational aspect of nonstandard analysis. Computability, vol. 7 (2018), no. 1, pp. 7–43.CrossRefGoogle Scholar
Sanders, S., Some nonstandard equivalences in reverse mathematics, Sailing Routes in the World of Computation (Manea, F., Miller, R. G., and Nowotka, D., editors), Lecture Notes in Computer Science, vol. 10936, Springer, Berlin, 2018, pp. 365–375.CrossRefGoogle Scholar
Sanders, S., Metastability and higher-order computability, Proceedings of LFCS18, Lecture Notes in Computer Science, vol. 10703, Springer, Berlin, 2018.Google Scholar
Sanders, S., The unreasonable effectiveness of nonstandard analysis, submitted, 2015, available from http://arxiv.org/abs/1508.07434.Google Scholar
Sanders, S., From nonstandard analysis to various flavours of computability theory, Theory and Applications of Models of Computation (Gopal, T. V., Jäger, G., and Steila, S., editors), Lecture Notes in Computer Science, vol. 10185 Springer, Berlin, 2017, pp. 556–570.CrossRefGoogle Scholar
Sanders, S., To be or not to be constructive. Indagationes Mathematicae and the Brouwer Volume L.E.J. Brouwer, Fifty Years Later, 2018, p. 69, https://doi.org/10.1016/j.indag.2017.05.005.Google Scholar
Sanders, S., Refining the taming of the reverse mathematics zoo. Notre Dame Journal of Formal Logic, vol. 59 (2018), no. 4, pp. 579–597.CrossRefGoogle Scholar
Sanders, S. and Yokoyama, K., The Dirac delta function in two settings of reverse mathematics. Archive for Mathematical Logic, vol. 51 (2012), no. 1, pp. 99–121.CrossRefGoogle Scholar
Simpson, S. G. (ed.), Reverse Mathematics 2001, Lecture Notes in Logic, vol. 21, ASL, La Jolla, CA, 2005.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, second ed., Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Simpson, S. G. and Yokoyama, K., A nonstandard counterpart of WWKL. Notre Dame Journal of Formal Logic, vol. 52 (2011), no. 3, pp. 229–243.CrossRefGoogle Scholar
Spector, C., Hyperarithmetical quantifiers. Fundamenta Mathematicae, vol. 48 (1959/60), pp. 313–320.CrossRefGoogle Scholar
Stillwell, J., Reverse Mathematics, Proofs from the Inside Out, Princeton University Press, Princeton, NJ, 2018.Google Scholar
Troelstra, A. S., Metamathematical Investigation of Intuitionistic Arithmetic and Analysis, Lecture Notes in Mathematics, vol. 344, Springer, Berlin, 1973.CrossRefGoogle Scholar
Troelstra, A. S. and van Dalen, D., Constructivism in Mathematics. vol. I, Studies in Logic and the Foundations of Mathematics, vol. 121, North-Holland, Amsterdam, 1988.Google Scholar
van den Berg, B., Briseid, E., and Safarik, P., A functional interpretation for nonstandard arithmetic. Annals of Pure and Applied Logic, vol. 163 (2012), no. 12, pp. 1962–1994.CrossRefGoogle Scholar
van den Berg, B. and Sanders, S., Reverse mathematics and parameter-free transfer. Annals of Pure and Applied Logic, vol. 170 (2019), no. 3, pp. 273–296.CrossRefGoogle Scholar
Vitali, G., Sui gruppi di punti e sulle funzioni di variabili reali.Atti della Accademia delle Scienze di Torino, vol. XLIII, no. 4, (1907), pp. 229–247.Google Scholar
Yu, X. and Simpson, S. G., Measure theory and weak König’s lemma. Archive for Mathematical Logic, vol. 30 (1990), no. 3, pp. 171–180.CrossRefGoogle Scholar