Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2025-01-01T00:00:16.287Z Has data issue: false hasContentIssue false
  • English
  • Français

The complexity of the core model

Published online by Cambridge University Press:  12 March 2014

William J. Mitchell
William J. Mitchell*
Affiliation:
Department of Mathematics, University of Florida, Gainesville, FL 32611., USA. E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

If there is no inner model with a cardinal κ such that ο(κ) = κ++ then the set K ∩ Hω1 is definable over Hω1 by a Δ4 formula, and the set 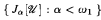of countable initial segments of the core model 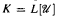is definable over Hω1 by a Π3 formula. We show that if there is an inner model with infinitely many measurable cardinals then there is a model in which 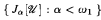is not definable Σ3 by any Σ3 formula, and K ∩ Hω1 is not definable by any boolean combination of Σ3 formulas.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 4 , December 1998 , pp. 1393 - 1398
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Mitchell, William J., The core model for sequences of measures, Mathematics Proceedings of the Cambridge Philosophical Society, vol. 95 (1984), pp. 41—58.CrossRefGoogle Scholar
[2] Mitchell, William J., Σ1 3 absoluteness for sequences of measures, Set theory of the continuum (Judah, H., Just, W., and Woodin, W. Hugh, editors), Springer-Verlag, Berlin, 1992, pp. 311—355.CrossRefGoogle Scholar
[3] Mitchell, William J. and Steel, John R., Fine structure and iteration trees, ASL Lecture Notes in Logic, vol. 3, Springer-Verlag, Berline, 1994.CrossRefGoogle Scholar
[4] Steel, John R., The core model iterahility problem, ASL Lecture Notes in Logic, vol. 8, Springer-Verlag, 1996.CrossRefGoogle Scholar