Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T10:17:45.609Z Has data issue: false hasContentIssue false
  • English
  • Français

The complexity of ODDnA

Published online by Cambridge University Press:  12 March 2014

Richard Beigel ,
William Gasarch ,
Martin Kummer ,
Georgia Martin ,
Timothy Mcnicholl  and
Frank Stephan
Richard Beigel
Affiliation:
Department of Eecs (M/C 154), University of Illinois at Chicago, 851 S. Morgan St. - 1120 Seo, Chicago. IL, 60607-7053U.S.A., E-mail: [email protected]
William Gasarch
Affiliation:
Department of Computer Science, and Institute For Advanced Computing Studies, University of Maryland, College Park. MD 20742, U.S.A., E-mail: [email protected]
Martin Kummer
Affiliation:
Technische Universität Chemnitz-Zwickau, Fakultät Für Informatik, StraΒe Der Nationen 62, 09107 Chemnitz, Germany, Eu, E-mail: [email protected]
Georgia Martin
Affiliation:
12602 Goodhill Road, Wheaton, MD 20906, U.S.A.
Timothy Mcnicholl
Affiliation:
Department of Mathematics, University of Dallas, Irving, TX 75062, U.S.A., E-mail: [email protected]
Frank Stephan
Affiliation:
Mathematisches Institut, Universität Heidelberg, Im Neuenheimer Feld 294, 69120 Heidelberg, GermanyEU, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a fixed set A. the number of queries to A needed in order to decide a set S is a measure of S's complexity. We consider the complexity of certain sets defined in terms of A:

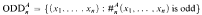
and, for m > 2,

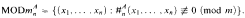
where #nA. (x1….. xn) = A(x1) + A(xn)(We identify 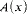with 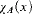, where χA is the characteristic function of A.)

If A is a nonrecursive semirecursive set or if A is a jump, we give tight bounds on the number of queries needed in order to decide ODDnA and MODmnA:

• ODDnA can be decided with n parallel queries to A, but not with n − 1.

• ODDnA can be decided with ⌈log(n + 1)⌉ sequential queries to A but not with ⌈log(n + 1)⌉ − 1.

• MODmnA can be decided with ⌈n/m⌉ + ⌊n/m⌋ parallel queries to A but not with ⌈n/m⌉ + ⌊n/m⌋ − 1.

• MODmnA can be decided with ⌈log(⌈n/m⌉ + ⌊n/m⌋ + 1)⌉ sequential queries to A but not with ⌈log(⌈n/m⌉ + ⌊n/m⌋ + 1)⌉ − 1.

The lower bounds above hold for nonrecursive recursively enumerable sets A as well. (Interestingly, the lower bounds for recursively enumerable sets follow by a general result from the lower bounds for semirecursive sets.)

In particular, every nonzero truth-table degree contains a set A such that ODDnA cannot be decided with n − 1 parallel queries to A. Since every truth-table degree also contains a set B such that ODDnB can be decided with one query to B, a set's query complexity depends more on its structure than on its degree.

For a fixed set A,

Q(n, A) = {S: S can be decided with n sequential queries to A}.

Q∥ (n, A) = {S : S can be decided with n parallel queries to A}.

We show that if A is semirecursive or recursively enumerable, but is not recursive, then these classes form non-collapsing hierarchies:

• Q(0,A) ⊂ Q (1, A) ⊂ Q(2, A) ⊂ …

Q∥ (0, A) ⊂ Q∥ (1, A) ⊂ Q∥ (2, A) ⊂ …

The same is true if A is a jump.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 65 , Issue 1 , March 2000 , pp. 1 - 18
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Bei87a]Beigel, Richard, Functionally supportive sets, Technical Report 87-10, The Johns Hopkins University, Department of Computer Science, 1987.Google Scholar
[Bei87b]Beigel, Richard, Query-limited reducibilities, Ph.D. thesis, Stanford University, 1987, Also available as Report No. STAN-CS-88-1221.Google Scholar
[Bei88]Beigel, Richard, When are k + 1 queries better than k?, Technical Report 88-06, The Johns Hopkins University, Department of Computer Science, 1988.Google Scholar
[BGK96a]Beigel, Richard, Gasarch, William, and Kinber, Efim, Frequency computation and bounded queries, Theoretical Computer Science, vol. 163 (1996), pp. 177–192.CrossRefGoogle Scholar
[BGK+96b]Beigel, Richard, Gasarch, William, Kummer, Martin, Martin, Georgia, McNicholl, Timothy, and Stephan, Frank, On the query complexity of sets, 21st International Symposium on Mathematical Foundations of Computer Science (MFCS '96), Cracow, Poland, 1996.Google Scholar
[BGG093]Beigel, Richard, Gasarch, William I., Gill, John T., and Owings, James C., Terse, superterse, and verbose sets, Information and Computation, vol. 103(1) (03 1993), pp. 68–85.CrossRefGoogle Scholar
[BGH89]Beigel, Richard, Gasarch, William I., and Hay, Louise, Bounded query classes and the difference hierarchy, Archive for Mathematical Logic, vol. 29(2) (12 1989), pp. 69–84.CrossRefGoogle Scholar
[BS90]Boppana, Ravi and Sipser, Michael, The complexity of finite functions, Handbook of theoretical computer science, volume A: Algorithms and complexity (van Leeuwen, Jan, editor), MIT Press and Elsevier, The Netherlands, 1990, pp. 757–804.Google Scholar
[CH89]Cai, Jin-yi and Hemachandra, Lane A., Enumerative counting is hard, Information and Computation, vol. 82(1) (07 1989), pp. 34–44.CrossRefGoogle Scholar
[FSS84]Furst, Merrick, Saxe, James B., and Sipser, Michael, Parity, circuits, and the polynomialtime hierarchy, Mathematical Systems Theory, vol. 17(1) (04 1984), pp. 13–27.CrossRefGoogle Scholar
[Gas91]Gasarch, William, Bounded queries in recursion theory: A survey, Proceedings of the 6th Annual Conference on Structure in Complexity Theory, IEEE Computer Society Press, 06 1991, pp. 62–78.Google Scholar
[GM99]Gasarch, William I. and Martin, Georgia A., Bounded queries in recursion theory, BirkhÄuser, Boston, 1999.CrossRefGoogle Scholar
[GNW95]Goldreich, Oded, Nisan, Noam, and Wigderson, Avi, On Yao's XOR-lemma, Technical Report TR95-050, Electronic Colloquium on Computational Complexity, 1995.Google Scholar
[Has87]HÅstad, Johan, Computational limitations of small-depth circuits, MIT Press, Cambridge, MA, 1987.Google Scholar
[Hay78]Hay, Louise, Convex subsets of 2n and bounded truth-table reducibility, Discrete Mathematics, vol. 21(1) (01 1978), pp. 31–46.CrossRefGoogle Scholar
[Joc89]Jockusch, Carl G., Degrees of functions with no fixed points, Logic, methodology, and philosophy of science VIII (Fenstad, J.E., Frolov, I., Hilpinen, and R., editors), North Holland, 1989, pp. 191–201.Google Scholar
[Joc68]Jockusch, Carl G., Semirecursive sets and positive reducibility, Transactions of the American Mathematical Society, vol. 131 (05 1968), pp. 420–436.CrossRefGoogle Scholar
[JS72]Jockusch, Carl G. Jr., and Soare, Robert I., Π10 classes and degrees of theories, Transactions of the American Matmematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
[Kuc85]Kučera, Antonin, Measure of Π10 classes and complete extensions of PA, Recursion theory week at Oberwolfach, Lecture Notes in Mathematics, vol. 1141, Springer-Verlag, Berlin, 1985, pp. 245–259.CrossRefGoogle Scholar
[Kum92]Kummer, Martin, A proof of Beigel's cardinality conjecture, this Journal, vol. 57(2) (06 1992), pp. 677–681.Google Scholar
[KS94]Kummer, Martin and Stephan, Frank, Effective search problems, Mathematical Logic Quarterly, vol. 40 (1994), pp. 224–236.CrossRefGoogle Scholar
[Lev87]Levin, Leonid A., One way functions and pseudorandom generators, Combinatorica, vol. 7 (1987), pp. 357–363.CrossRefGoogle Scholar
[MM68]Miller, Webb and Martin, Donald A., The degree of hyperimmune sets, Zeitschrift fÜr Mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 159–166.CrossRefGoogle Scholar
[Odi89]Odifreddi, Piergiorgio, Classical recursion theory (Volume I), North-Holland, Amsterdam, 1989.Google Scholar
[Rog67]Rogers, Hartley Jr., Theory of recursive functions and effective computability, McGraw Hill, New York, 1967.Google Scholar
[Smo87]Smolensky, Roman, Algebraic methods in the theory of lower bounds for Boolean circuit complexity, Proceedings of the 19th ACM Symposium on Theory of Computing, 1987, pp. 77–82.Google Scholar
[Soa87]Soare, Robert I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar
[Yao85]Yao, Andrew C., Separating the polynomial-time hierarchy by oracles, Proceedings of the 26th IEEE Symposium on Foundations of Computer Science, 1985, pp. 1–10.Google Scholar