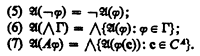Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T02:01:45.312Z Has data issue: false hasContentIssue false
  • English
  • Français

The completeness theorem for infinitary logic

Published online by Cambridge University Press:  12 March 2014

Richard Mansfield
Richard Mansfield*
Affiliation:
Pennsylvania State University, University Park, Pennsylvania 16802
Get access Rights & Permissions [Opens in a new window]

Extract

It will be proven that a set of sentences of infinitary logic is satisfiable iff it is proof theoretically consistent. Since this theorem is known to be false, it must be quickly added that an extended notion of model is being used; truth values may be taken from an arbitrary complete Boolean algebra. We shall give a Henkin style proof of this result which generalizes easily to Boolean valued sets of sentences.

For each infinite candinal number κ the language Lκ is built up from a set of relation symbols together with a constant symbol cα and a variable υα for each α in κ. It contains atomic formulas and is closed under the following rules:

(1) If Γ is a set of formulas of power < κ ∧ Γ is a set of formulas.

(2) If φ is a formula, ¬ φ is also.

(3) If φ is a formula and A Is a subset of κ of power < κ then Aφ is a formula.

∧Γ is meant to be the conjunction of all the formulas in Γ, while Aφ is the universal quantification of all the variables υα for α in A. We let C denote the set of constant symbols in Lκ, the parameter κ must be discovered from the context.

A model is identified with its truth function. Thus a model is a function 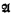mapping the sentences of Lκ into a complete Boolean algebra which satisfies the following conditions:

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 37 , Issue 1 , March 1972 , pp. 31 - 34
Copyright
Copyright © Association for Symbolic Logic 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Halmos, P. R., Lectures on Boolean algebras, Van Nostrand, Princeton, N.J., 1963.Google Scholar
[2]Henkin, L., The completeness of first order function calculus, this Journal, vol. 14 (1949), pp. 159–166.Google Scholar
[3]Karp, C. R., Languages with expressions of infinite length, North-Holland, Amsterdam, 1964.Google Scholar
[4]Keisler, H. J., Infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[5]Royden, H. L., Real analysis, MacMillan, New York, 1963.Google Scholar
[6]Scott, D. and Solovay, R. M., Boolean valued models for set theory, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13, Part II, American Mathematical Society, Providence, R.I. (to appear).Google Scholar