Article contents
COMPLETE LOGICS FOR ELEMENTARY TEAM PROPERTIES
Published online by Cambridge University Press: 01 December 2022
Abstract
In this paper, we introduce a logic based on team semantics, called
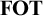 $\mathbf {FOT} $
, whose expressive power is elementary, i.e., coincides with first-order logic both on the level of sentences and (possibly open) formulas, and we also show that a sublogic of
$\mathbf {FOT} $
, whose expressive power is elementary, i.e., coincides with first-order logic both on the level of sentences and (possibly open) formulas, and we also show that a sublogic of
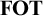 $\mathbf {FOT} $
, called
$\mathbf {FOT} $
, called
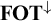 $\mathbf {FOT}^{\downarrow } $
, captures exactly downward closed elementary (or first-order) team properties. We axiomatize completely the logic
$\mathbf {FOT}^{\downarrow } $
, captures exactly downward closed elementary (or first-order) team properties. We axiomatize completely the logic
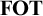 $\mathbf {FOT} $
, and also extend the known partial axiomatization of dependence logic to dependence logic enriched with the logical constants in
$\mathbf {FOT} $
, and also extend the known partial axiomatization of dependence logic to dependence logic enriched with the logical constants in
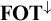 $\mathbf {FOT}^{\downarrow } $
.
$\mathbf {FOT}^{\downarrow } $
.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 3
- Cited by



