Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T19:38:17.265Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPARING THE STRENGTH OF DIAGONALLY NONRECURSIVE FUNCTIONS IN THE ABSENCE OF 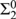${\rm{\Sigma }}_2^0$ INDUCTION

Published online by Cambridge University Press:  22 December 2015

FRANÇOIS G. DORAIS ,
JEFFRY L. HIRST  and
PAUL SHAFER
FRANÇOIS G. DORAIS
Affiliation:
DEPARTMENT OF MATHEMATICS DARTMOUTH COLLEGE HANOVER NH 03755, USAE-mail: [email protected]: http://math.dartmouth.edu/∼dorais/
JEFFRY L. HIRST
Affiliation:
DEPARTMENT OF MATHEMATICAL SCIENCES APPALACHIAN STATE UNIVERSITY BOONE NC 28608, USAE-mail: [email protected]: http://mathsci2.appstate.edu/∼jlh/
PAUL SHAFER
Affiliation:
DEPARTMENT OF MATHEMATICS GHENT UNIVERSITY KRIJGSLAAN 281 S22 B-9000 GHENT, BELGIUME-mail: [email protected]: http://cage.ugent.be/∼pshafer/
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the statement “there is a k such that for every f there is a k-bounded diagonally nonrecursive function relative to f” does not imply weak König’s lemma over 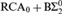${\rm{RC}}{{\rm{A}}_0} + {\rm{B\Sigma }}_2^0$. This answers a question posed by Simpson. A recursion-theoretic consequence is that the classic fact that every k-bounded diagonally nonrecursive function computes a 2-bounded diagonally nonrecursive function may fail in the absence of 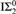${\rm{I\Sigma }}_2^0$.

Keywords

Reverse mathematicsdiagonally nonrecursive functionsWKLDNRnonstandard models of arithmeticgraph coloring
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 4 , December 2015 , pp. 1211 - 1235
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ambos-Spies, Klaus, Kjos-Hanssen, Bjørn, Lempp, Steffen, and Slaman, Theodore A., Comparing DNR and WWKL, this Journal, vol. 69 (2004), no. 4, pp. 1089–1104.Google Scholar
Austen, Jane, Pride and Prejudice, Egerton, T., Whitehall, 1813.Google Scholar
Bean, Dwight R., Effective coloration, this Journal, vol. 41 (1976), no. 2, pp. 469–480.Google Scholar
Chong, C. T., Li, Wei, and Yang, Yue, Nonstandard models in recursion theory and reverse mathematics. Bulletin of Symbolic Logic, vol. 20 (2014), no. 2, pp. 170–200.CrossRefGoogle Scholar
Chong, C. T. and Mourad, K. J., Σndefinable sets without Σninduction. Transactions of the American Mathematical Society, vol. 334 (1992), no. 1, pp. 349–363.Google Scholar
Chong, C. T., Qian, Lei, Slaman, Theodore A., and Yang, Yue, Σ2induction and infinite injury priority arguments, part III: Prompt sets, minimal pairs and Shoenfield’s conjecture. Israel Journal of Mathematics, vol. 121 (2001), pp. 1–28.CrossRefGoogle Scholar
Chong, C. T., Slaman, Theodore A., and Yang, Yue, ${\rm{\Pi }}_1^1$- conservation of combinatorial principles weaker than Ramsey’s theorem for pairs. Advances in Mathematics, vol. 230 (2012), no. 3, pp. 1060–1077.CrossRefGoogle Scholar
Chong, C. T., Slaman, Theodore A., and Yang, Yue, The metamathematics of stable Ramsey’s theorem for pairs. Journal of the American Mathematical Society, vol. 27 (2014), no. 3, pp. 863–892.CrossRefGoogle Scholar
Chong, C. T., Slaman, Theodore A., and Yang, Yue, The inductive strength of Ramsey’s theorem for pairs, 2014, preprint.Google Scholar
Chong, C. T., and Yang, Yue, Σ2induction and infinite injury priority arguments, Part II Tame Σ2coding and the jump operator. Annals of Pure and Applied Logic, vol. 87 (1997), no. 2, pp. 103–116.CrossRefGoogle Scholar
Chong, C. T., and Yang, Yue, Σ2induction and infinite injury priority argument, Part I: Maximal sets and the jump operator, this Journal, vol. 63 (1998), no. 3, pp. 797–814.Google Scholar
Chubb, Jennifer, Hirst, Jeffry L., and McNicholl, Timothy H., Reverse mathematics, computability, and partitions of trees, this Journal, vol. 74 (2009), no. 1, pp. 201–215.Google Scholar
Corduan, Jared, Groszek, Marcia J., and Mileti, Joseph R., Reverse mathematics and Ramsey’s property for trees, this Journal, vol. 75 (2010), no. 3, pp. 945–954.Google Scholar
Friedman, Harvey, Some systems of second order arithmetic and their use, Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), Vol. 1, 1975, pp. 235–242.Google Scholar
Gasarch, William and Hirst, Jeffry L., Reverse mathematics and recursive graph theory. Mathematical Logic Quarterly. vol. 44 (1998), no. 4, pp. 465–473.CrossRefGoogle Scholar
Groszek, Marcia J., Mytilinaios, Michael E., and Slaman, Theodore A., The Sacks density theorem and Σ2-bounding, this Journal, vol. 61 (1996), no. 2, pp. 450–467.Google Scholar
Groszek, Marcia J. and Slaman, Theodore A., On Turing reducibility, 1994, preprint.Google Scholar
Hájek, Petr, Interpretability and fragments of arithmetic, Arithmetic, proof theory, and computational complexity, 1993, pp. 185–196.CrossRefGoogle Scholar
Hájek, Petr, and Pudlák, Pavel, Metamathematics of First-Order Arithmetic. Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998.Google Scholar
Hirst, Jeffry L., Marriage theorems and reverse mathematics, Logic and computation (Pittsburgh, PA, 1987), 1990, pp. 181–196.CrossRefGoogle Scholar
Jockusch, Carl G. Jr., Degrees of functions with no fixed points. Logic, Methodology and Philosophy of Science VIII, (1989), pp. 191–201.Google Scholar
Jockusch, Carl G. Jr., and Soare, Robert I., ${\rm{\Pi }}_1^0$classes and degrees of theories. Transactions of the American Mathematical Society, vol. 173 (1972), pp. 33–56.Google Scholar
Mytilinaios, Michael E., Finite injury and Σ1-induction, this Journal, vol. 54 (1989), no. 1, pp. 38–49.Google Scholar
Schmerl, James H., Graph coloring and reverse mathematics. Mathematical Logic Quarterly, vol. 46 (2000), no. 4, pp. 543–548.3.0.CO;2-E>CrossRefGoogle Scholar
Schmerl, James H., Reverse mathematics and graph coloring: eliminating diagonalization, Reverse mathematics 2001, 2005, pp. 331–348.Google Scholar
Simpson, Stephen G., Why the recursion theorists ought to thank me, 2001.Google Scholar
Simpson, Stephen G., Subsystems of Second Order Arithmetic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Slaman, Theodore A., Σn-Bounding and Δn-Induction. Proceedings of the American Mathematical Society, vol. 132 (2004), no. 8, pp. 2449–2456.CrossRefGoogle Scholar
Slaman, Theodore A. and Hugh Woodin, W., Σ1-Collection and the finite injury priority method. Mathematical logic and applications, 1989, 178–188.CrossRefGoogle Scholar
Soare, Robert I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar
Yu, Xiaokang and Simpson, Stephen G., Measure theory and weak König’s lemma. Archive for Mathematical Logic, vol. 30 (1990), no. 3, pp. 171–180.CrossRefGoogle Scholar