Article contents
Combinatorial and recursive aspects of the automorphism group of the countable atomless Boolean algebra
Published online by Cambridge University Press: 12 March 2014
Abstract
Given an admissible indexing φ of the countable atomless Boolean algebra ℬ, an automorphism F of ℬ is said to be recursively presented (relative to φ) if there exists a recursive function p ϵ Sym(ω) such that F ∘ φ = φ ∘ p. Our key result on recursiveness: Both the subset of Aut(ℬ) consisting of all those automorphisms which are recursively presented relative to some indexing, and its complement, the set of all “totally nonrecursive” automorphisms, are uncountable.
This arises as a consequence of the following combinatorial investigations: (1) A comparison of the cycle structures of ƒ and 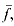 , where ƒ is a permutation of some free basis of ℬ and
, where ƒ is a permutation of some free basis of ℬ and 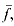 is the automorphism of ℬ induced by ƒ.(2) An explicit description of the permutations of ω whose conjugacy classes in Sym(ω) are (a) uncountable, (b) countably infinite, and (c) finite.
is the automorphism of ℬ induced by ƒ.(2) An explicit description of the permutations of ω whose conjugacy classes in Sym(ω) are (a) uncountable, (b) countably infinite, and (c) finite.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1986
References
REFERENCES
- 1
- Cited by


