Article contents
Coinductive ℵ0-categorical theories
Published online by Cambridge University Press: 12 March 2014
Extract
Let L be a countable language which contains only constant and relation symbols but no function symbols. All theories considered here will be L-theories. A theory is coinductive if it can be axiomatized by a set of ∃∀ sentences, and a structure is coinductive if its theory is.
The object of this paper is to show that coinductive ℵ0-categorical structures are especially simple. First, they are ω-stable with Morley rank ≤ 1; and second, they have simple algebraic closures, by which is meant that the algebraic closure of the union of two sets is the union of their algebraic closures. While these two properties do not characterize coinductive ℵ0-categorical structures, they do characterize those structures which are cellular.
We will say that a countable structure 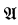 is cellular if there is a finite subset A0 ⊆ A and there are equivalence relations E and F on A∖A0 such that the following hold:
is cellular if there is a finite subset A0 ⊆ A and there are equivalence relations E and F on A∖A0 such that the following hold:
(1) There are only finitely many E-classes.
(2) If C is an E-class and D an F-class, then ∣C ∩ D ∣ = 1.
(3) If a0, a1, …, ak − 1, b0, b1, …, bk − 1 Є A, then 〈a0, a1, …,ak − 1〉 and 〈b0,b1, …, bk − 1〉, satisfy the same quantifier-free formulas provided that:
(a) if i < k and either ai Є A0 or bi Є A0, then ai = bi;
(b) if i < k, then ai; and bi are E-equivalent; and
(c) if i, j < k, then ai; is F-equivalent to aj if bj is F-equivalent to bj.
The main result of this paper is the following theorem.
Theorem 1. If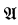 is coinductive and ℵ0-categorical, then
is coinductive and ℵ0-categorical, then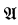 is cellular.
is cellular.
The results of this paper were obtained independently of similar results obtained by Lachlan which can be found in [4] and [5]. The proofs here are quite different.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
REFERENCES
- 7
- Cited by


