Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cardona, Miguel A.
and
Mejía, Diego A.
2019.
On cardinal characteristics of Yorioka ideals.
Mathematical Logic Quarterly,
Vol. 65,
Issue. 2,
p.
170.
Brendle, Jörg
Cardona, Miguel A.
and
Mejía, Diego A.
2021.
Filter-linkedness and its effect on preservation of cardinal characteristics.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 1,
p.
102856.
Goldstern, Martin
Kellner, Jakob
Mejía, Diego A.
and
Shelah, Saharon
2021.
Preservation of splitting families and cardinal characteristics of the continuum.
Israel Journal of Mathematics,
Vol. 246,
Issue. 1,
p.
73.
Goldstern, Martin
and
Klausner, Lukas Daniel
2021.
Cichoń’s diagram and localisation cardinals.
Archive for Mathematical Logic,
Vol. 60,
Issue. 3-4,
p.
343.
Guzmán, Osvaldo
and
Kalajdzievski, Damjan
2021.
The ultrafilter and almost disjointness numbers.
Advances in Mathematics,
Vol. 386,
Issue. ,
p.
107805.
Guzmán, Osvaldo
and
Hrušák, Michael
2022.
MAD families and strategically bounding forcings.
European Journal of Mathematics,
Vol. 8,
Issue. 1,
p.
309.
Guzmán, O.
Hrušák, M.
Rodrigues, V.O.
Todorčević, S.
and
Tomita, A.H.
2022.
Maximal almost disjoint families and pseudocompactness of hyperspaces.
Topology and its Applications,
Vol. 305,
Issue. ,
p.
107872.
CRUZ-CHAPITAL, JORGE A.
FISCHER, VERA
GUZMÁN, OSVALDO
and
ŠUPINA, JAROSLAV
2023.
PARTITION FORCING AND INDEPENDENT FAMILIES.
The Journal of Symbolic Logic,
Vol. 88,
Issue. 4,
p.
1590.
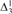 ${\rm{\Delta }}_3^1$ well-order of the reals.
${\rm{\Delta }}_3^1$ well-order of the reals.

