Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T01:56:03.675Z Has data issue: false hasContentIssue false
  • English
  • Français

COHERENT EXTENSION OF PARTIAL AUTOMORPHISMS, FREE AMALGAMATION AND AUTOMORPHISM GROUPS

Published online by Cambridge University Press:  06 May 2019

DAOUD SINIORA  and
SŁAWOMIR SOLECKI
DAOUD SINIORA
Affiliation:
DEPARTMENT OF MATHEMATICS AND ACTUARIAL SCIENCE THE AMERICAN UNIVERSITY IN CAIRO AUC AVENUE, PO BOX 74 NEW CAIRO 11835, EGYPT E-mail: [email protected]
SŁAWOMIR SOLECKI
Affiliation:
DEPARTMENT OF MATHEMATICS CORNELL UNIVERSITY 310 MALOTT HALL ITHACA, NY14853, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give strengthened versions of the Herwig–Lascar and Hodkinson–Otto extension theorems for partial automorphisms of finite structures. Such strengthenings yield several combinatorial and group-theoretic consequences for homogeneous structures. For instance, we establish a coherent form of the extension property for partial automorphisms for certain Fraïssé classes. We deduce from these results that the isometry group of the rational Urysohn space, the automorphism group of the Fraïssé limit of any Fraïssé class that is the class of all 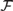${\cal F}$-free structures (in the Herwig–Lascar sense), and the automorphism group of any free homogeneous structure over a finite relational language all contain a dense locally finite subgroup. We also show that any free homogeneous structure admits ample generics.

Keywords

Primary 03C1303C1522F2020B27Secondary 08A3554H11extension property for partial automorphismscoherent EPPAFraïssé limitsample genericshomogeneous structures
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 1 , March 2020 , pp. 199 - 223
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bhattacharjee, M. and Macpherson, D., A locally finite dense group acting on the random graph. Forum Mathematicum, vol. 17 (2005), no. 3, pp. 513–517.CrossRefGoogle Scholar
Cameron, P. J., The random graph, The mathematics of Paul Erdös, II (Graham, R., Nesetril, J., and Butler, S., editors), Algorithms Combin, vol. 14, Springer, Berlin, 1997, pp. 333–351.CrossRefGoogle Scholar
Henson, C. W., Countable homogeneous relational structures and ${\aleph _0}$-categorical theories, this Journal, vol. 37 (1972), pp. 494–500.Google Scholar
Herwig, B., Extending partial isomorphisms for the small index property of many ω-categorical structures. Israel Journal of Mathematics, vol. 107 (1998), no. 1, pp. 93–123.CrossRefGoogle Scholar
Herwig, B. and Lascar, D., Extending partial automorphisms and the profinite topology on free groups. American Mathematical Society, vol. 352 (1999), pp. 1985–2021.CrossRefGoogle Scholar
Hodges, W., Hodkinson, I., Lascar, D., and Shelah, S., The small index property for ω-stable, ω-categorical structures and for the random graph. Journal of the London Mathematical Society, vol. 2 (1993), no. 2, pp. 204–218.CrossRefGoogle Scholar
Hodkinson, I. and Otto, M., Finite conformal hypergraph covers and Gaifman cliques in finite structures. The Bulletin of Symbolic Logic, vol. 9 (2003), no. 3, pp. 387–405.CrossRefGoogle Scholar
Ivanov, A., Automorphisms of homogeneous structures. Notre Dame Journal of Formal Logic, vol. 46 (2005), no. 4, pp. 419–424.CrossRefGoogle Scholar
Ivanov, A., Strongly bounded automorphism groups. Colloquium Mathematicum, vol. 105 (2006), no. 1, pp. 57–67.CrossRefGoogle Scholar
Kechris, A. S. and Rosendal, C., Turbulence, amalgamation, and generic automorphisms of homogeneous structures. Proceedings of the London Mathematical Society, vol. 94 (2007), no. 2, pp. 302–350.CrossRefGoogle Scholar
Mackey, G. W., Ergodic theory and virtual groups. Mathematische Annalen, vol. 166 (1966), pp. 187–207.CrossRefGoogle Scholar
Macpherson, D., A survey of homogeneous structures. Discrete Mathematics, vol. 311 (2011), no. 15, pp. 1599–1634.CrossRefGoogle Scholar
Macpherson, D. and Tent, K., Simplicity of some automorphism groups. Journal of Algebra, vol. 342 (2011), no. 1, pp. 40–52.CrossRefGoogle Scholar
Macpherson, D. and Thomas, S., Comeagre conjugacy classes and free products with amalgamation. Discrete Mathematics, vol. 291 (2005), no. 1, pp. 135–142.CrossRefGoogle Scholar
Rosendal, C., Finitely approximable groups and actions part I: The Ribes-Zalesskiĭ property, this Journal, vol. 76 (2011), no. 4, pp. 1297–1306.Google Scholar
Siniora, D., Automorphism groups of homogeneous structures. Ph.D. thesis, University of Leeds, 2017.Google Scholar
Solecki, S., Extending partial isometries. Israel Journal of Mathematics, vol. 150 (2005), no. 1, pp. 315–331.CrossRefGoogle Scholar
Thomas, S.. Reducts of random hypergraphs. Annals of Pure and Applied Logic, vol. 80 (1996), no. 2, pp. 165–193.CrossRefGoogle Scholar